Dif-MAML: Decentralized Multi-Agent Meta-Learning

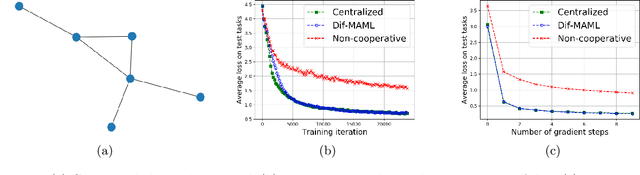
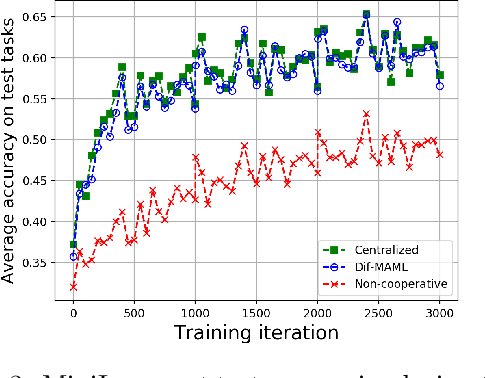
The objective of meta-learning is to exploit the knowledge obtained from observed tasks to improve adaptation to unseen tasks. As such, meta-learners are able to generalize better when they are trained with a larger number of observed tasks and with a larger amount of data per task. Given the amount of resources that are needed, it is generally difficult to expect the tasks, their respective data, and the necessary computational capacity to be available at a single central location. It is more natural to encounter situations where these resources are spread across several agents connected by some graph topology. The formalism of meta-learning is actually well-suited to this decentralized setting, where the learner would be able to benefit from information and computational power spread across the agents. Motivated by this observation, in this work, we propose a cooperative fully-decentralized multi-agent meta-learning algorithm, referred to as Diffusion-based MAML or Dif-MAML. Decentralized optimization algorithms are superior to centralized implementations in terms of scalability, avoidance of communication bottlenecks, and privacy guarantees. The work provides a detailed theoretical analysis to show that the proposed strategy allows a collection of agents to attain agreement at a linear rate and to converge to a stationary point of the aggregate MAML objective even in non-convex environments. Simulation results illustrate the theoretical findings and the superior performance relative to the traditional non-cooperative setting.

A Multi-Agent Primal-Dual Strategy for Composite Optimization over Distributed Features

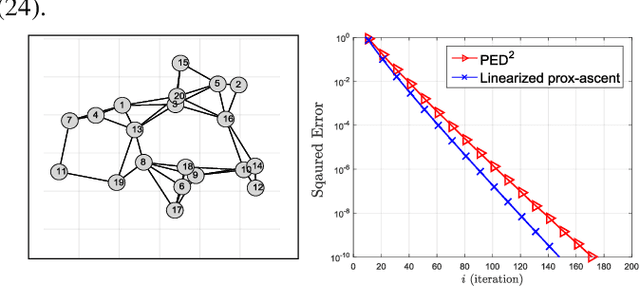
This work studies multi-agent sharing optimization problems with the objective function being the sum of smooth local functions plus a convex (possibly non-smooth) function coupling all agents. This scenario arises in many machine learning and engineering applications, such as regression over distributed features and resource allocation. We reformulate this problem into an equivalent saddle-point problem, which is amenable to decentralized solutions. We then propose a proximal primal-dual algorithm and establish its linear convergence to the optimal solution when the local functions are strongly-convex. To our knowledge, this is the first linearly convergent decentralized algorithm for multi-agent sharing problems with a general convex (possibly non-smooth) coupling function.

Logical Team Q-learning: An approach towards factored policies in cooperative MARL

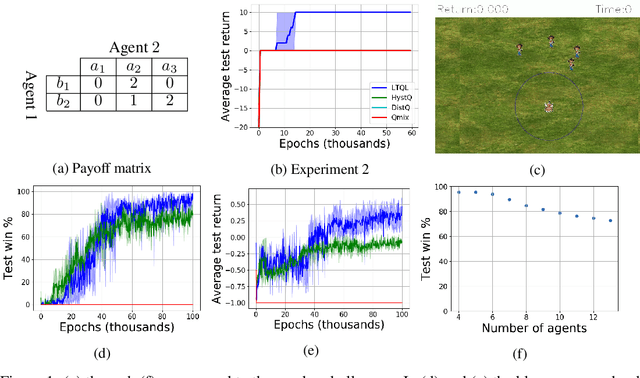
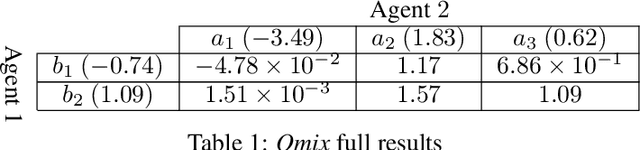
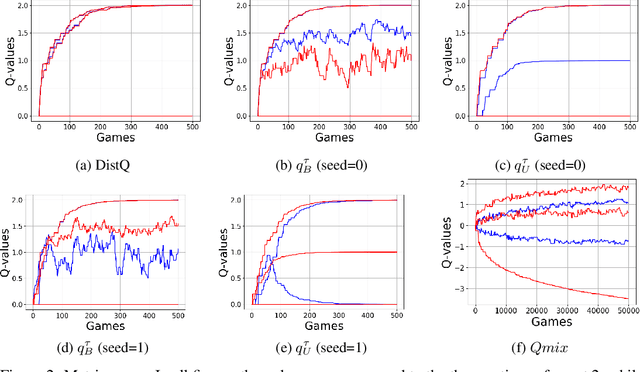
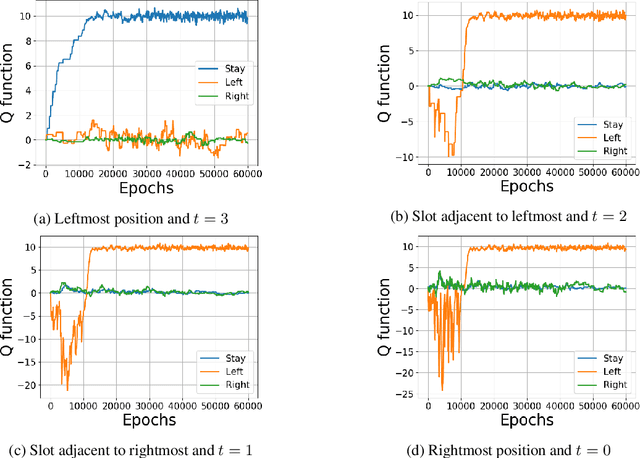
We address the challenge of learning factored policies in cooperative MARL scenarios. In particular, we consider the situation in which a team of agents collaborates to optimize a common cost. Our goal is to obtain factored policies that determine the individual behavior of each agent so that the resulting joint policy is optimal. In this work we make contributions to both the dynamic programming and reinforcement learning settings. In the dynamic programming case we provide a number of lemmas that prove the existence of such factored policies and we introduce an algorithm (along with proof of convergence) that provably leads to them. Then we introduce tabular and deep versions of Logical Team Q-learning, which is a stochastic version of the algorithm for the RL case. We conclude the paper by providing experiments that illustrate the claims.

Tracking Performance of Online Stochastic Learners

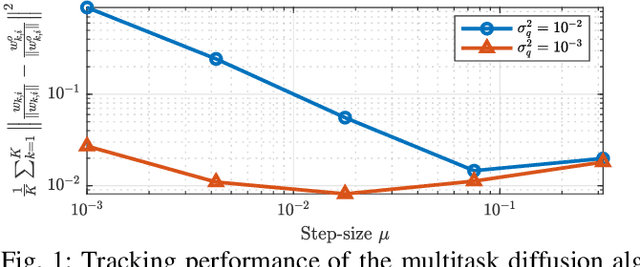
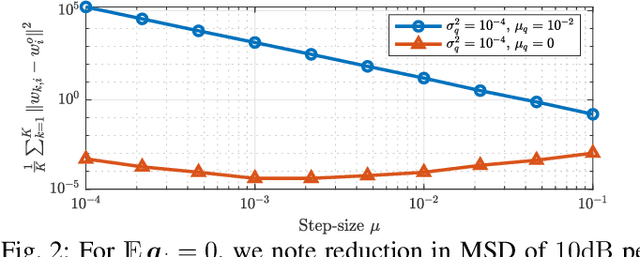
The utilization of online stochastic algorithms is popular in large-scale learning settings due to their ability to compute updates on the fly, without the need to store and process data in large batches. When a constant step-size is used, these algorithms also have the ability to adapt to drifts in problem parameters, such as data or model properties, and track the optimal solution with reasonable accuracy. Building on analogies with the study of adaptive filters, we establish a link between steady-state performance derived under stationarity assumptions and the tracking performance of online learners under random walk models. The link allows us to infer the tracking performance from steady-state expressions directly and almost by inspection.

Second-Order Guarantees in Centralized, Federated and Decentralized Nonconvex Optimization

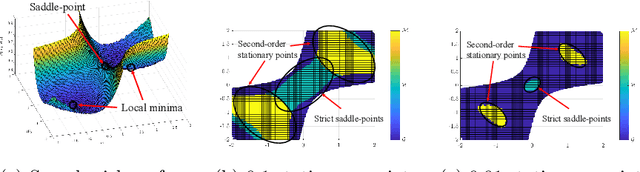
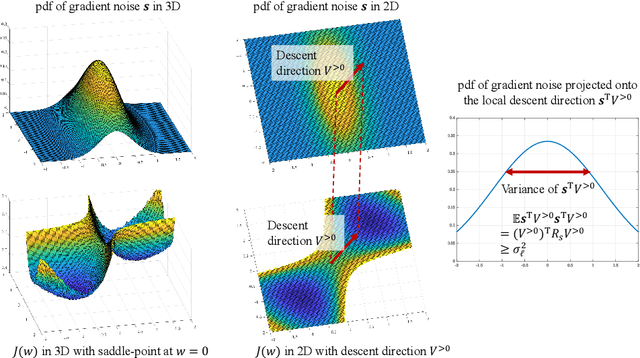
Rapid advances in data collection and processing capabilities have allowed for the use of increasingly complex models that give rise to nonconvex optimization problems. These formulations, however, can be arbitrarily difficult to solve in general, in the sense that even simply verifying that a given point is a local minimum can be NP-hard [1]. Still, some relatively simple algorithms have been shown to lead to surprisingly good empirical results in many contexts of interest. Perhaps the most prominent example is the success of the backpropagation algorithm for training neural networks. Several recent works have pursued rigorous analytical justification for this phenomenon by studying the structure of the nonconvex optimization problems and establishing that simple algorithms, such as gradient descent and its variations, perform well in converging towards local minima and avoiding saddle-points. A key insight in these analyses is that gradient perturbations play a critical role in allowing local descent algorithms to efficiently distinguish desirable from undesirable stationary points and escape from the latter. In this article, we cover recent results on second-order guarantees for stochastic first-order optimization algorithms in centralized, federated, and decentralized architectures.

Dynamic Federated Learning

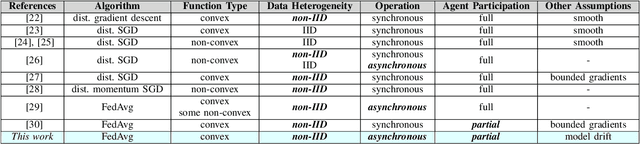
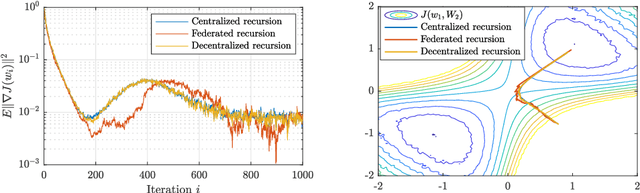
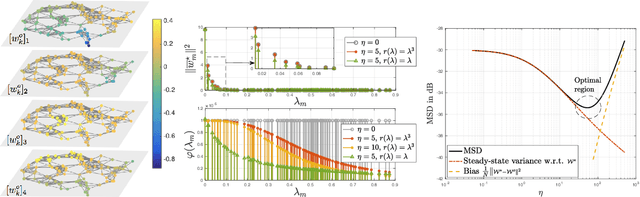
Federated learning has emerged as an umbrella term for centralized coordination strategies in multi-agent environments. While many federated learning architectures process data in an online manner, and are hence adaptive by nature, most performance analyses assume static optimization problems and offer no guarantees in the presence of drifts in the problem solution or data characteristics. We consider a federated learning model where at every iteration, a random subset of available agents perform local updates based on their data. Under a non-stationary random walk model on the true minimizer for the aggregate optimization problem, we establish that the performance of the architecture is determined by three factors, namely, the data variability at each agent, the model variability across all agents, and a tracking term that is inversely proportional to the learning rate of the algorithm. The results clarify the trade-off between convergence and tracking performance.

Multitask learning over graphs

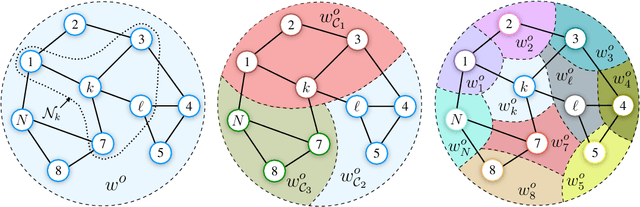
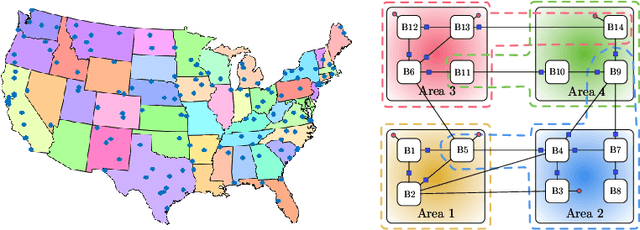
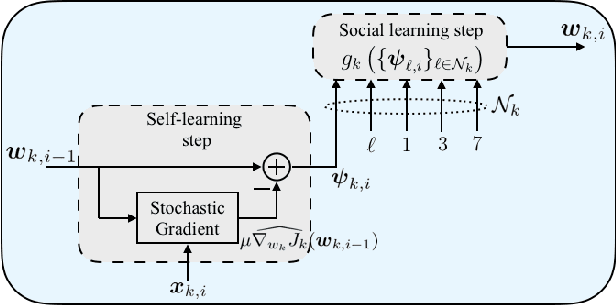
The problem of learning simultaneously several related tasks has received considerable attention in several domains, especially in machine learning with the so-called multitask learning problem or learning to learn problem [1], [2]. Multitask learning is an approach to inductive transfer learning (using what is learned for one problem to assist in another problem) and helps improve generalization performance relative to learning each task separately by using the domain information contained in the training signals of related tasks as an inductive bias. Several strategies have been derived within this community under the assumption that all data are available beforehand at a fusion center. However, recent years have witnessed an increasing ability to collect data in a distributed and streaming manner. This requires the design of new strategies for learning jointly multiple tasks from streaming data over distributed (or networked) systems. This article provides an overview of multitask strategies for learning and adaptation over networks. The working hypothesis for these strategies is that agents are allowed to cooperate with each other in order to learn distinct, though related tasks. The article shows how cooperation steers the network limiting point and how different cooperation rules allow to promote different task relatedness models. It also explains how and when cooperation over multitask networks outperforms non-cooperative strategies.

Inverse Graph Learning over Optimization Networks

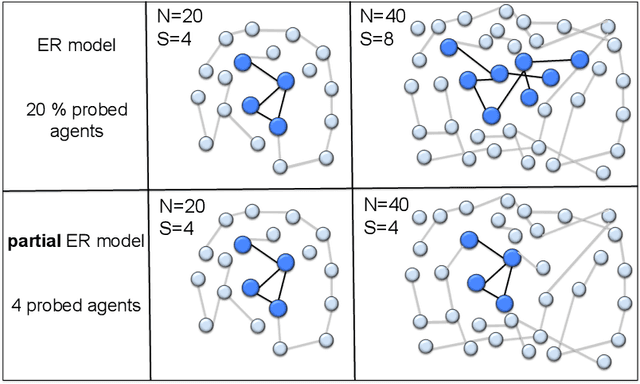
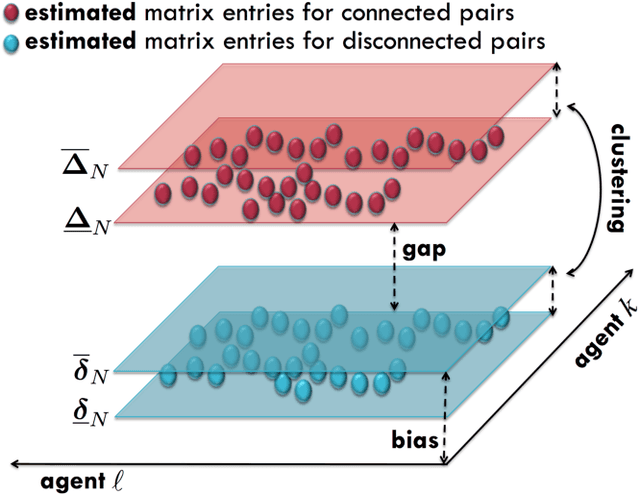
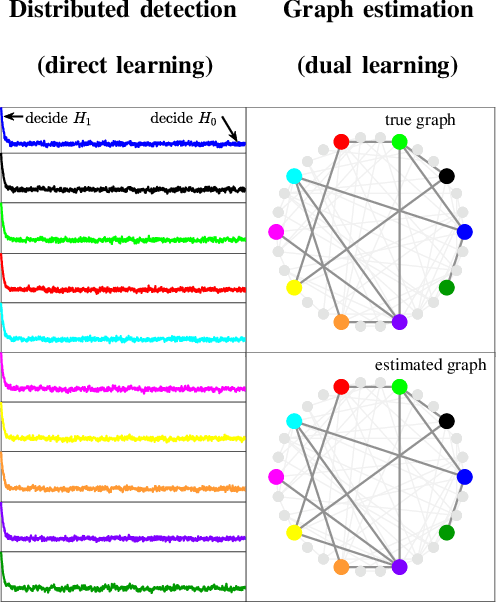
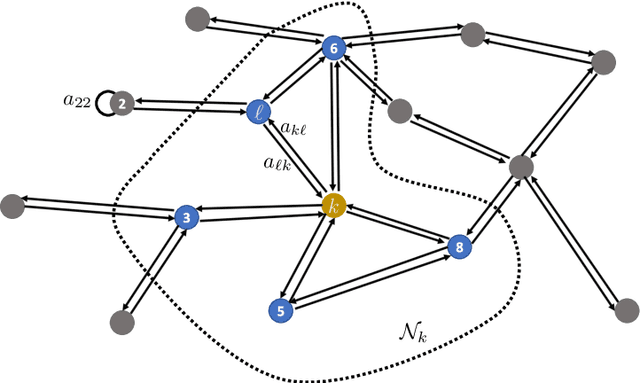
Many inferential and learning tasks can be accomplished efficiently by means of distributed optimization algorithms where the network topology plays a critical role in driving the local interactions among neighboring agents. There is a large body of literature examining the effect of the graph structure on the performance of optimization strategies. In this article, we examine the inverse problem and consider the reverse question: How much information does observing the behavior at the nodes convey about the underlying network structure used for optimization? Over large-scale networks, the difficulty of addressing such inverse questions (or problems) is compounded by the fact that usually only a limited portion of nodes can be probed, giving rise to a second important question: Despite the presence of several unobserved nodes, are partial and local observations still sufficient to discover the graph linking the probed nodes? The article surveys recent advances on this inverse learning problem and related questions. Examples of applications are provided to illustrate how the interplay between graph learning and distributed optimization arises in practice, e.g., in cognitive engineered systems such as distributed detection, or in other real-world problems such as the mechanism of opinion formation over social networks and the mechanism of coordination in biological networks. A unifying framework for examining the reconstruction error will be described, which allows to devise and examine various estimation strategies enabling successful graph learning. The relevance of specific network attributes, such as sparsity versus density of connections, and node degree concentration, is discussed in relation to the topology inference goal. It is shown how universal (i.e., data-driven) clustering algorithms can be exploited to solve the graph learning problem.

Network Classifiers With Output Smoothing

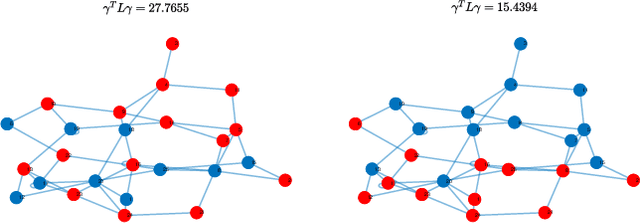
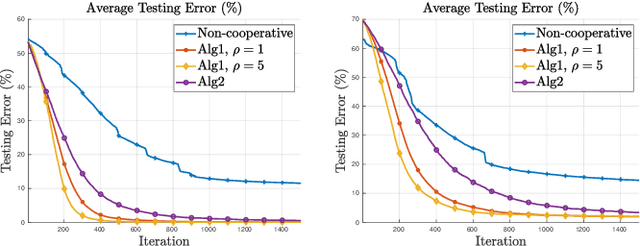
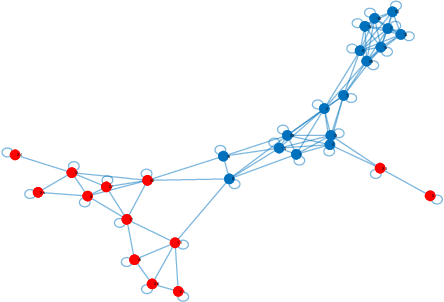
This work introduces two strategies for training network classifiers with heterogeneous agents. One strategy promotes global smoothing over the graph and a second strategy promotes local smoothing over neighbourhoods. It is assumed that the feature sizes can vary from one agent to another, with some agents observing insufficient attributes to be able to make reliable decisions on their own. As a result, cooperation with neighbours is necessary. However, due to the fact that the feature dimensions are different across the agents, their classifier dimensions will also be different. This means that cooperation cannot rely on combining the classifier parameters. We instead propose smoothing the outputs of the classifiers, which are the predicted labels. By doing so, the dynamics that describes the evolution of the network classifier becomes more challenging than usual because the classifier parameters end up appearing as part of the regularization term as well. We illustrate performance by means of computer simulations.

Linear Speedup in Saddle-Point Escape for Decentralized Non-Convex Optimization

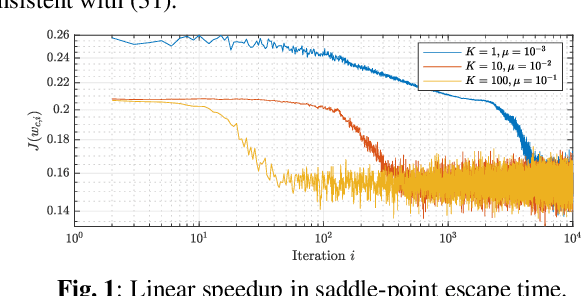
Under appropriate cooperation protocols and parameter choices, fully decentralized solutions for stochastic optimization have been shown to match the performance of centralized solutions and result in linear speedup (in the number of agents) relative to non-cooperative approaches in the strongly-convex setting. More recently, these results have been extended to the pursuit of first-order stationary points in non-convex environments. In this work, we examine in detail the dependence of second-order convergence guarantees on the spectral properties of the combination policy for non-convex multi agent optimization. We establish linear speedup in saddle-point escape time in the number of agents for symmetric combination policies and study the potential for further improvement by employing asymmetric combination weights. The results imply that a linear speedup can be expected in the pursuit of second-order stationary points, which exclude local maxima as well as strict saddle-points and correspond to local or even global minima in many important learning settings.