Noninvasive Intracranial Pressure Estimation Using Subspace System Identification and Bespoke Machine Learning Algorithms: A Learning-to-Rank Approach

Objective: Accurate noninvasive estimation of intracranial pressure (ICP) remains a major challenge in critical care. We developed a bespoke machine learning algorithm that integrates system identification and ranking-constrained optimization to estimate mean ICP from noninvasive signals. Methods: A machine learning framework was proposed to obtain accurate mean ICP values using arbitrary noninvasive signals. The subspace system identification algorithm is employed to identify cerebral hemodynamics models for ICP simulation using arterial blood pressure (ABP), cerebral blood velocity (CBv), and R-wave to R-wave interval (R-R interval) signals in a comprehensive database. A mapping function to describe the relationship between the features of noninvasive signals and the estimation errors is learned using innovative ranking constraints through convex optimization. Patients across multiple clinical settings were randomly split into testing and training datasets for performance evaluation of the mapping function. Results: The results indicate that about 31.88% of testing entries achieved estimation errors within 2 mmHg and 34.07% of testing entries between 2 mmHg to 6 mmHg from the nonlinear mapping with constraints. Conclusion: Our results demonstrate the feasibility of the proposed noninvasive ICP estimation approach. Significance: Further validation and technical refinement are required before clinical deployment, but this work lays the foundation for safe and broadly accessible ICP monitoring in patients with acute brain injury and related conditions.

Regularized Diffusion Adaptation via Conjugate Smoothing

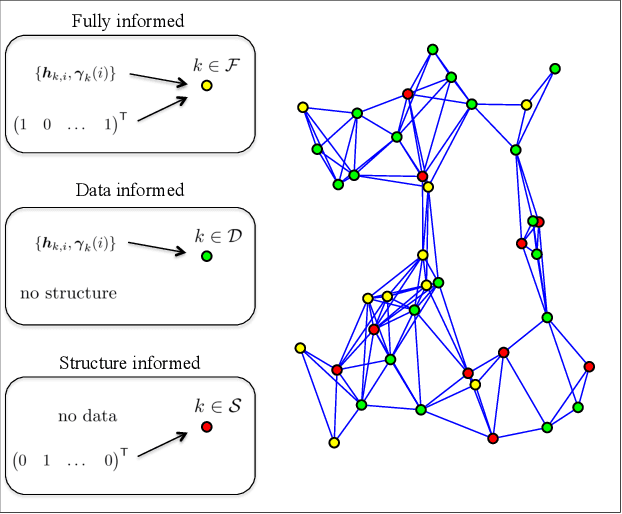
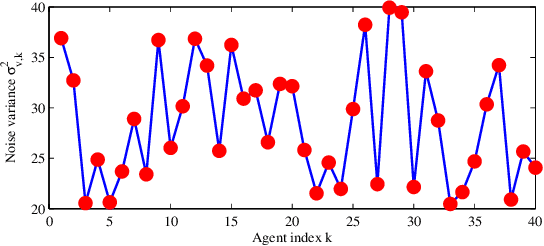
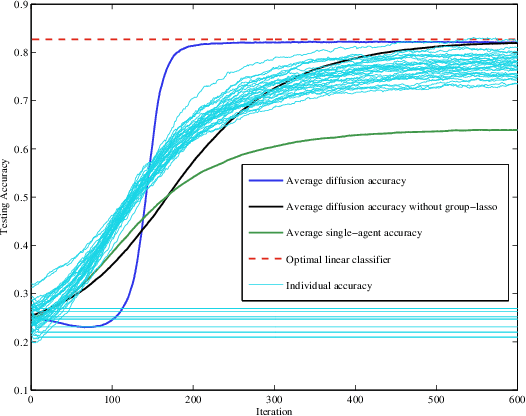
The purpose of this work is to develop and study a distributed strategy for Pareto optimization of an aggregate cost consisting of regularized risks. Each risk is modeled as the expectation of some loss function with unknown probability distribution while the regularizers are assumed deterministic, but are not required to be differentiable or even continuous. The individual, regularized, cost functions are distributed across a strongly-connected network of agents and the Pareto optimal solution is sought by appealing to a multi-agent diffusion strategy. To this end, the regularizers are smoothed by means of infimal convolution and it is shown that the Pareto solution of the approximate, smooth problem can be made arbitrarily close to the solution of the original, non-smooth problem. Performance bounds are established under conditions that are weaker than assumed before in the literature, and hence applicable to a broader class of adaptation and learning problems.