An active inference model of car following: Advantages and applications

Driver process models play a central role in the testing, verification, and development of automated and autonomous vehicle technologies. Prior models developed from control theory and physics-based rules are limited in automated vehicle applications due to their restricted behavioral repertoire. Data-driven machine learning models are more capable than rule-based models but are limited by the need for large training datasets and their lack of interpretability, i.e., an understandable link between input data and output behaviors. We propose a novel car following modeling approach using active inference, which has comparable behavioral flexibility to data-driven models while maintaining interpretability. We assessed the proposed model, the Active Inference Driving Agent (AIDA), through a benchmark analysis against the rule-based Intelligent Driver Model, and two neural network Behavior Cloning models. The models were trained and tested on a real-world driving dataset using a consistent process. The testing results showed that the AIDA predicted driving controls significantly better than the rule-based Intelligent Driver Model and had similar accuracy to the data-driven neural network models in three out of four evaluations. Subsequent interpretability analyses illustrated that the AIDA's learned distributions were consistent with driver behavior theory and that visualizations of the distributions could be used to directly comprehend the model's decision making process and correct model errors attributable to limited training data. The results indicate that the AIDA is a promising alternative to black-box data-driven models and suggest a need for further research focused on modeling driving style and model training with more diverse datasets.

Understanding Expertise through Demonstrations: A Maximum Likelihood Framework for Offline Inverse Reinforcement Learning

Offline inverse reinforcement learning (Offline IRL) aims to recover the structure of rewards and environment dynamics that underlie observed actions in a fixed, finite set of demonstrations from an expert agent. Accurate models of expertise in executing a task has applications in safety-sensitive applications such as clinical decision making and autonomous driving. However, the structure of an expert's preferences implicit in observed actions is closely linked to the expert's model of the environment dynamics (i.e. the ``world''). Thus, inaccurate models of the world obtained from finite data with limited coverage could compound inaccuracy in estimated rewards. To address this issue, we propose a bi-level optimization formulation of the estimation task wherein the upper level is likelihood maximization based upon a conservative model of the expert's policy (lower level). The policy model is conservative in that it maximizes reward subject to a penalty that is increasing in the uncertainty of the estimated model of the world. We propose a new algorithmic framework to solve the bi-level optimization problem formulation and provide statistical and computational guarantees of performance for the associated reward estimator. Finally, we demonstrate that the proposed algorithm outperforms the state-of-the-art offline IRL and imitation learning benchmarks by a large margin, over the continuous control tasks in MuJoCo and different datasets in the D4RL benchmark.

Maximum-Likelihood Inverse Reinforcement Learning with Finite-Time Guarantees

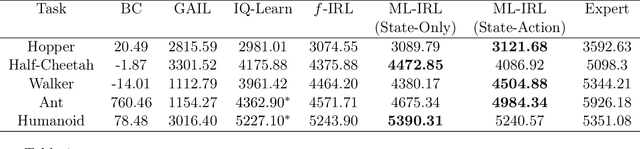
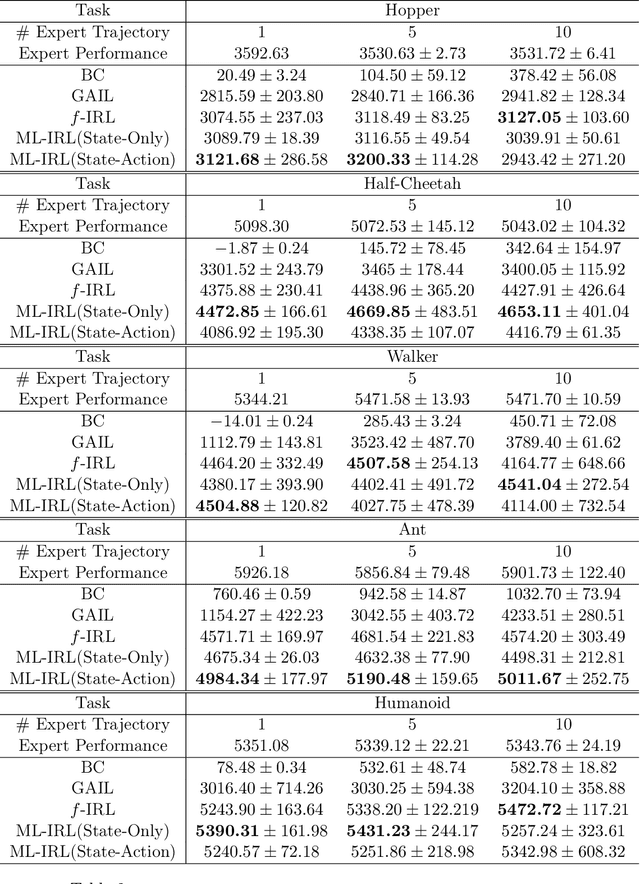
Inverse reinforcement learning (IRL) aims to recover the reward function and the associated optimal policy that best fits observed sequences of states and actions implemented by an expert. Many algorithms for IRL have an inherently nested structure: the inner loop finds the optimal policy given parametrized rewards while the outer loop updates the estimates towards optimizing a measure of fit. For high dimensional environments such nested-loop structure entails a significant computational burden. To reduce the computational burden of a nested loop, novel methods such as SQIL [1] and IQ-Learn [2] emphasize policy estimation at the expense of reward estimation accuracy. However, without accurate estimated rewards, it is not possible to do counterfactual analysis such as predicting the optimal policy under different environment dynamics and/or learning new tasks. In this paper we develop a novel single-loop algorithm for IRL that does not compromise reward estimation accuracy. In the proposed algorithm, each policy improvement step is followed by a stochastic gradient step for likelihood maximization. We show that the proposed algorithm provably converges to a stationary solution with a finite-time guarantee. If the reward is parameterized linearly, we show the identified solution corresponds to the solution of the maximum entropy IRL problem. Finally, by using robotics control problems in MuJoCo and their transfer settings, we show that the proposed algorithm achieves superior performance compared with other IRL and imitation learning benchmarks.

Structural Estimation of Markov Decision Processes in High-Dimensional State Space with Finite-Time Guarantees

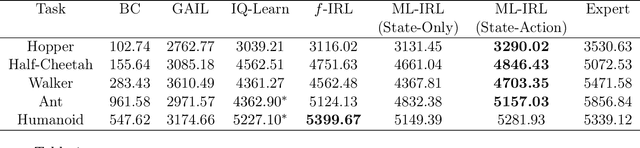
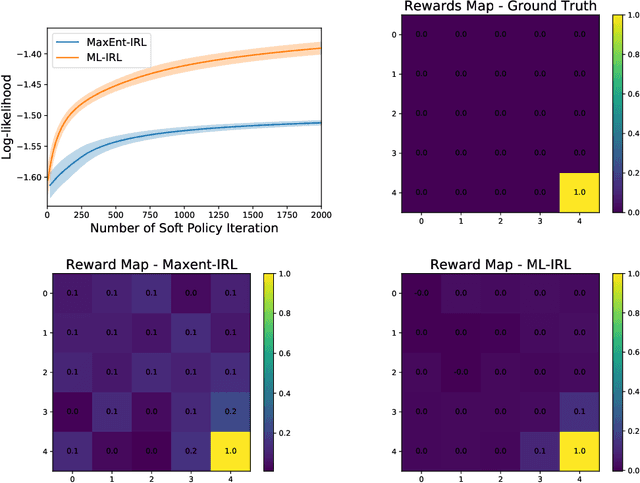
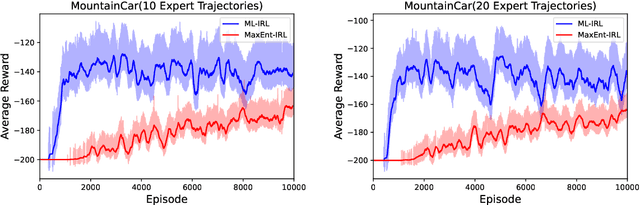
We consider the task of estimating a structural model of dynamic decisions by a human agent based upon the observable history of implemented actions and visited states. This problem has an inherent nested structure: in the inner problem, an optimal policy for a given reward function is identified while in the outer problem, a measure of fit is maximized. Several approaches have been proposed to alleviate the computational burden of this nested-loop structure, but these methods still suffer from high complexity when the state space is either discrete with large cardinality or continuous in high dimensions. Other approaches in the inverse reinforcement learning (IRL) literature emphasize policy estimation at the expense of reduced reward estimation accuracy. In this paper we propose a single-loop estimation algorithm with finite time guarantees that is equipped to deal with high-dimensional state spaces without compromising reward estimation accuracy. In the proposed algorithm, each policy improvement step is followed by a stochastic gradient step for likelihood maximization. We show that the proposed algorithm converges to a stationary solution with a finite-time guarantee. Further, if the reward is parameterized linearly, we show that the algorithm approximates the maximum likelihood estimator sublinearly. Finally, by using robotics control problems in MuJoCo and their transfer settings, we show that the proposed algorithm achieves superior performance compared with other IRL and imitation learning benchmarks.

Learning to Coordinate in Multi-Agent Systems: A Coordinated Actor-Critic Algorithm and Finite-Time Guarantees

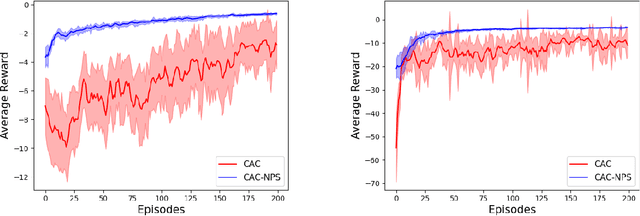
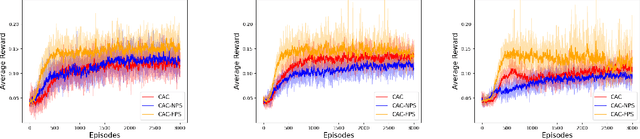
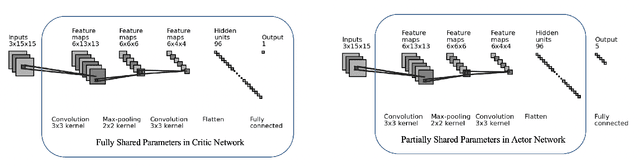
Multi-agent reinforcement learning (MARL) has attracted much research attention recently. However, unlike its single-agent counterpart, many theoretical and algorithmic aspects of MARL have not been well-understood. In this paper, we study the emergence of coordinated behavior by autonomous agents using an actor-critic (AC) algorithm. Specifically, we propose and analyze a class of coordinated actor-critic algorithms (CAC) in which individually parametrized policies have a {\it shared} part (which is jointly optimized among all agents) and a {\it personalized} part (which is only locally optimized). Such kind of {\it partially personalized} policy allows agents to learn to coordinate by leveraging peers' past experience and adapt to individual tasks. The flexibility in our design allows the proposed MARL-CAC algorithm to be used in a {\it fully decentralized} setting, where the agents can only communicate with their neighbors, as well as a {\it federated} setting, where the agents occasionally communicate with a server while optimizing their (partially personalized) local models. Theoretically, we show that under some standard regularity assumptions, the proposed MARL-CAC algorithm requires $\mathcal{O}(\epsilon^{-\frac{5}{2}})$ samples to achieve an $\epsilon$-stationary solution (defined as the solution whose squared norm of the gradient of the objective function is less than $\epsilon$). To the best of our knowledge, this work provides the first finite-sample guarantee for decentralized AC algorithm with partially personalized policies.

Decentralized Riemannian Gradient Descent on the Stiefel Manifold

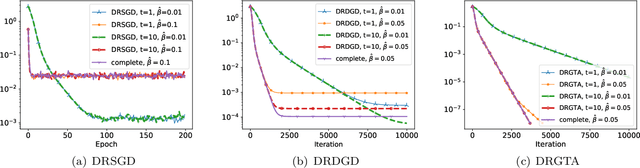
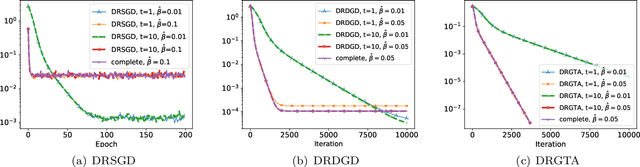
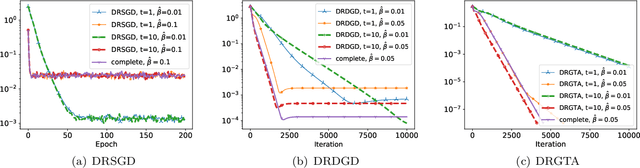
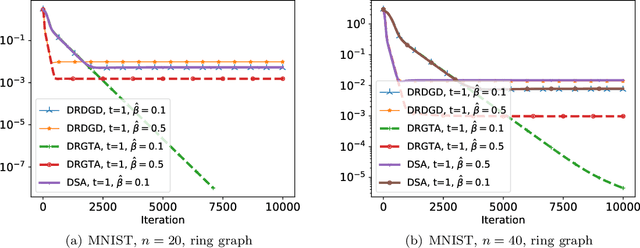
We consider a distributed non-convex optimization where a network of agents aims at minimizing a global function over the Stiefel manifold. The global function is represented as a finite sum of smooth local functions, where each local function is associated with one agent and agents communicate with each other over an undirected connected graph. The problem is non-convex as local functions are possibly non-convex (but smooth) and the Steifel manifold is a non-convex set. We present a decentralized Riemannian stochastic gradient method (DRSGD) with the convergence rate of $\mathcal{O}(1/\sqrt{K})$ to a stationary point. To have exact convergence with constant stepsize, we also propose a decentralized Riemannian gradient tracking algorithm (DRGTA) with the convergence rate of $\mathcal{O}(1/K)$ to a stationary point. We use multi-step consensus to preserve the iteration in the local (consensus) region. DRGTA is the first decentralized algorithm with exact convergence for distributed optimization on Stiefel manifold.

On the Local Linear Rate of Consensus on the Stiefel Manifold

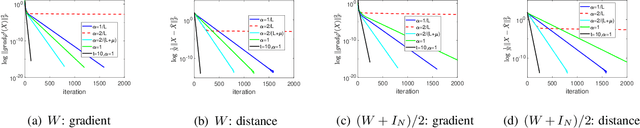
We study the convergence properties of Riemannian gradient method for solving the consensus problem (for an undirected connected graph) over the Stiefel manifold. The Stiefel manifold is a non-convex set and the standard notion of averaging in the Euclidean space does not work for this problem. We propose Distributed Riemannian Consensus on Stiefel Manifold (DRCS) and prove that it enjoys a local linear convergence rate to global consensus. More importantly, this local rate asymptotically scales with the second largest singular value of the communication matrix, which is on par with the well-known rate in the Euclidean space. To the best of our knowledge, this is the first work showing the equality of the two rates. The main technical challenges include (i) developing a Riemannian restricted secant inequality for convergence analysis, and (ii) to identify the conditions (e.g., suitable step-size and initialization) under which the algorithm always stays in the local region.

Dynamic Discrete Choice Estimation with Partially Observable States and Hidden Dynamics

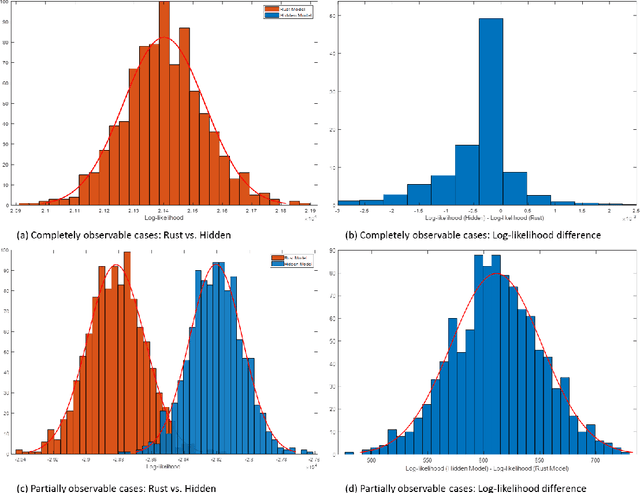
Dynamic discrete choice models are used to estimate the intertemporal preferences of an agent as described by a reward function based upon observable histories of states and implemented actions. However, in many applications, such as reliability and healthcare, the system state is partially observable or hidden (e.g., the level of deterioration of an engine, the condition of a disease), and the decision maker only has access to information imperfectly correlated with the true value of the hidden state. In this paper, we consider the estimation of a dynamic discrete choice model with state variables and system dynamics that are hidden (or partially observed) to both the agent and the modeler, thus generalizing Rust's model to partially observable cases. We analyze the structural properties of the model and prove that this model is still identifiable if the cardinality of the state space, the discount factor, the distribution of random shocks, and the rewards for a given (reference) action are given. We analyze both theoretically and numerically the potential mis-specification errors that may be incurred when Rust's model is improperly used in partially observable settings. We further apply the developed model to a subset of Rust's dataset for bus engine mileage and replacement decisions. The results show that our model can improve model fit as measured by the $\log$-likelihood function by $17.7\%$ and the $\log$-likelihood ratio test shows that our model statistically outperforms Rust's model. Interestingly, our hidden state model also reveals an economically meaningful route assignment behavior in the dataset which was hitherto ignored, i.e. routes with lower mileage are assigned to buses believed to be in worse condition.

Distributed Projected Subgradient Method for Weakly Convex Optimization

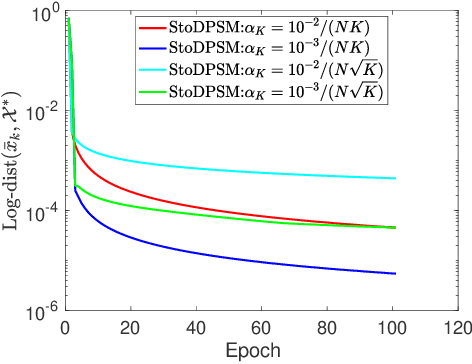
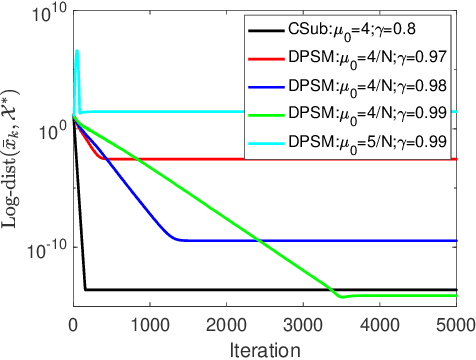
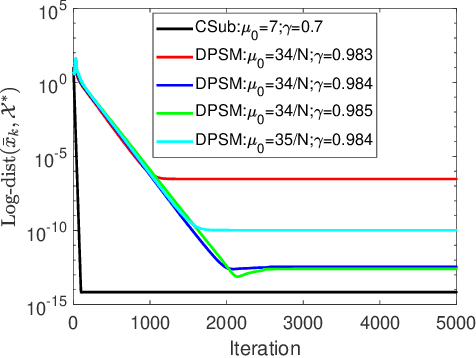
The stochastic subgradient method is a widely-used algorithm for solving large-scale optimization problems arising in machine learning. Often these problems are neither smooth nor convex. Recently, Davis et al. [1-2] characterized the convergence of the stochastic subgradient method for the weakly convex case, which encompasses many important applications (e.g., robust phase retrieval, blind deconvolution, biconvex compressive sensing, and dictionary learning). In practice, distributed implementations of the projected stochastic subgradient method (stoDPSM) are used to speed-up risk minimization. In this paper, we propose a distributed implementation of the stochastic subgradient method with a theoretical guarantee. Specifically, we show the global convergence of stoDPSM using the Moreau envelope stationarity measure. Furthermore, under a so-called sharpness condition, we show that deterministic DPSM (with a proper initialization) converges linearly to the sharp minima, using geometrically diminishing step-size. We provide numerical experiments to support our theoretical analysis.

Distributed Estimation via Network Regularization

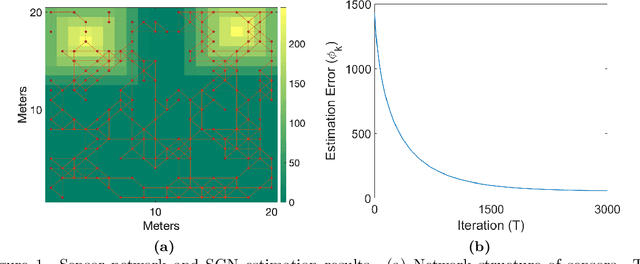
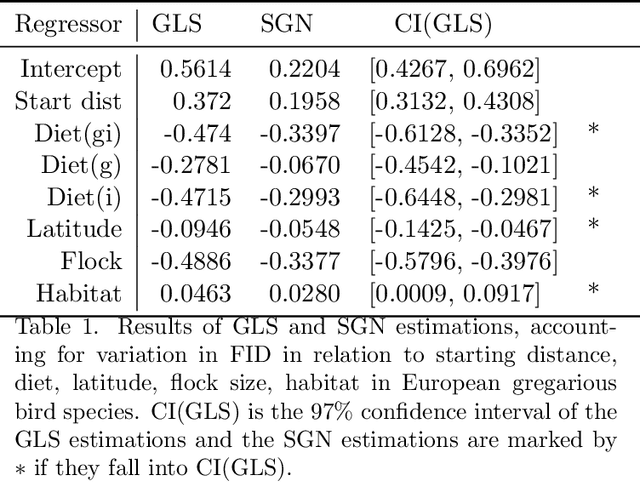
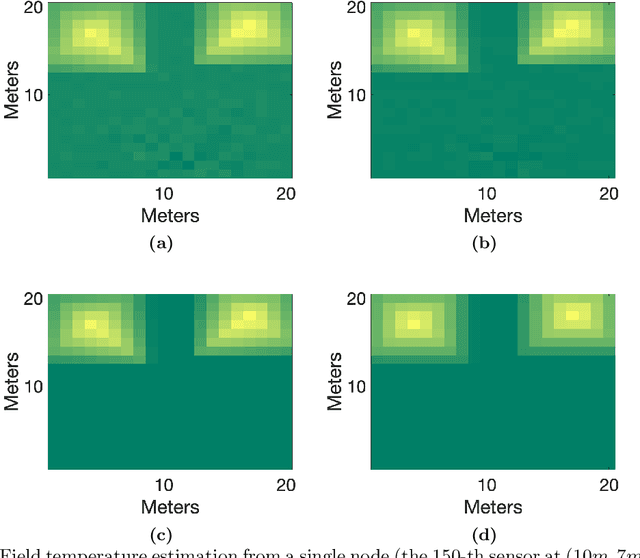
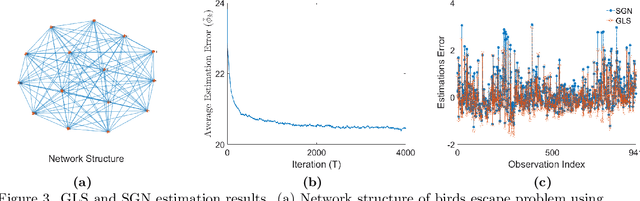
We propose a new method for distributed estimation of a linear model by a network of local learners with heterogeneously distributed datasets. Unlike other ensemble learning methods, in the proposed method, model averaging is done continuously over time in a distributed and asynchronous manner. To ensure robust estimation, a network regularization term which penalizes models with high local variability is used. We provide a finite-time characterization of convergence of the weighted ensemble average and compare this result to centralized estimation. We illustrate the general applicability of the method in two examples: estimation of a Markov random field using wireless sensor networks and modeling prey escape behavior of birds based on a real-world dataset.