Optimizing Mixed Autonomy Traffic Flow With Decentralized Autonomous Vehicles and Multi-Agent RL

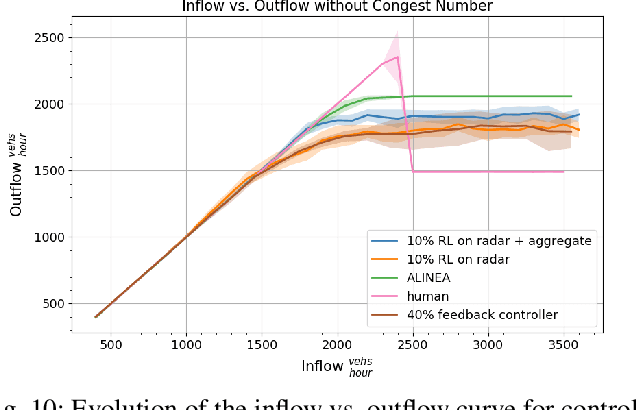
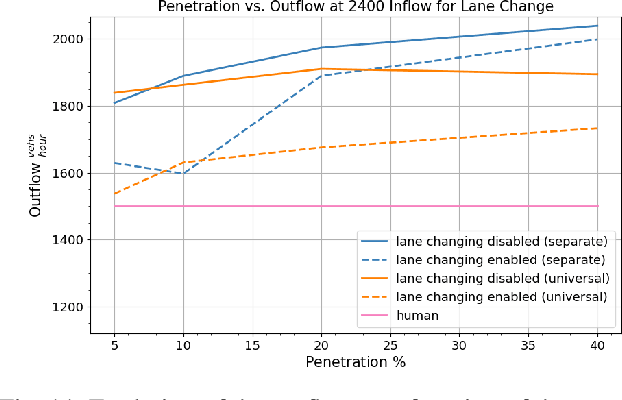
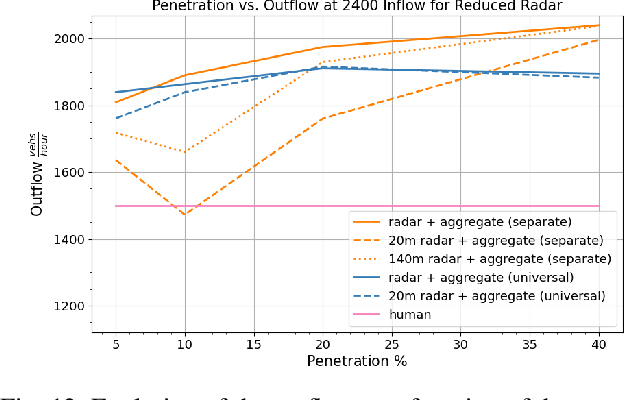
We study the ability of autonomous vehicles to improve the throughput of a bottleneck using a fully decentralized control scheme in a mixed autonomy setting. We consider the problem of improving the throughput of a scaled model of the San Francisco-Oakland Bay Bridge: a two-stage bottleneck where four lanes reduce to two and then reduce to one. Although there is extensive work examining variants of bottleneck control in a centralized setting, there is less study of the challenging multi-agent setting where the large number of interacting AVs leads to significant optimization difficulties for reinforcement learning methods. We apply multi-agent reinforcement algorithms to this problem and demonstrate that significant improvements in bottleneck throughput, from 20\% at a 5\% penetration rate to 33\% at a 40\% penetration rate, can be achieved. We compare our results to a hand-designed feedback controller and demonstrate that our results sharply outperform the feedback controller despite extensive tuning. Additionally, we demonstrate that the RL-based controllers adopt a robust strategy that works across penetration rates whereas the feedback controllers degrade immediately upon penetration rate variation. We investigate the feasibility of both action and observation decentralization and demonstrate that effective strategies are possible using purely local sensing. Finally, we open-source our code at https://github.com/eugenevinitsky/decentralized_bottlenecks.

Robust Reinforcement Learning using Adversarial Populations

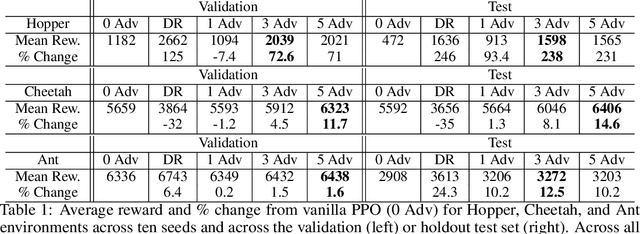
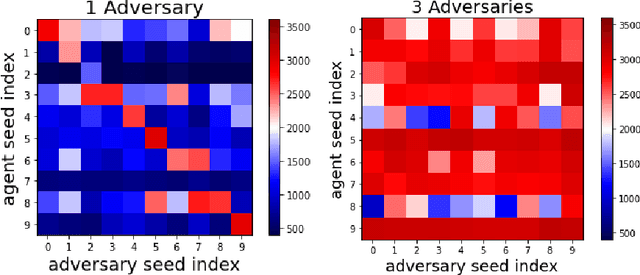
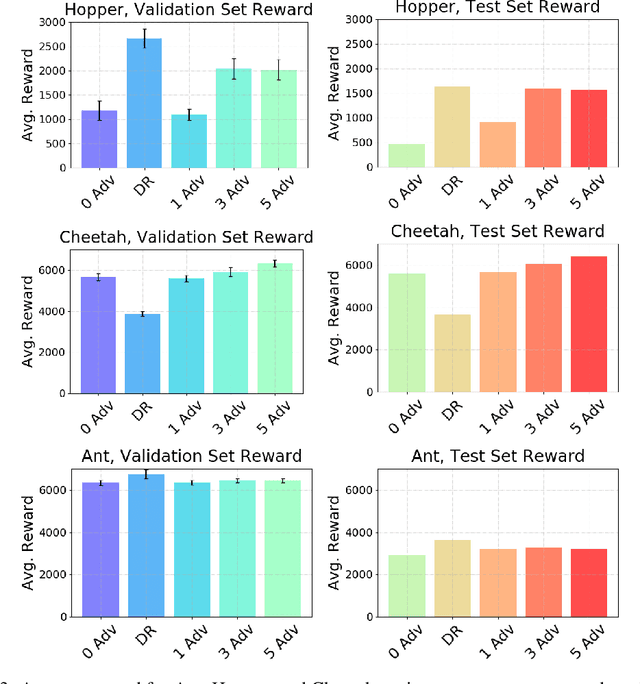
Reinforcement Learning (RL) is an effective tool for controller design but can struggle with issues of robustness, failing catastrophically when the underlying system dynamics are perturbed. The Robust RL formulation tackles this by adding worst-case adversarial noise to the dynamics and constructing the noise distribution as the solution to a zero-sum minimax game. However, existing work on learning solutions to the Robust RL formulation has primarily focused on training a single RL agent against a single adversary. In this work, we demonstrate that using a single adversary does not consistently yield robustness to dynamics variations under standard parametrizations of the adversary; the resulting policy is highly exploitable by new adversaries. We propose a population-based augmentation to the Robust RL formulation in which we randomly initialize a population of adversaries and sample from the population uniformly during training. We empirically validate across robotics benchmarks that the use of an adversarial population results in a more robust policy that also improves out-of-distribution generalization. Finally, we demonstrate that this approach provides comparable robustness and generalization as domain randomization on these benchmarks while avoiding a ubiquitous domain randomization failure mode.

Simulation to Scaled City: Zero-Shot Policy Transfer for Traffic Control via Autonomous Vehicles

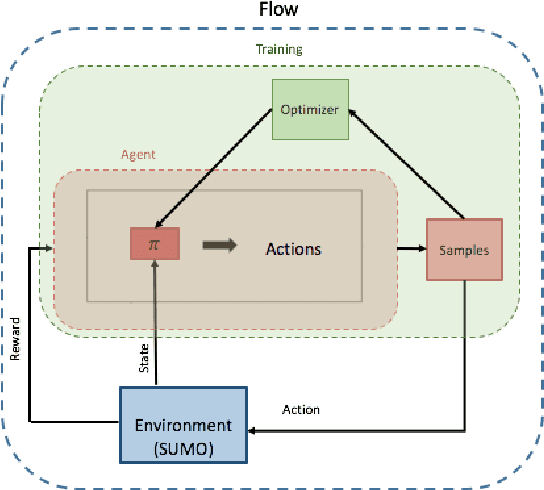
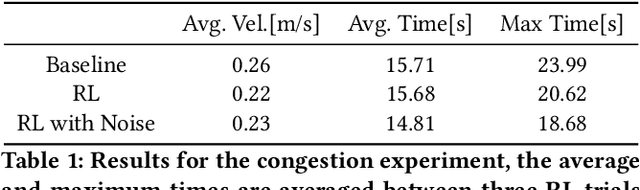
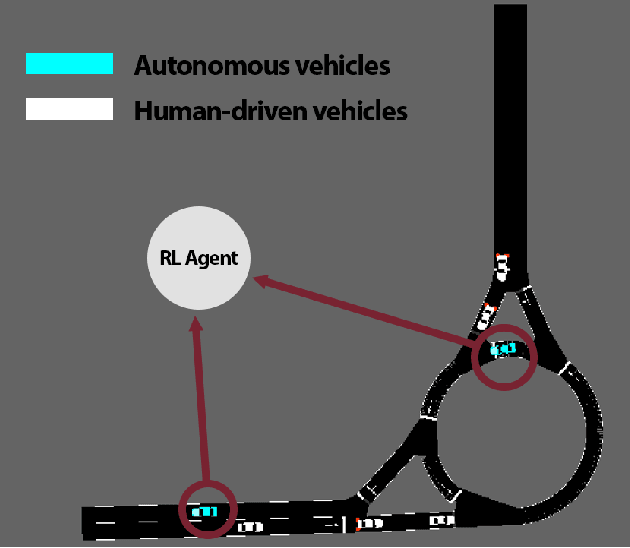
Using deep reinforcement learning, we train control policies for autonomous vehicles leading a platoon of vehicles onto a roundabout. Using Flow, a library for deep reinforcement learning in micro-simulators, we train two policies, one policy with noise injected into the state and action space and one without any injected noise. In simulation, the autonomous vehicle learns an emergent metering behavior for both policies in which it slows to allow for smoother merging. We then directly transfer this policy without any tuning to the University of Delaware Scaled Smart City (UDSSC), a 1:25 scale testbed for connected and automated vehicles. We characterize the performance of both policies on the scaled city. We show that the noise-free policy winds up crashing and only occasionally metering. However, the noise-injected policy consistently performs the metering behavior and remains collision-free, suggesting that the noise helps with the zero-shot policy transfer. Additionally, the transferred, noise-injected policy leads to a 5% reduction of average travel time and a reduction of 22% in maximum travel time in the UDSSC. Videos of the controllers can be found at https://sites.google.com/view/iccps-policy-transfer.

Minimizing Regret on Reflexive Banach Spaces and Learning Nash Equilibria in Continuous Zero-Sum Games

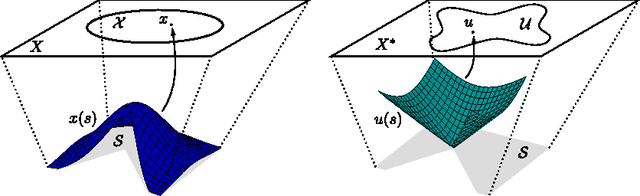
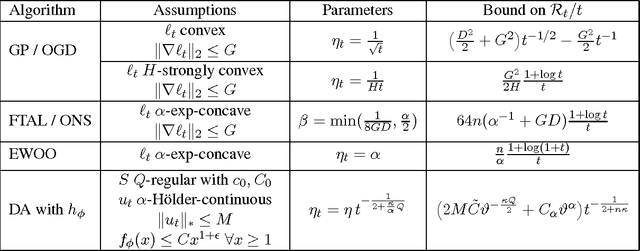
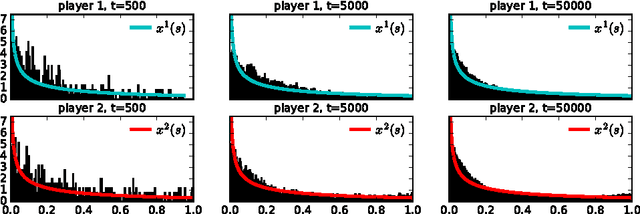
We study a general version of the adversarial online learning problem. We are given a decision set $\mathcal{X}$ in a reflexive Banach space $X$ and a sequence of reward vectors in the dual space of $X$. At each iteration, we choose an action from $\mathcal{X}$, based on the observed sequence of previous rewards. Our goal is to minimize regret, defined as the gap between the realized reward and the reward of the best fixed action in hindsight. Using results from infinite dimensional convex analysis, we generalize the method of Dual Averaging (or Follow the Regularized Leader) to our setting and obtain general upper bounds on the worst-case regret that subsume a wide range of results from the literature. Under the assumption of uniformly continuous rewards, we obtain explicit anytime regret bounds in a setting where the decision set is the set of probability distributions on a compact metric space $S$ whose Radon-Nikodym derivatives are elements of $L^p(S)$ for some $p > 1$. Importantly, we make no convexity assumptions on either the set $S$ or the reward functions. We also prove a general lower bound on the worst-case regret for any online algorithm. We then apply these results to the problem of learning in repeated continuous two-player zero-sum games, in which players' strategy sets are compact metric spaces. In doing so, we first prove that if both players play a Hannan-consistent strategy, then with probability 1 the empirical distributions of play weakly converge to the set of Nash equilibria of the game. We then show that, under mild assumptions, Dual Averaging on the (infinite-dimensional) space of probability distributions indeed achieves Hannan-consistency. Finally, we illustrate our results through numerical examples.

Arriving on time: estimating travel time distributions on large-scale road networks

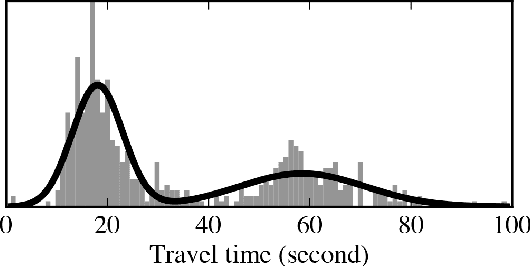
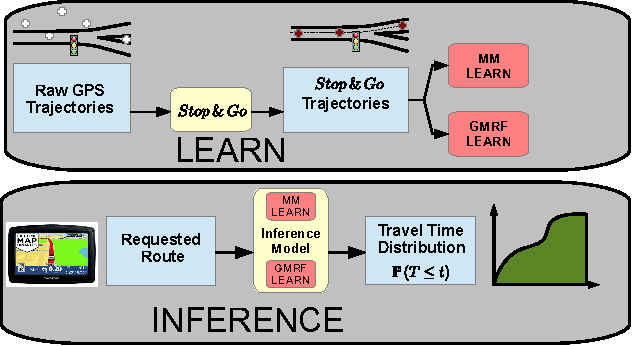
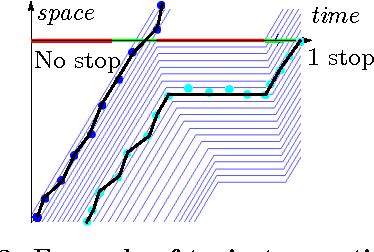
Most optimal routing problems focus on minimizing travel time or distance traveled. Oftentimes, a more useful objective is to maximize the probability of on-time arrival, which requires statistical distributions of travel times, rather than just mean values. We propose a method to estimate travel time distributions on large-scale road networks, using probe vehicle data collected from GPS. We present a framework that works with large input of data, and scales linearly with the size of the network. Leveraging the planar topology of the graph, the method computes efficiently the time correlations between neighboring streets. First, raw probe vehicle traces are compressed into pairs of travel times and number of stops for each traversed road segment using a `stop-and-go' algorithm developed for this work. The compressed data is then used as input for training a path travel time model, which couples a Markov model along with a Gaussian Markov random field. Finally, scalable inference algorithms are developed for obtaining path travel time distributions from the composite MM-GMRF model. We illustrate the accuracy and scalability of our model on a 505,000 road link network spanning the San Francisco Bay Area.

The path inference filter: model-based low-latency map matching of probe vehicle data

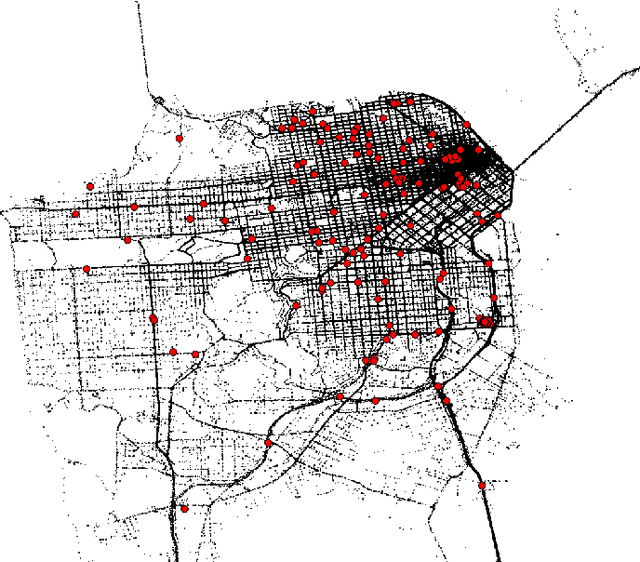
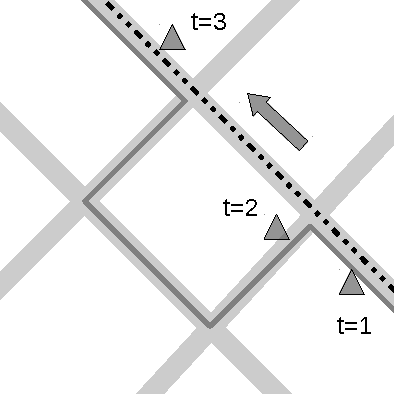
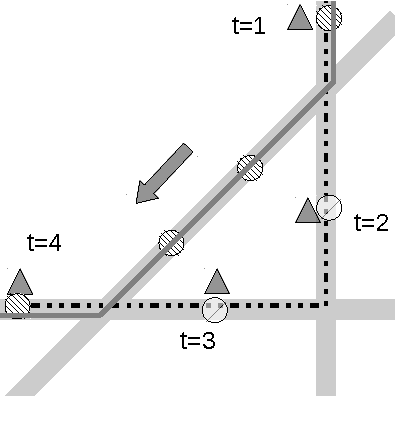
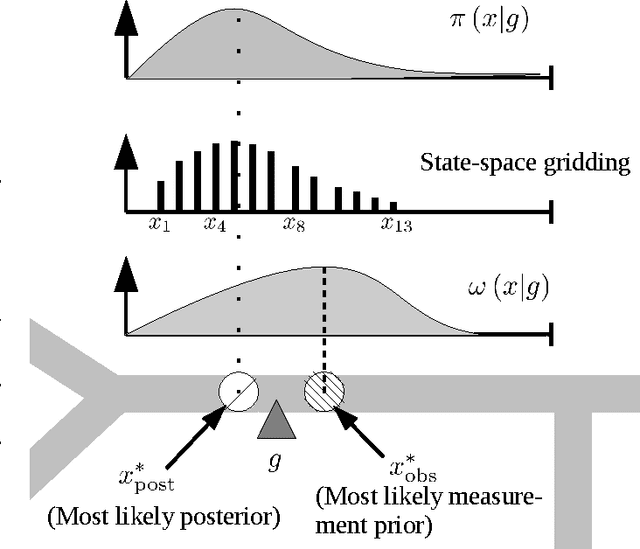
We consider the problem of reconstructing vehicle trajectories from sparse sequences of GPS points, for which the sampling interval is between 10 seconds and 2 minutes. We introduce a new class of algorithms, called altogether path inference filter (PIF), that maps GPS data in real time, for a variety of trade-offs and scenarios, and with a high throughput. Numerous prior approaches in map-matching can be shown to be special cases of the path inference filter presented in this article. We present an efficient procedure for automatically training the filter on new data, with or without ground truth observations. The framework is evaluated on a large San Francisco taxi dataset and is shown to improve upon the current state of the art. This filter also provides insights about driving patterns of drivers. The path inference filter has been deployed at an industrial scale inside the Mobile Millennium traffic information system, and is used to map fleets of data in San Francisco, Sacramento, Stockholm and Porto.