Tradeoffs between Convergence Speed and Reconstruction Accuracy in Inverse Problems

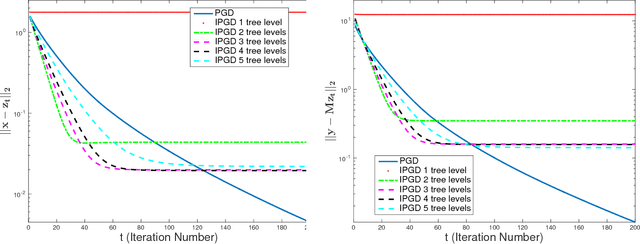
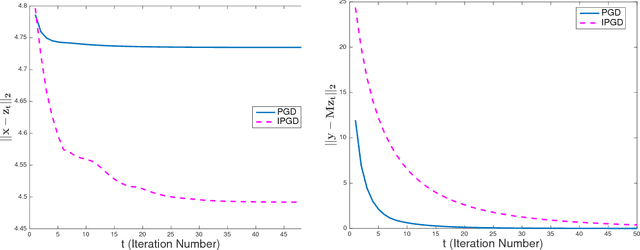
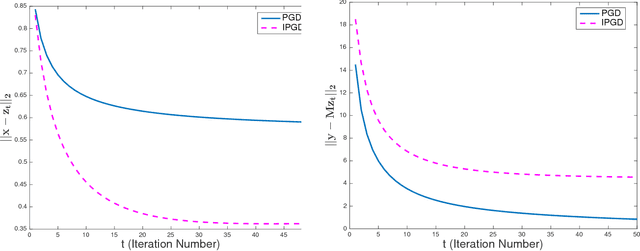
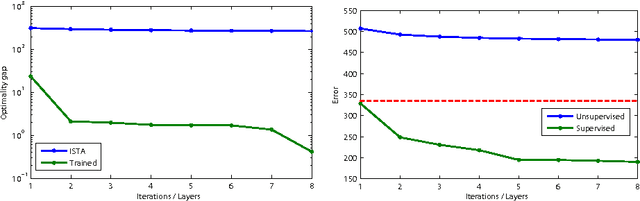
Solving inverse problems with iterative algorithms is popular, especially for large data. Due to time constraints, the number of possible iterations is usually limited, potentially affecting the achievable accuracy. Given an error one is willing to tolerate, an important question is whether it is possible to modify the original iterations to obtain faster convergence to a minimizer achieving the allowed error without increasing the computational cost of each iteration considerably. Relying on recent recovery techniques developed for settings in which the desired signal belongs to some low-dimensional set, we show that using a coarse estimate of this set may lead to faster convergence at the cost of an additional reconstruction error related to the accuracy of the set approximation. Our theory ties to recent advances in sparse recovery, compressed sensing, and deep learning. Particularly, it may provide a possible explanation to the successful approximation of the l1-minimization solution by neural networks with layers representing iterations, as practiced in the learned iterative shrinkage-thresholding algorithm (LISTA).

DeepISP: Learning End-to-End Image Processing Pipeline

We present DeepISP, a full end-to-end deep neural model of the camera image signal processing (ISP) pipeline. Our model learns a mapping from the raw low-light mosaiced image to the final visually compelling image and encompasses low-level tasks such as demosaicing and denoising as well as higher-level tasks such as color correction and image adjustment. The training and evaluation of the pipeline was performed on a dedicated dataset containing pairs of low-light and well-lit images captured by a Samsung S7 smartphone camera in both raw and processed JPEG formats. The proposed solution achieves state-of-the-art performance in objective evaluation of PSNR on the subtask of joint denoising and demosaicing. For the full end-to-end pipeline, it achieves better visual quality compared to the manufacturer ISP, in both a subjective human assessment and when rated by a deep model trained for assessing image quality.

Towards CT-quality Ultrasound Imaging using Deep Learning

The cost-effectiveness and practical harmlessness of ultrasound imaging have made it one of the most widespread tools for medical diagnosis. Unfortunately, the beam-forming based image formation produces granular speckle noise, blurring, shading and other artifacts. To overcome these effects, the ultimate goal would be to reconstruct the tissue acoustic properties by solving a full wave propagation inverse problem. In this work, we make a step towards this goal, using Multi-Resolution Convolutional Neural Networks (CNN). As a result, we are able to reconstruct CT-quality images from the reflected ultrasound radio-frequency(RF) data obtained by simulation from real CT scans of a human body. We also show that CNN is able to imitate existing computationally heavy despeckling methods, thereby saving orders of magnitude in computations and making them amenable to real-time applications.

Deep Functional Maps: Structured Prediction for Dense Shape Correspondence

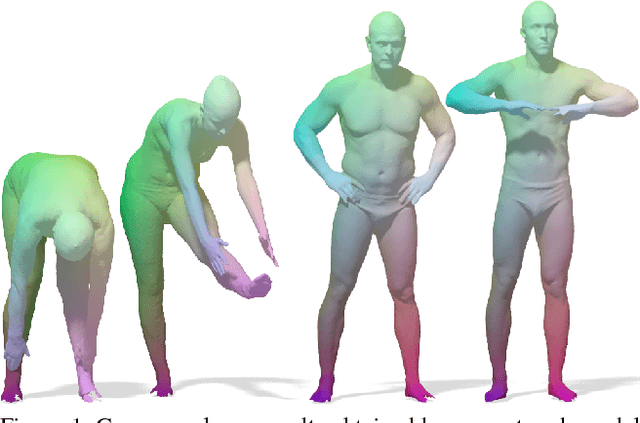
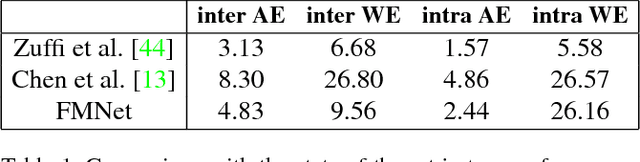
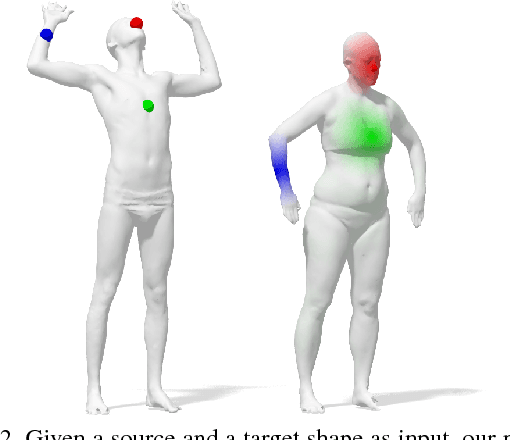
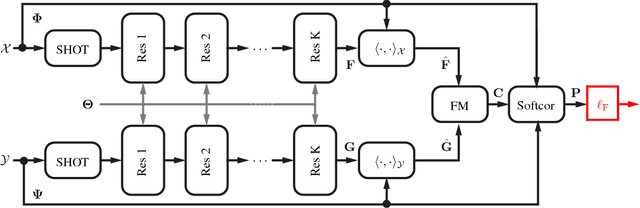
We introduce a new framework for learning dense correspondence between deformable 3D shapes. Existing learning based approaches model shape correspondence as a labelling problem, where each point of a query shape receives a label identifying a point on some reference domain; the correspondence is then constructed a posteriori by composing the label predictions of two input shapes. We propose a paradigm shift and design a structured prediction model in the space of functional maps, linear operators that provide a compact representation of the correspondence. We model the learning process via a deep residual network which takes dense descriptor fields defined on two shapes as input, and outputs a soft map between the two given objects. The resulting correspondence is shown to be accurate on several challenging benchmarks comprising multiple categories, synthetic models, real scans with acquisition artifacts, topological noise, and partiality.

Deep Class Aware Denoising

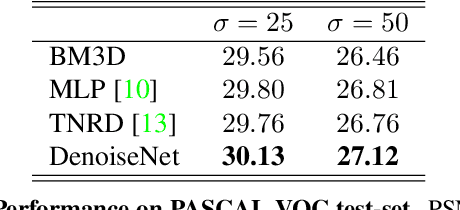
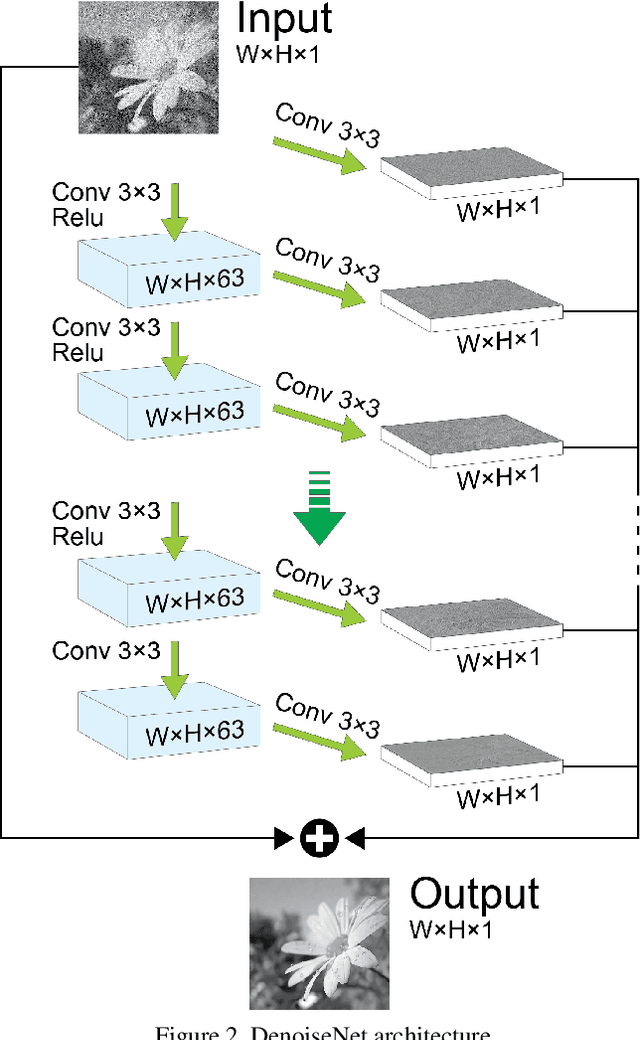
The increasing demand for high image quality in mobile devices brings forth the need for better computational enhancement techniques, and image denoising in particular. At the same time, the images captured by these devices can be categorized into a small set of semantic classes. However simple, this observation has not been exploited in image denoising until now. In this paper, we demonstrate how the reconstruction quality improves when a denoiser is aware of the type of content in the image. To this end, we first propose a new fully convolutional deep neural network architecture which is simple yet powerful as it achieves state-of-the-art performance even without being class-aware. We further show that a significant boost in performance of up to $0.4$ dB PSNR can be achieved by making our network class-aware, namely, by fine-tuning it for images belonging to a specific semantic class. Relying on the hugely successful existing image classifiers, this research advocates for using a class-aware approach in all image enhancement tasks.

Deep Convolutional Denoising of Low-Light Images

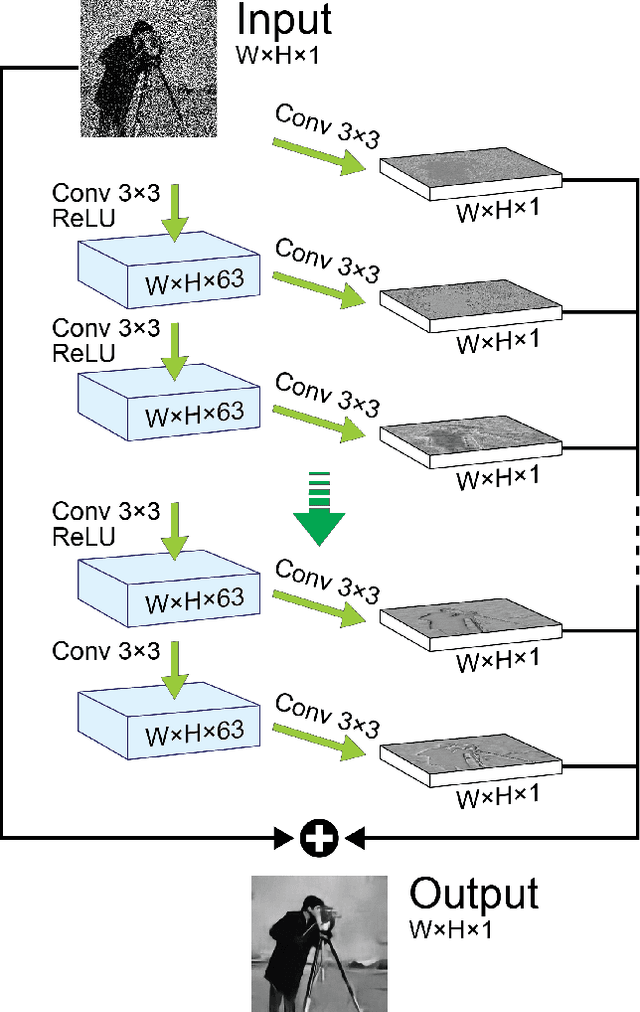
Poisson distribution is used for modeling noise in photon-limited imaging. While canonical examples include relatively exotic types of sensing like spectral imaging or astronomy, the problem is relevant to regular photography now more than ever due to the booming market for mobile cameras. Restricted form factor limits the amount of absorbed light, thus computational post-processing is called for. In this paper, we make use of the powerful framework of deep convolutional neural networks for Poisson denoising. We demonstrate how by training the same network with images having a specific peak value, our denoiser outperforms previous state-of-the-art by a large margin both visually and quantitatively. Being flexible and data-driven, our solution resolves the heavy ad hoc engineering used in previous methods and is an order of magnitude faster. We further show that by adding a reasonable prior on the class of the image being processed, another significant boost in performance is achieved.

Deep Neural Networks with Random Gaussian Weights: A Universal Classification Strategy?

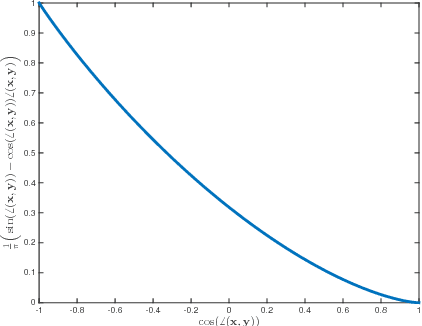
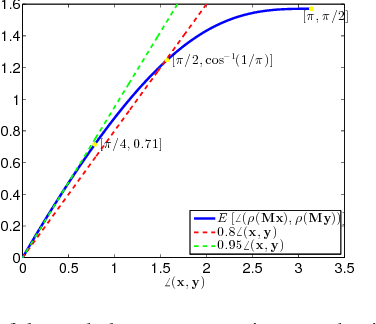
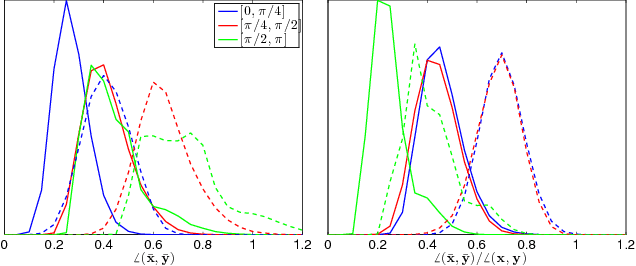
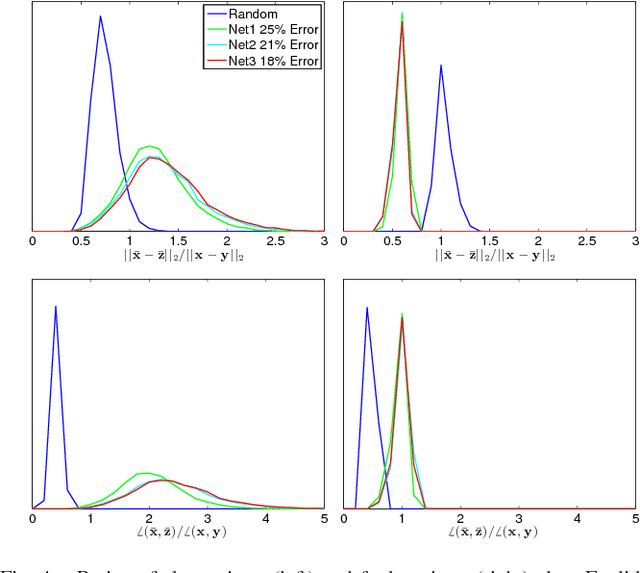
Three important properties of a classification machinery are: (i) the system preserves the core information of the input data; (ii) the training examples convey information about unseen data; and (iii) the system is able to treat differently points from different classes. In this work we show that these fundamental properties are satisfied by the architecture of deep neural networks. We formally prove that these networks with random Gaussian weights perform a distance-preserving embedding of the data, with a special treatment for in-class and out-of-class data. Similar points at the input of the network are likely to have a similar output. The theoretical analysis of deep networks here presented exploits tools used in the compressed sensing and dictionary learning literature, thereby making a formal connection between these important topics. The derived results allow drawing conclusions on the metric learning properties of the network and their relation to its structure, as well as providing bounds on the required size of the training set such that the training examples would represent faithfully the unseen data. The results are validated with state-of-the-art trained networks.

On the Stability of Deep Networks

In this work we study the properties of deep neural networks (DNN) with random weights. We formally prove that these networks perform a distance-preserving embedding of the data. Based on this we then draw conclusions on the size of the training data and the networks' structure. A longer version of this paper with more results and details can be found in (Giryes et al., 2015). In particular, we formally prove in the longer version that DNN with random Gaussian weights perform a distance-preserving embedding of the data, with a special treatment for in-class and out-of-class data.

Sparse similarity-preserving hashing

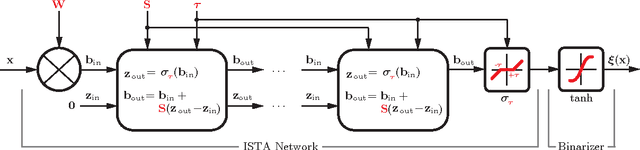
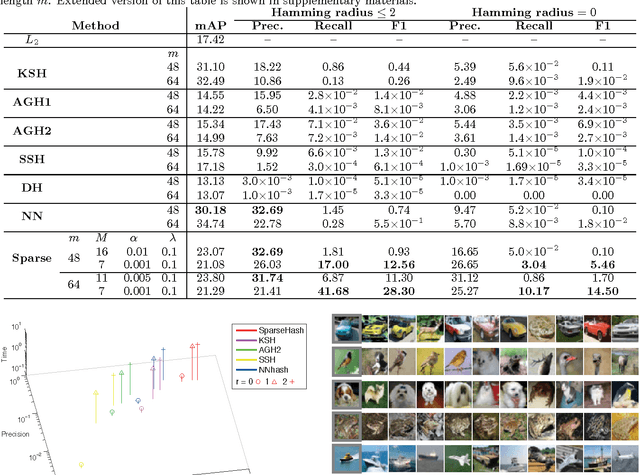
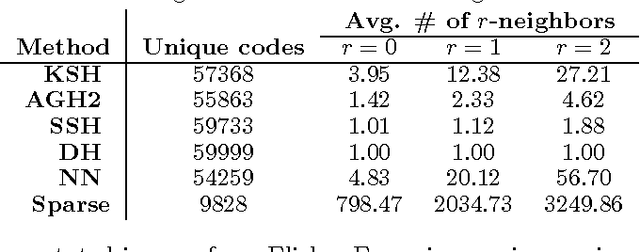
In recent years, a lot of attention has been devoted to efficient nearest neighbor search by means of similarity-preserving hashing. One of the plights of existing hashing techniques is the intrinsic trade-off between performance and computational complexity: while longer hash codes allow for lower false positive rates, it is very difficult to increase the embedding dimensionality without incurring in very high false negatives rates or prohibiting computational costs. In this paper, we propose a way to overcome this limitation by enforcing the hash codes to be sparse. Sparse high-dimensional codes enjoy from the low false positive rates typical of long hashes, while keeping the false negative rates similar to those of a shorter dense hashing scheme with equal number of degrees of freedom. We use a tailored feed-forward neural network for the hashing function. Extensive experimental evaluation involving visual and multi-modal data shows the benefits of the proposed method.

Learning efficient sparse and low rank models

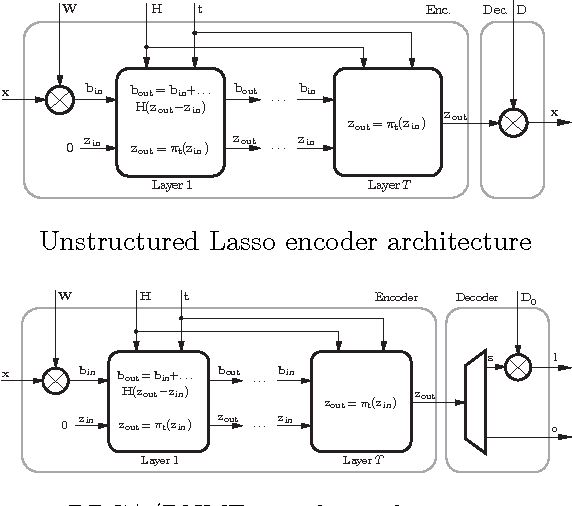
Parsimony, including sparsity and low rank, has been shown to successfully model data in numerous machine learning and signal processing tasks. Traditionally, such modeling approaches rely on an iterative algorithm that minimizes an objective function with parsimony-promoting terms. The inherently sequential structure and data-dependent complexity and latency of iterative optimization constitute a major limitation in many applications requiring real-time performance or involving large-scale data. Another limitation encountered by these modeling techniques is the difficulty of their inclusion in discriminative learning scenarios. In this work, we propose to move the emphasis from the model to the pursuit algorithm, and develop a process-centric view of parsimonious modeling, in which a learned deterministic fixed-complexity pursuit process is used in lieu of iterative optimization. We show a principled way to construct learnable pursuit process architectures for structured sparse and robust low rank models, derived from the iteration of proximal descent algorithms. These architectures learn to approximate the exact parsimonious representation at a fraction of the complexity of the standard optimization methods. We also show that appropriate training regimes allow to naturally extend parsimonious models to discriminative settings. State-of-the-art results are demonstrated on several challenging problems in image and audio processing with several orders of magnitude speedup compared to the exact optimization algorithms.