Noise Estimation Using Density Estimation for Self-Supervised Multimodal Learning

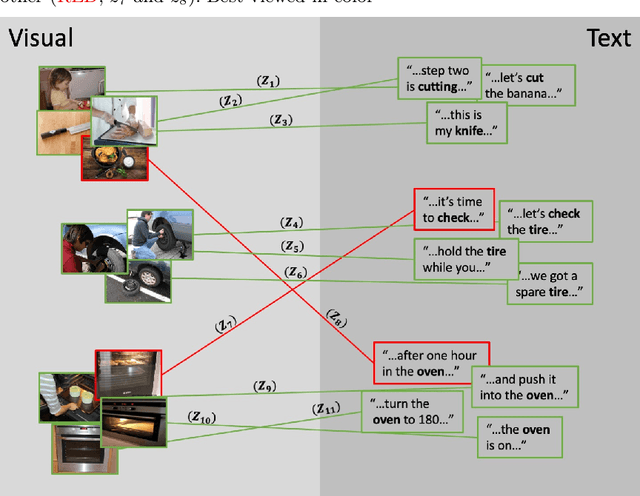
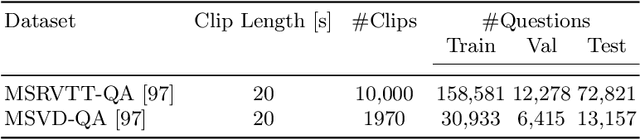
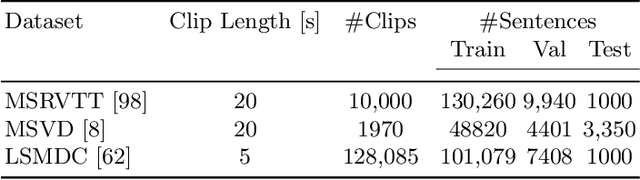
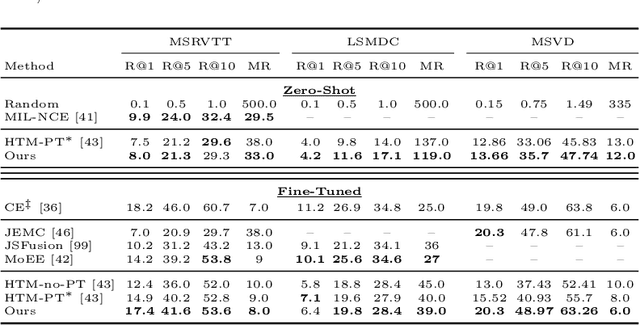
One of the key factors of enabling machine learning models to comprehend and solve real-world tasks is to leverage multimodal data. Unfortunately, annotation of multimodal data is challenging and expensive. Recently, self-supervised multimodal methods that combine vision and language were proposed to learn multimodal representations without annotation. However, these methods choose to ignore the presence of high levels of noise and thus yield sub-optimal results. In this work, we show that the problem of noise estimation for multimodal data can be reduced to a multimodal density estimation task. Using multimodal density estimation, we propose a noise estimation building block for multimodal representation learning that is based strictly on the inherent correlation between different modalities. We demonstrate how our noise estimation can be broadly integrated and achieves comparable results to state-of-the-art performance on five different benchmark datasets for two challenging multimodal tasks: Video Question Answering and Text-To-Video Retrieval.

Robust Quantization: One Model to Rule Them All

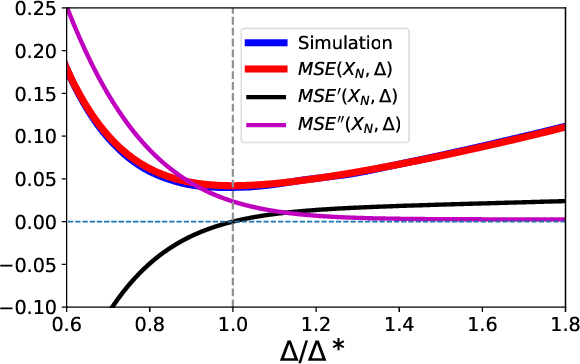
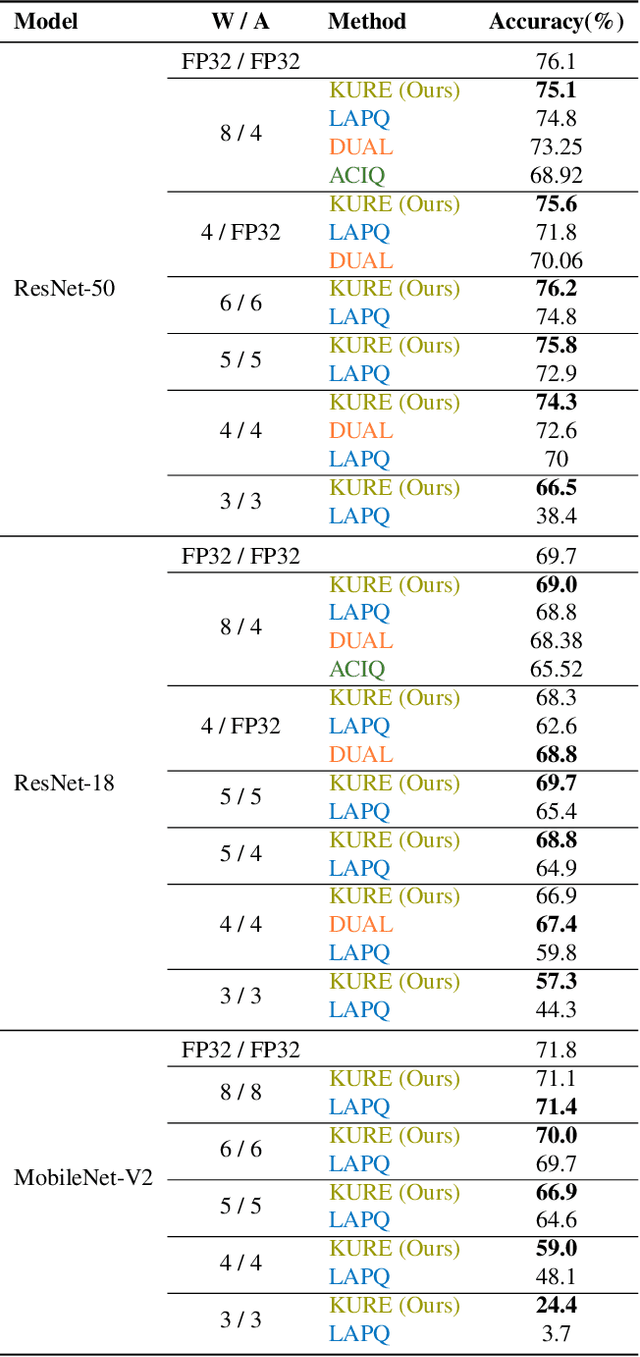
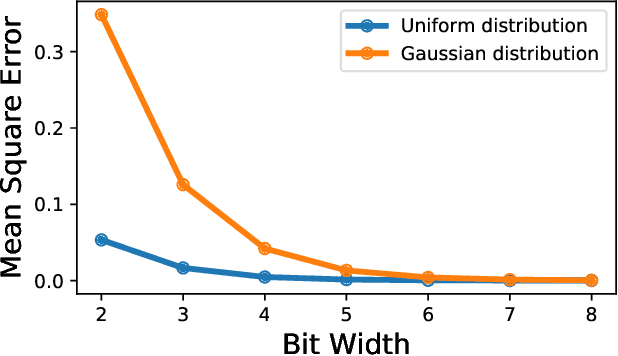
Neural network quantization methods often involve simulating the quantization process during training. This makes the trained model highly dependent on the precise way quantization is performed. Since low-precision accelerators differ in their quantization policies and their supported mix of data-types, a model trained for one accelerator may not be suitable for another. To address this issue, we propose KURE, a method that provides intrinsic robustness to the model against a broad range of quantization implementations. We show that KURE yields a generic model that may be deployed on numerous inference accelerators without a significant loss in accuracy.

MetAdapt: Meta-Learned Task-Adaptive Architecture for Few-Shot Classification

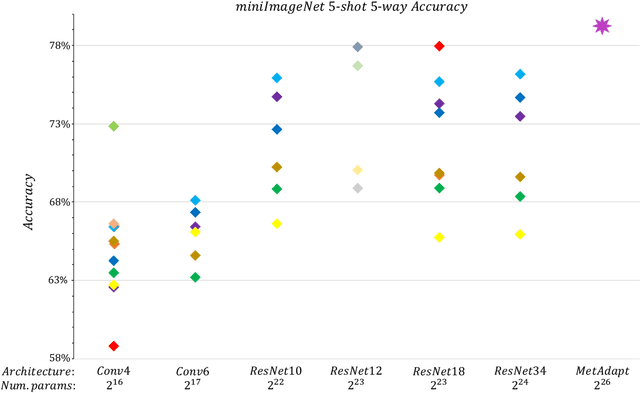
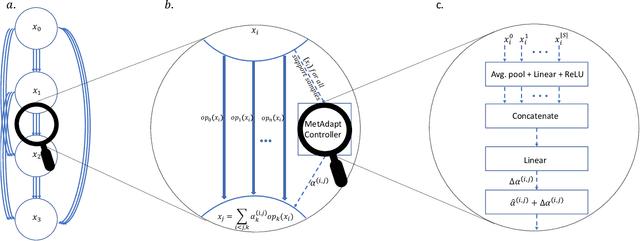
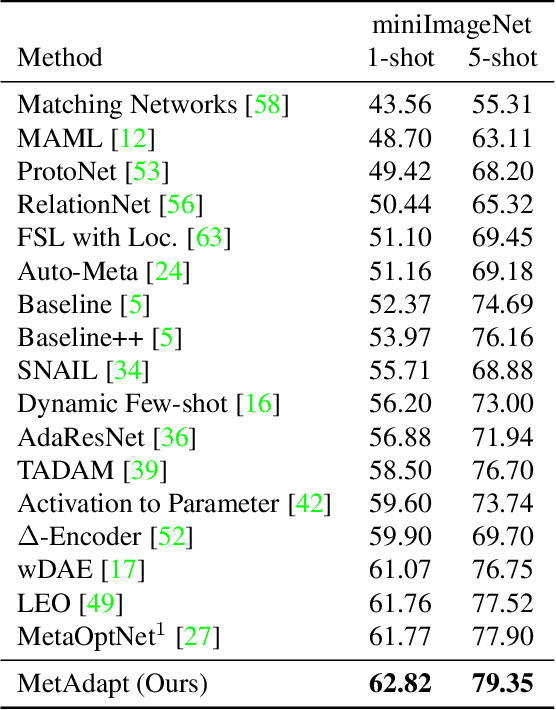
Few-Shot Learning (FSL) is a topic of rapidly growing interest. Typically, in FSL a model is trained on a dataset consisting of many small tasks (meta-tasks) and learns to adapt to novel tasks that it will encounter during test time. This is also referred to as meta-learning. So far, meta-learning FSL methods have focused on optimizing parameters of pre-defined network architectures, in order to make them easily adaptable to novel tasks. Moreover, it was observed that, in general, larger architectures perform better than smaller ones up to a certain saturation point (and even degrade due to over-fitting). However, little attention has been given to explicitly optimizing the architectures for FSL, nor to an adaptation of the architecture at test time to particular novel tasks. In this work, we propose to employ tools borrowed from the Differentiable Neural Architecture Search (D-NAS) literature in order to optimize the architecture for FSL without over-fitting. Additionally, to make the architecture task adaptive, we propose the concept of `MetAdapt Controller' modules. These modules are added to the model and are meta-trained to predict the optimal network connections for a given novel task. Using the proposed approach we observe state-of-the-art results on two popular few-shot benchmarks: miniImageNet and FC100.

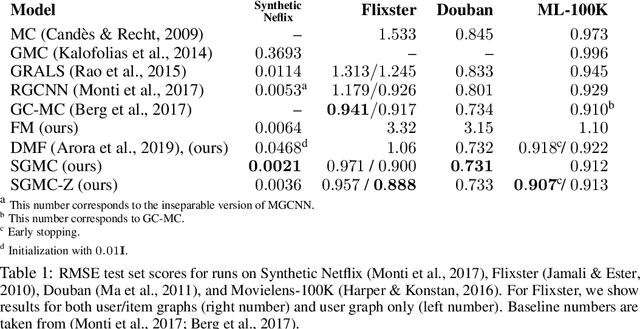
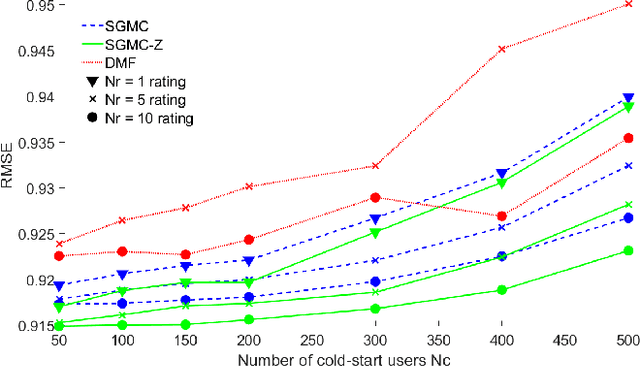
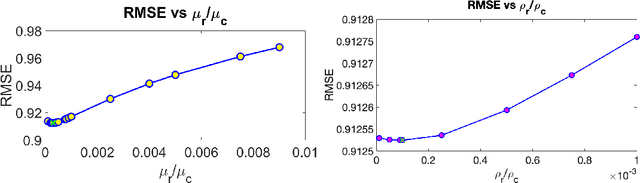
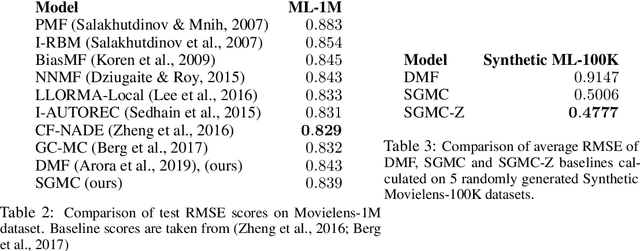
Deep geometric matrix completion: Are we doing it right?

We address the problem of reconstructing a matrix from a subset of its entries. Current methods, branded as geometric matrix completion, augment classical rank regularization techniques by incorporating geometric information into the solution. This information is usually provided as graphs encoding relations between rows/columns. In this work we propose a simple spectral approach for solving the matrix completion problem, via the framework of functional maps. We introduce the zoomout loss, a multiresolution spectral geometric loss inspired by recent advances in shape correspondence, whose minimization leads to state-of-the-art results on various recommender systems datasets. Surprisingly, for some datasets we were able to achieve comparable results even without incorporating geometric information. This puts into question both the quality of such information and current methods' ability to use it in a meaningful and efficient way.

Localization with Limited Annotation for Chest X-rays

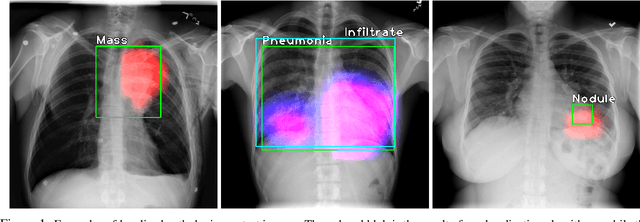
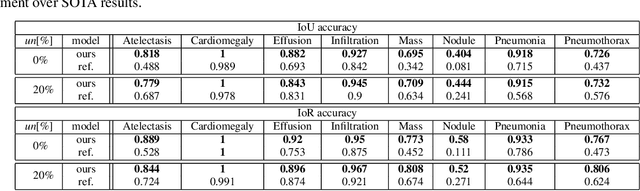
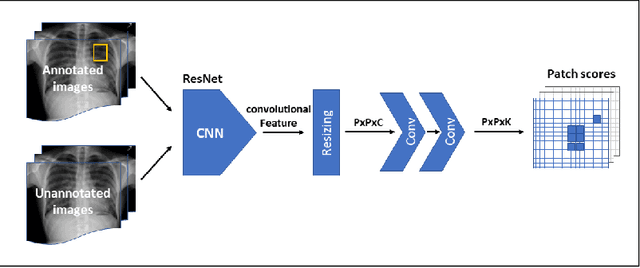
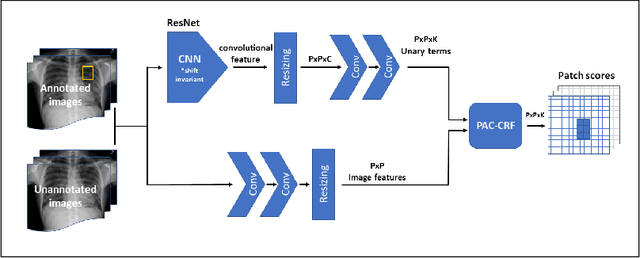
Localization of an object within an image is a common task in medical imaging. Learning to localize or detect objects typically requires the collection of data which has been labelled with bounding boxes or similar annotations, which can be very time consuming and expensive. A technique which could perform such learning with much less annotation would, therefore, be quite valuable. We present such a technique for localization with limited annotation, in which the number of images with bounding boxes can be a small fraction of the total dataset (e.g. less than 1%); all other images only possess a whole image label and no bounding box. We propose a novel loss function for tackling this problem; the loss is a continuous relaxation of a well-defined discrete formulation of weakly supervised learning and is numerically well-posed. Furthermore, we propose a new architecture which accounts for both patch dependence and shift-invariance, through the inclusion of CRF layers and anti-aliasing filters, respectively. We apply our technique to the localization of thoracic diseases in chest X-ray images and demonstrate state-of-the-art localization performance on the ChestX-ray14 dataset.

PILOT: Physics-Informed Learned Optimal Trajectories for Accelerated MRI

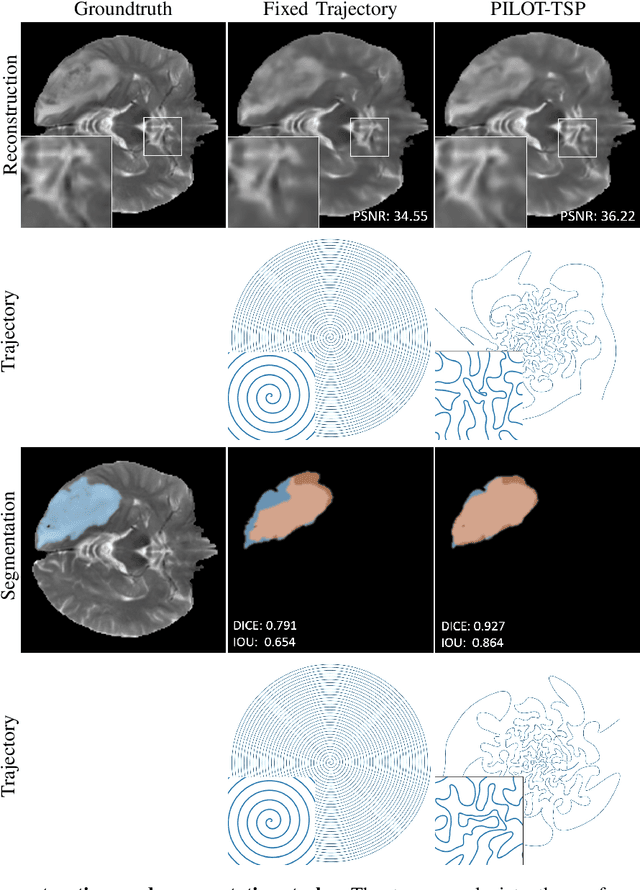
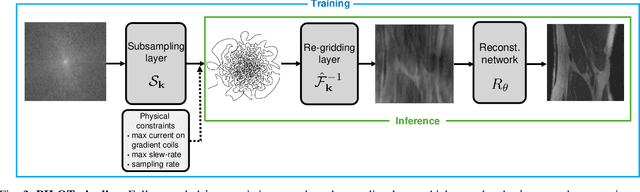
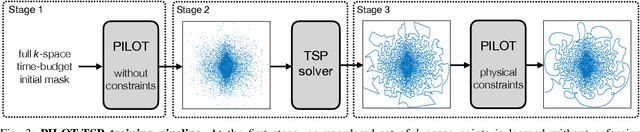
Magnetic Resonance Imaging (MRI) has long been considered to be among "the gold standards" of diagnostic medical imaging. The long acquisition times, however, render MRI prone to motion artifacts, let alone their adverse contribution to the relative high costs of MRI examination. Over the last few decades, multiple studies have focused on the development of both physical and post-processing methods for accelerated acquisition of MRI scans. These two approaches, however, have so far been addressed separately. On the other hand, recent works in optical computational imaging have demonstrated growing success of concurrent learning-based design of data acquisition and image reconstruction schemes. In this work, we propose a novel approach to the learning of optimal schemes for conjoint acquisition and reconstruction of MRI scans, with the optimization carried out simultaneously with respect to the time-efficiency of data acquisition and the quality of resulting reconstructions. To be of a practical value, the schemes are encoded in the form of general k-space trajectories, whose associated magnetic gradients are constrained to obey a set of predefined hardware requirements (as defined in terms of, e.g., peak currents and maximum slew rates of magnetic gradients). With this proviso in mind, we propose a novel algorithm for the end-to-end training of a combined acquisition-reconstruction pipeline using a deep neural network with differentiable forward- and back-propagation operators. We also demonstrate the effectiveness of the proposed solution in application to both image reconstruction and image segmentation, reporting substantial improvements in terms of acceleration factors as well as the quality of these end tasks.

Horizontal Flows and Manifold Stochastics in Geometric Deep Learning

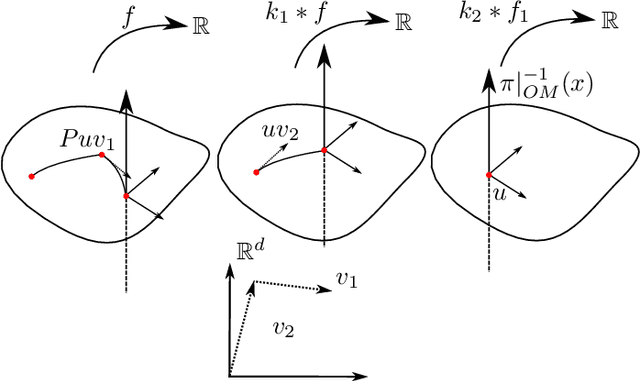
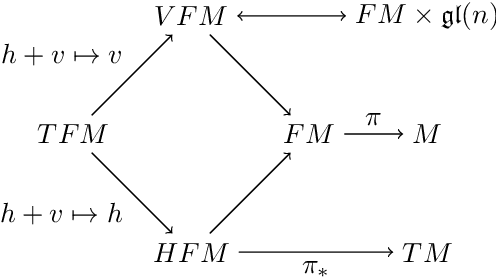
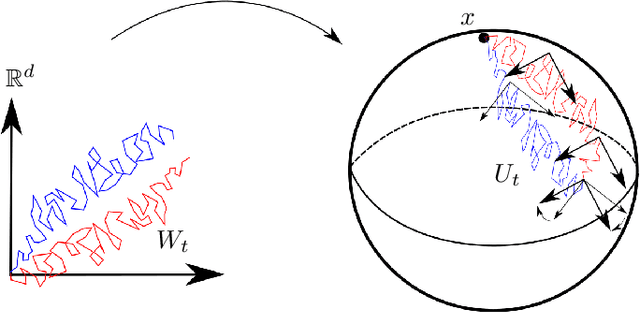
We introduce two constructions in geometric deep learning for 1) transporting orientation-dependent convolutional filters over a manifold in a continuous way and thereby defining a convolution operator that naturally incorporates the rotational effect of holonomy; and 2) allowing efficient evaluation of manifold convolution layers by sampling manifold valued random variables that center around a weighted Brownian motion maximum likelihood mean. Both methods are inspired by stochastics on manifolds and geometric statistics, and provide examples of how stochastic methods -- here horizontal frame bundle flows and non-linear bridge sampling schemes, can be used in geometric deep learning. We outline the theoretical foundation of the two methods, discuss their relation to Euclidean deep networks and existing methodology in geometric deep learning, and establish important properties of the proposed constructions.

Intrinsic Multi-scale Evaluation of Generative Models

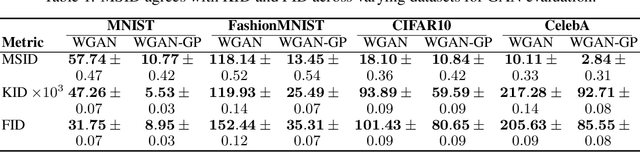
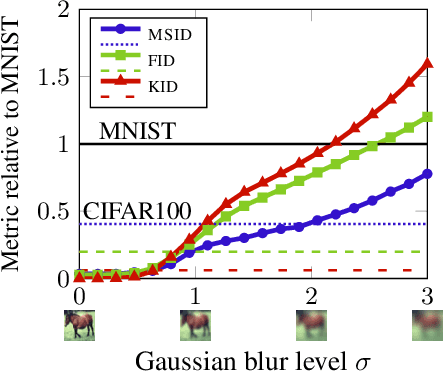
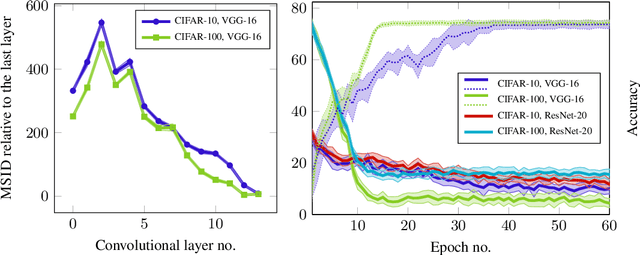
Generative models are often used to sample high-dimensional data points from a manifold with small intrinsic dimension. Existing techniques for comparing generative models focus on global data properties such as mean and covariance; in that sense, they are extrinsic and uni-scale. We develop the first, to our knowledge, intrinsic and multi-scale method for characterizing and comparing underlying data manifolds, based on comparing all data moments by lower-bounding the spectral notion of the Gromov-Wasserstein distance between manifolds. In a thorough experimental study, we demonstrate that our method effectively evaluates the quality of generative models; further, we showcase its efficacy in discerning the disentanglement process in neural networks.

Toward Self-Supervised Object Detection in Unlabeled Videos

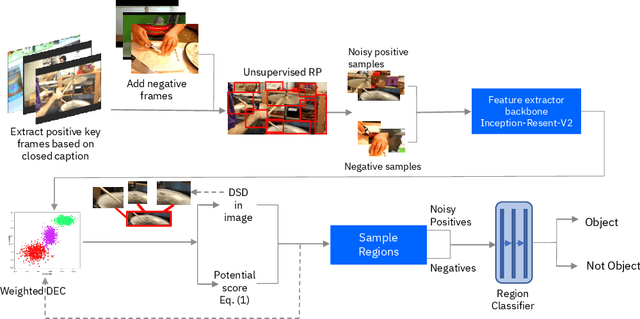
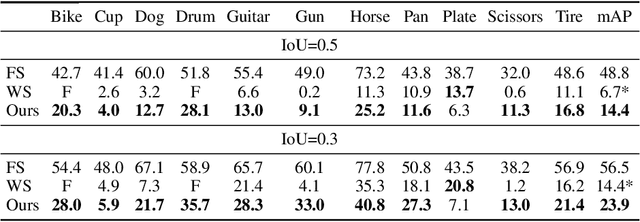
Unlabeled video in the wild presents a valuable, yet so far unharnessed, source of information for learning vision tasks. We present the first attempt of fully self-supervised learning of object detection from subtitled videos without any manual object annotation. To this end, we use the How2 multi-modal collection of instructional videos with English subtitles. We pose the problem as learning with a weakly- and noisily-labeled data, and propose a novel training model that can confront high noise levels, and yet train a classifier to localize the object of interest in the video frames, without any manual labeling involved. We evaluate our approach on a set of 11 manually annotated objects in over 5000 frames and compare it to an existing weakly-supervised approach as baseline. Benchmark data and code will be released upon acceptance of the paper.

Self-supervised learning of inverse problem solvers in medical imaging

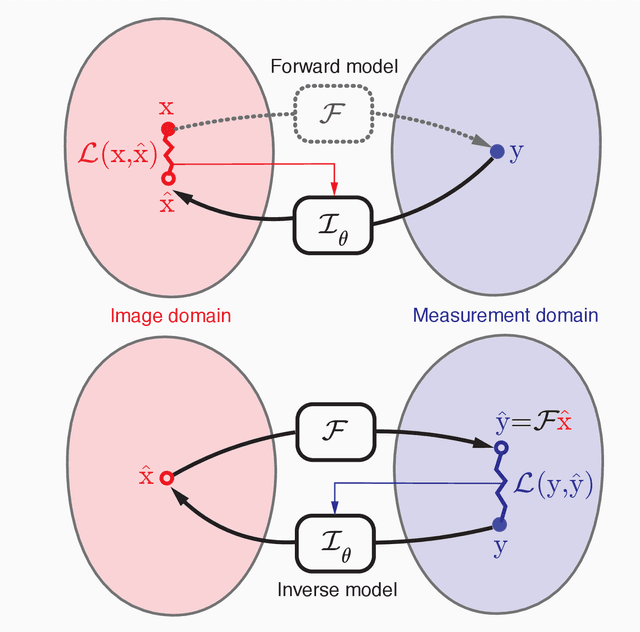
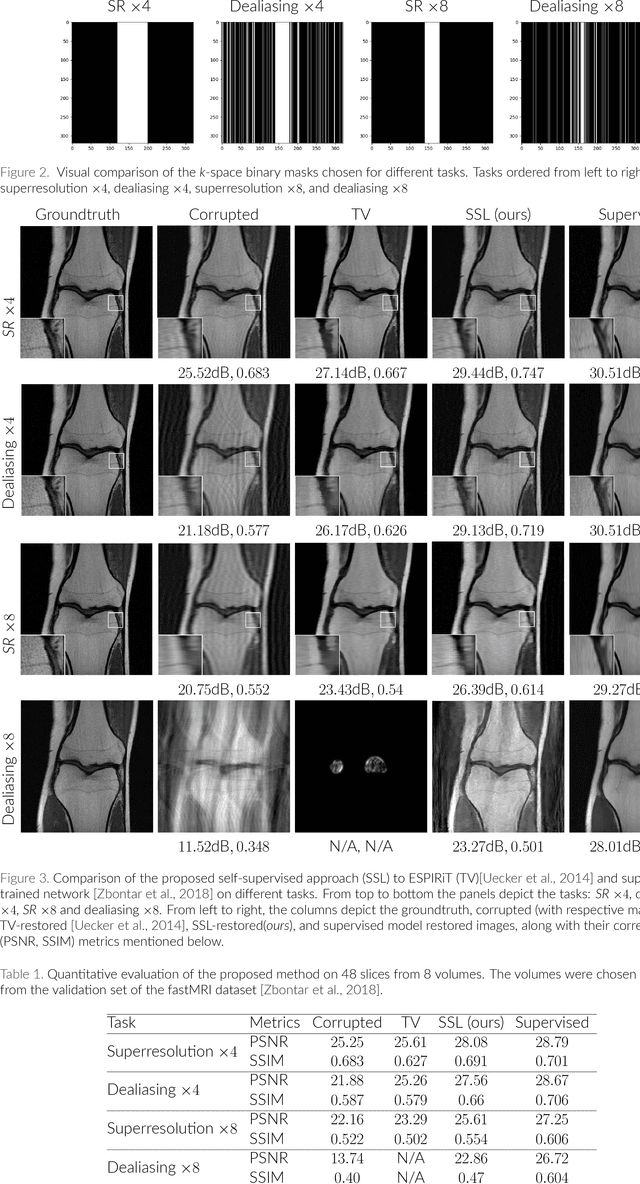
In the past few years, deep learning-based methods have demonstrated enormous success for solving inverse problems in medical imaging. In this work, we address the following question:\textit{Given a set of measurements obtained from real imaging experiments, what is the best way to use a learnable model and the physics of the modality to solve the inverse problem and reconstruct the latent image?} Standard supervised learning based methods approach this problem by collecting data sets of known latent images and their corresponding measurements. However, these methods are often impractical due to the lack of availability of appropriately sized training sets, and, more generally, due to the inherent difficulty in measuring the "groundtruth" latent image. In light of this, we propose a self-supervised approach to training inverse models in medical imaging in the absence of aligned data. Our method only requiring access to the measurements and the forward model at training. We showcase its effectiveness on inverse problems arising in accelerated magnetic resonance imaging (MRI).