Savage-Dickey density ratio estimation with normalizing flows for Bayesian model comparison

A core motivation of science is to evaluate which scientific model best explains observed data. Bayesian model comparison provides a principled statistical approach to comparing scientific models and has found widespread application within cosmology and astrophysics. Calculating the Bayesian evidence is computationally challenging, especially as we continue to explore increasingly more complex models. The Savage-Dickey density ratio (SDDR) provides a method to calculate the Bayes factor (evidence ratio) between two nested models using only posterior samples from the super model. The SDDR requires the calculation of a normalised marginal distribution over the extra parameters of the super model, which has typically been performed using classical density estimators, such as histograms. Classical density estimators, however, can struggle to scale to high-dimensional settings. We introduce a neural SDDR approach using normalizing flows that can scale to settings where the super model contains a large number of extra parameters. We demonstrate the effectiveness of this neural SDDR methodology applied to both toy and realistic cosmological examples. For a field-level inference setting, we show that Bayes factors computed for a Bayesian hierarchical model (BHM) and simulation-based inference (SBI) approach are consistent, providing further validation that SBI extracts as much cosmological information from the field as the BHM approach. The SDDR estimator with normalizing flows is implemented in the open-source harmonic Python package.

Transfer learning for multifidelity simulation-based inference in cosmology

Simulation-based inference (SBI) enables cosmological parameter estimation when closed-form likelihoods or models are unavailable. However, SBI relies on machine learning for neural compression and density estimation. This requires large training datasets which are prohibitively expensive for high-quality simulations. We overcome this limitation with multifidelity transfer learning, combining less expensive, lower-fidelity simulations with a limited number of high-fidelity simulations. We demonstrate our methodology on dark matter density maps from two separate simulation suites in the hydrodynamical CAMELS Multifield Dataset. Pre-training on dark-matter-only $N$-body simulations reduces the required number of high-fidelity hydrodynamical simulations by a factor between $8$ and $15$, depending on the model complexity, posterior dimensionality, and performance metrics used. By leveraging cheaper simulations, our approach enables performant and accurate inference on high-fidelity models while substantially reducing computational costs.

The future of cosmological likelihood-based inference: accelerated high-dimensional parameter estimation and model comparison

We advocate for a new paradigm of cosmological likelihood-based inference, leveraging recent developments in machine learning and its underlying technology, to accelerate Bayesian inference in high-dimensional settings. Specifically, we combine (i) emulation, where a machine learning model is trained to mimic cosmological observables, e.g. CosmoPower-JAX; (ii) differentiable and probabilistic programming, e.g. JAX and NumPyro, respectively; (iii) scalable Markov chain Monte Carlo (MCMC) sampling techniques that exploit gradients, e.g. Hamiltonian Monte Carlo; and (iv) decoupled and scalable Bayesian model selection techniques that compute the Bayesian evidence purely from posterior samples, e.g. the learned harmonic mean implemented in harmonic. This paradigm allows us to carry out a complete Bayesian analysis, including both parameter estimation and model selection, in a fraction of the time of traditional approaches. First, we demonstrate the application of this paradigm on a simulated cosmic shear analysis for a Stage IV survey in 37- and 39-dimensional parameter spaces, comparing $\Lambda$CDM and a dynamical dark energy model ($w_0w_a$CDM). We recover posterior contours and evidence estimates that are in excellent agreement with those computed by the traditional nested sampling approach while reducing the computational cost from 8 months on 48 CPU cores to 2 days on 12 GPUs. Second, we consider a joint analysis between three simulated next-generation surveys, each performing a 3x2pt analysis, resulting in 157- and 159-dimensional parameter spaces. Standard nested sampling techniques are simply not feasible in this high-dimensional setting, requiring a projected 12 years of compute time on 48 CPU cores; on the other hand, the proposed approach only requires 8 days of compute time on 24 GPUs. All packages used in our analyses are publicly available.

Learned harmonic mean estimation of the marginal likelihood with normalizing flows

Computing the marginal likelihood (also called the Bayesian model evidence) is an important task in Bayesian model selection, providing a principled quantitative way to compare models. The learned harmonic mean estimator solves the exploding variance problem of the original harmonic mean estimation of the marginal likelihood. The learned harmonic mean estimator learns an importance sampling target distribution that approximates the optimal distribution. While the approximation need not be highly accurate, it is critical that the probability mass of the learned distribution is contained within the posterior in order to avoid the exploding variance problem. In previous work a bespoke optimization problem is introduced when training models in order to ensure this property is satisfied. In the current article we introduce the use of normalizing flows to represent the importance sampling target distribution. A flow-based model is trained on samples from the posterior by maximum likelihood estimation. Then, the probability density of the flow is concentrated by lowering the variance of the base distribution, i.e. by lowering its "temperature", ensuring its probability mass is contained within the posterior. This approach avoids the need for a bespoke optimisation problem and careful fine tuning of parameters, resulting in a more robust method. Moreover, the use of normalizing flows has the potential to scale to high dimensional settings. We present preliminary experiments demonstrating the effectiveness of the use of flows for the learned harmonic mean estimator. The harmonic code implementing the learned harmonic mean, which is publicly available, has been updated to now support normalizing flows.

Towards fast machine-learning-assisted Bayesian posterior inference of realistic microseismic events

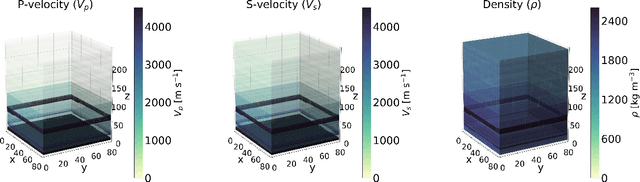
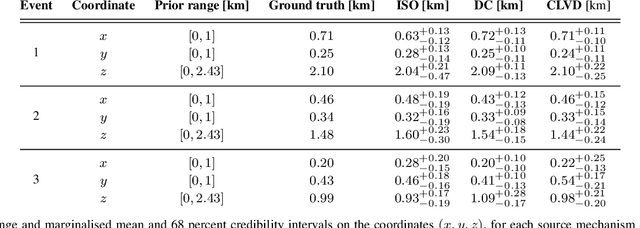
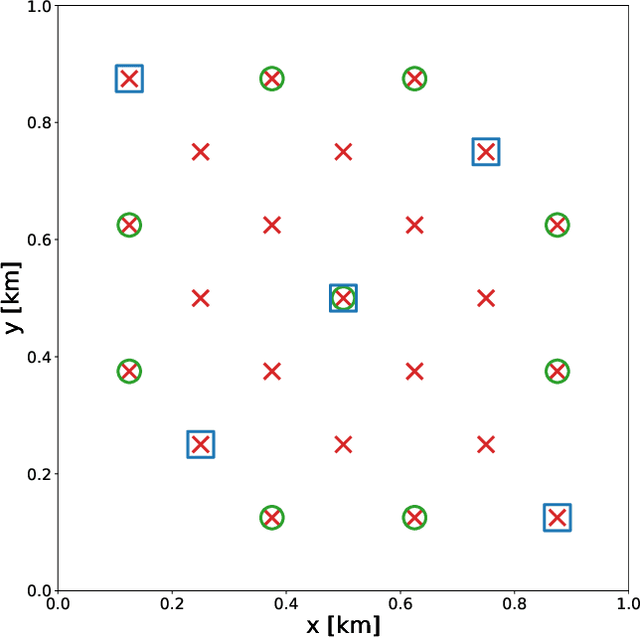
Bayesian inference applied to microseismic activity monitoring allows for principled estimation of the coordinates of microseismic events from recorded seismograms, and their associated uncertainties. However, forward modelling of these microseismic events, necessary to perform Bayesian source inversion, can be prohibitively expensive in terms of computational resources. A viable solution is to train a surrogate model based on machine learning techniques, to emulate the forward model and thus accelerate Bayesian inference. In this paper, we improve on previous work, which considered only sources with isotropic moment tensor. We train a machine learning algorithm on the power spectrum of the recorded pressure wave and show that the trained emulator allows for the complete and fast retrieval of the event coordinates for $\textit{any}$ source mechanism. Moreover, we show that our approach is computationally inexpensive, as it can be run in less than 1 hour on a commercial laptop, while yielding accurate results using less than $10^4$ training seismograms. We additionally demonstrate how the trained emulators can be used to identify the source mechanism through the estimation of the Bayesian evidence. This work lays the foundations for the efficient localisation and characterisation of any recorded seismogram, thus helping to quantify human impact on seismic activity and mitigate seismic hazard.