Akshay Agrawal
Joint Graph Learning and Model Fitting in Laplacian Regularized Stratified Models
May 04, 2023



Abstract:Laplacian regularized stratified models (LRSM) are models that utilize the explicit or implicit network structure of the sub-problems as defined by the categorical features called strata (e.g., age, region, time, forecast horizon, etc.), and draw upon data from neighboring strata to enhance the parameter learning of each sub-problem. They have been widely applied in machine learning and signal processing problems, including but not limited to time series forecasting, representation learning, graph clustering, max-margin classification, and general few-shot learning. Nevertheless, existing works on LRSM have either assumed a known graph or are restricted to specific applications. In this paper, we start by showing the importance and sensitivity of graph weights in LRSM, and provably show that the sensitivity can be arbitrarily large when the parameter scales and sample sizes are heavily imbalanced across nodes. We then propose a generic approach to jointly learn the graph while fitting the model parameters by solving a single optimization problem. We interpret the proposed formulation from both a graph connectivity viewpoint and an end-to-end Bayesian perspective, and propose an efficient algorithm to solve the problem. Convergence guarantees of the proposed optimization algorithm is also provided despite the lack of global strongly smoothness of the Laplacian regularization term typically required in the existing literature, which may be of independent interest. Finally, we illustrate the efficiency of our approach compared to existing methods by various real-world numerical examples.
Minimum-Distortion Embedding
Mar 20, 2021Abstract:We consider the vector embedding problem. We are given a finite set of items, with the goal of assigning a representative vector to each one, possibly under some constraints (such as the collection of vectors being standardized, i.e., have zero mean and unit covariance). We are given data indicating that some pairs of items are similar, and optionally, some other pairs are dissimilar. For pairs of similar items, we want the corresponding vectors to be near each other, and for dissimilar pairs, we want the corresponding vectors to not be near each other, measured in Euclidean distance. We formalize this by introducing distortion functions, defined for some pairs of the items. Our goal is to choose an embedding that minimizes the total distortion, subject to the constraints. We call this the minimum-distortion embedding (MDE) problem. The MDE framework is simple but general. It includes a wide variety of embedding methods, such as spectral embedding, principal component analysis, multidimensional scaling, dimensionality reduction methods (like Isomap and UMAP), force-directed layout, and others. It also includes new embeddings, and provides principled ways of validating historical and new embeddings alike. We develop a projected quasi-Newton method that approximately solves MDE problems and scales to large data sets. We implement this method in PyMDE, an open-source Python package. In PyMDE, users can select from a library of distortion functions and constraints or specify custom ones, making it easy to rapidly experiment with different embeddings. Our software scales to data sets with millions of items and tens of millions of distortion functions. To demonstrate our method, we compute embeddings for several real-world data sets, including images, an academic co-author network, US county demographic data, and single-cell mRNA transcriptomes.
Learning Convex Optimization Models
Jun 18, 2020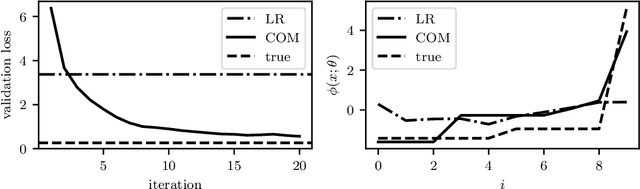
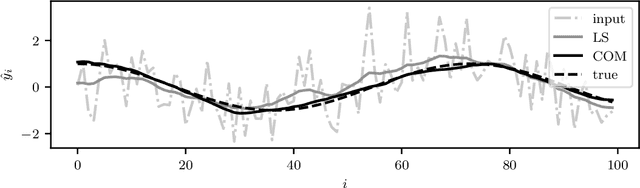

Abstract:A convex optimization model predicts an output from an input by solving a convex optimization problem. The class of convex optimization models is large, and includes as special cases many well-known models like linear and logistic regression. We propose a heuristic for learning the parameters in a convex optimization model given a dataset of input-output pairs, using recently developed methods for differentiating the solution of a convex optimization problem with respect to its parameters. We describe three general classes of convex optimization models, maximum a posteriori (MAP) models, utility maximization models, and agent models, and present a numerical experiment for each.
Learning Convex Optimization Control Policies
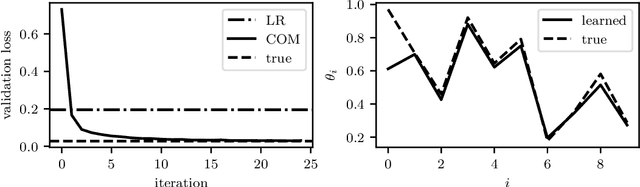
Dec 19, 2019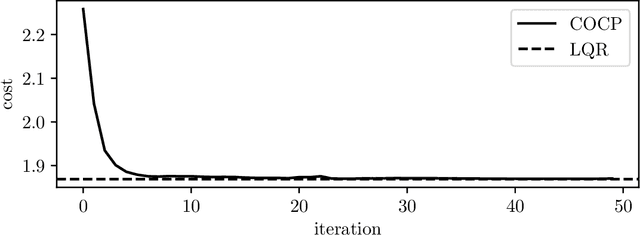
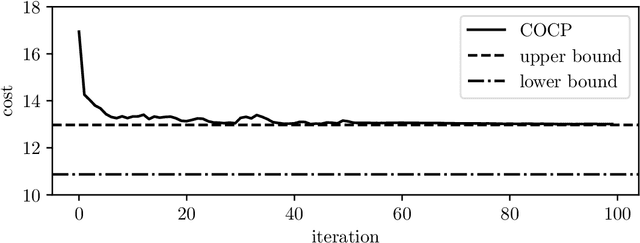
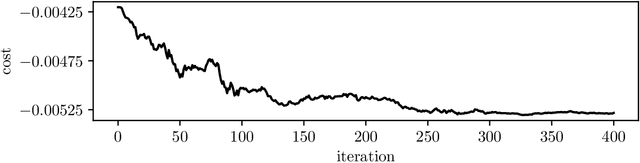
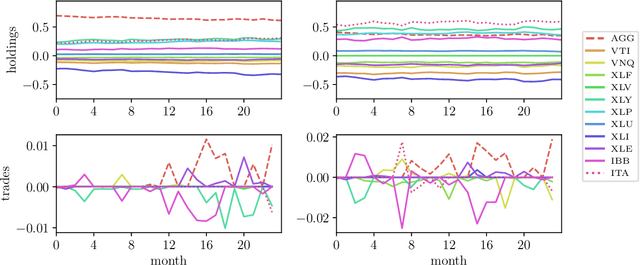
Abstract:Many control policies used in various applications determine the input or action by solving a convex optimization problem that depends on the current state and some parameters. Common examples of such convex optimization control policies (COCPs) include the linear quadratic regulator (LQR), convex model predictive control (MPC), and convex control-Lyapunov or approximate dynamic programming (ADP) policies. These types of control policies are tuned by varying the parameters in the optimization problem, such as the LQR weights, to obtain good performance, judged by application-specific metrics. Tuning is often done by hand, or by simple methods such as a crude grid search. In this paper we propose a method to automate this process, by adjusting the parameters using an approximate gradient of the performance metric with respect to the parameters. Our method relies on recently developed methods that can efficiently evaluate the derivative of the solution of a convex optimization problem with respect to its parameters. We illustrate our method on several examples.
Differentiable Convex Optimization Layers
Oct 28, 2019

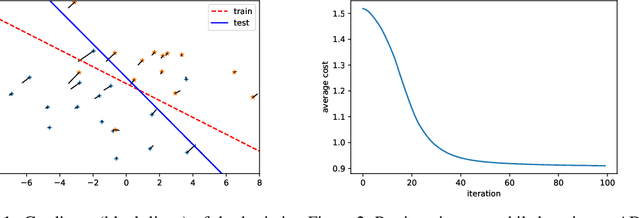
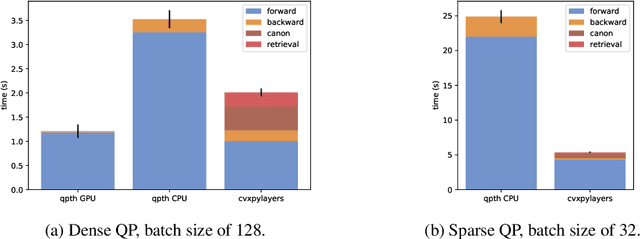
Abstract:Recent work has shown how to embed differentiable optimization problems (that is, problems whose solutions can be backpropagated through) as layers within deep learning architectures. This method provides a useful inductive bias for certain problems, but existing software for differentiable optimization layers is rigid and difficult to apply to new settings. In this paper, we propose an approach to differentiating through disciplined convex programs, a subclass of convex optimization problems used by domain-specific languages (DSLs) for convex optimization. We introduce disciplined parametrized programming, a subset of disciplined convex programming, and we show that every disciplined parametrized program can be represented as the composition of an affine map from parameters to problem data, a solver, and an affine map from the solver's solution to a solution of the original problem (a new form we refer to as affine-solver-affine form). We then demonstrate how to efficiently differentiate through each of these components, allowing for end-to-end analytical differentiation through the entire convex program. We implement our methodology in version 1.1 of CVXPY, a popular Python-embedded DSL for convex optimization, and additionally implement differentiable layers for disciplined convex programs in PyTorch and TensorFlow 2.0. Our implementation significantly lowers the barrier to using convex optimization problems in differentiable programs. We present applications in linear machine learning models and in stochastic control, and we show that our layer is competitive (in execution time) compared to specialized differentiable solvers from past work.
TensorFlow Eager: A Multi-Stage, Python-Embedded DSL for Machine Learning
Feb 27, 2019

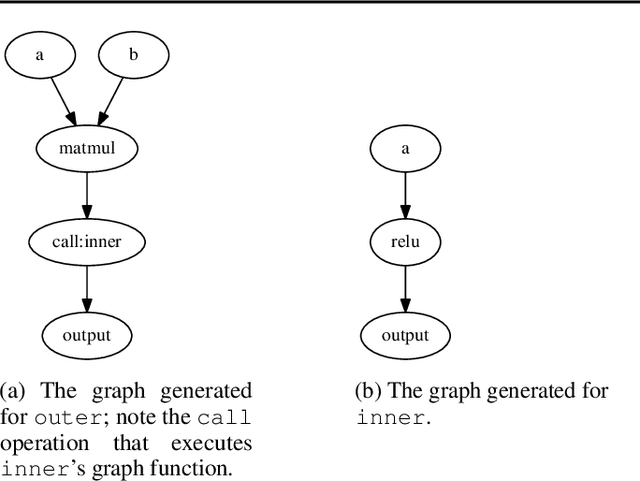
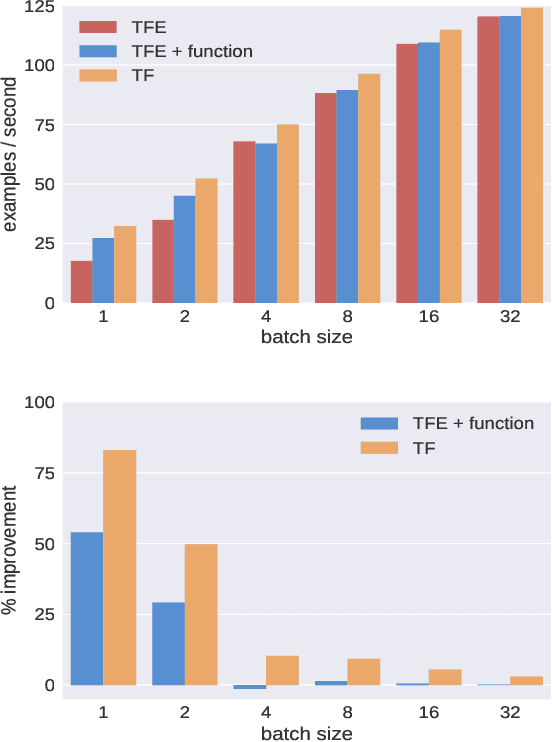
Abstract:TensorFlow Eager is a multi-stage, Python-embedded domain-specific language for hardware-accelerated machine learning, suitable for both interactive research and production. TensorFlow, which TensorFlow Eager extends, requires users to represent computations as dataflow graphs; this permits compiler optimizations and simplifies deployment but hinders rapid prototyping and run-time dynamism. TensorFlow Eager eliminates these usability costs without sacrificing the benefits furnished by graphs: It provides an imperative front-end to TensorFlow that executes operations immediately and a JIT tracer that translates Python functions composed of TensorFlow operations into executable dataflow graphs. TensorFlow Eager thus offers a multi-stage programming model that makes it easy to interpolate between imperative and staged execution in a single package.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge