A Near-Linear Time Approximation Algorithm for Beyond-Worst-Case Graph Clustering

We consider the semi-random graph model of [Makarychev, Makarychev and Vijayaraghavan, STOC'12], where, given a random bipartite graph with $\alpha$ edges and an unknown bipartition $(A, B)$ of the vertex set, an adversary can add arbitrary edges inside each community and remove arbitrary edges from the cut $(A, B)$ (i.e. all adversarial changes are \textit{monotone} with respect to the bipartition). For this model, a polynomial time algorithm is known to approximate the Balanced Cut problem up to value $O(\alpha)$ [MMV'12] as long as the cut $(A, B)$ has size $\Omega(\alpha)$. However, it consists of slow subroutines requiring optimal solutions for logarithmically many semidefinite programs. We study the fine-grained complexity of the problem and present the first near-linear time algorithm that achieves similar performances to that of [MMV'12]. Our algorithm runs in time $O(|V(G)|^{1+o(1)} + |E(G)|^{1+o(1)})$ and finds a balanced cut of value $O(\alpha)$. Our approach appears easily extendible to related problem, such as Sparsest Cut, and also yields an near-linear time $O(1)$-approximation to Dagupta's objective function for hierarchical clustering [Dasgupta, STOC'16] for the semi-random hierarchical stochastic block model inputs of [Cohen-Addad, Kanade, Mallmann-Trenn, Mathieu, JACM'19].

Beyond $1/2$-Approximation for Submodular Maximization on Massive Data Streams

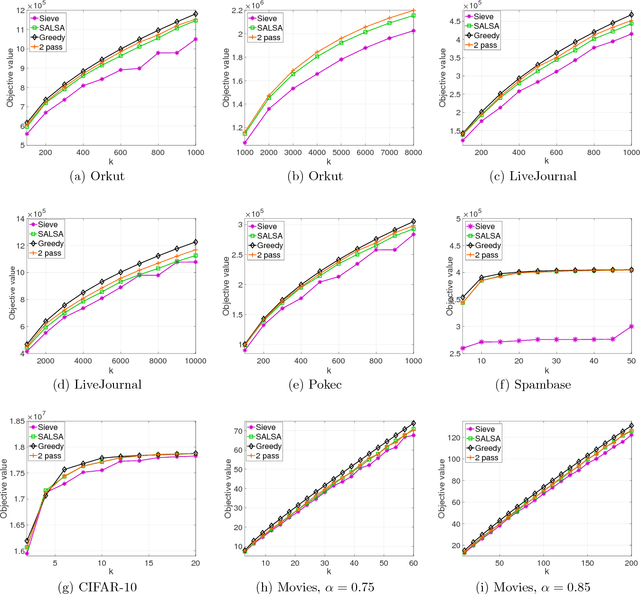
Many tasks in machine learning and data mining, such as data diversification, non-parametric learning, kernel machines, clustering etc., require extracting a small but representative summary from a massive dataset. Often, such problems can be posed as maximizing a submodular set function subject to a cardinality constraint. We consider this question in the streaming setting, where elements arrive over time at a fast pace and thus we need to design an efficient, low-memory algorithm. One such method, proposed by Badanidiyuru et al. (2014), always finds a $0.5$-approximate solution. Can this approximation factor be improved? We answer this question affirmatively by designing a new algorithm SALSA for streaming submodular maximization. It is the first low-memory, single-pass algorithm that improves the factor $0.5$, under the natural assumption that elements arrive in a random order. We also show that this assumption is necessary, i.e., that there is no such algorithm with better than $0.5$-approximation when elements arrive in arbitrary order. Our experiments demonstrate that SALSA significantly outperforms the state of the art in applications related to exemplar-based clustering, social graph analysis, and recommender systems.