Abhishek Tripathi
Demand Prediction and Placement Optimization for Electric Vehicle Charging Stations
Jul 13, 2016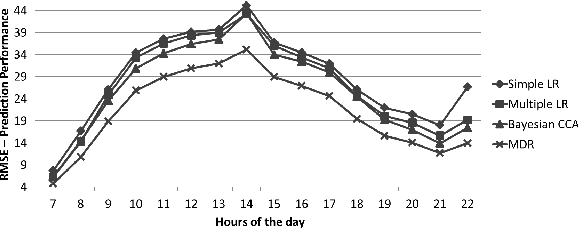

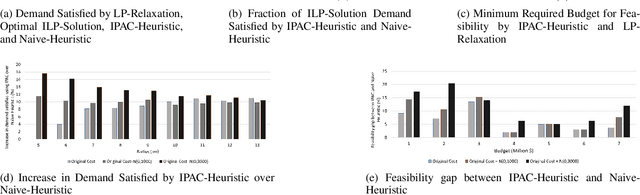
Abstract:Effective placement of charging stations plays a key role in Electric Vehicle (EV) adoption. In the placement problem, given a set of candidate sites, an optimal subset needs to be selected with respect to the concerns of both (a) the charging station service provider, such as the demand at the candidate sites and the budget for deployment, and (b) the EV user, such as charging station reachability and short waiting times at the station. This work addresses these concerns, making the following three novel contributions: (i) a supervised multi-view learning framework using Canonical Correlation Analysis (CCA) for demand prediction at candidate sites, using multiple datasets such as points of interest information, traffic density, and the historical usage at existing charging stations; (ii) a mixed-packing-and- covering optimization framework that models competing concerns of the service provider and EV users; (iii) an iterative heuristic to solve these problems by alternately invoking knapsack and set cover algorithms. The performance of the demand prediction model and the placement optimization heuristic are evaluated using real world data.
Probabilistic Dependency Networks for Prediction and Diagnostics
Aug 13, 2015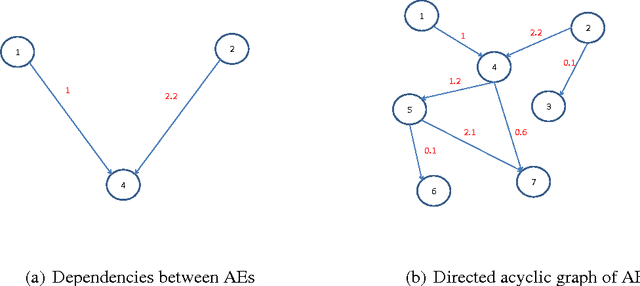
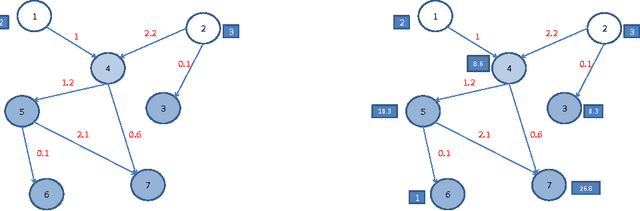
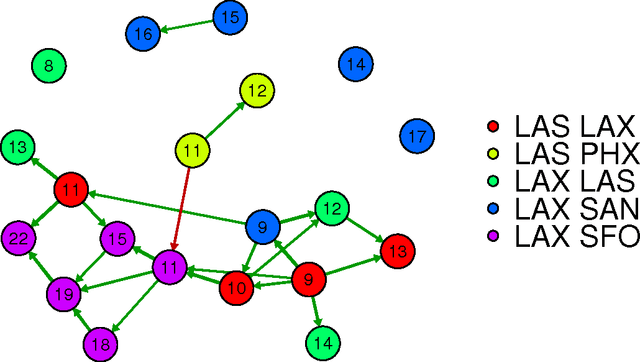
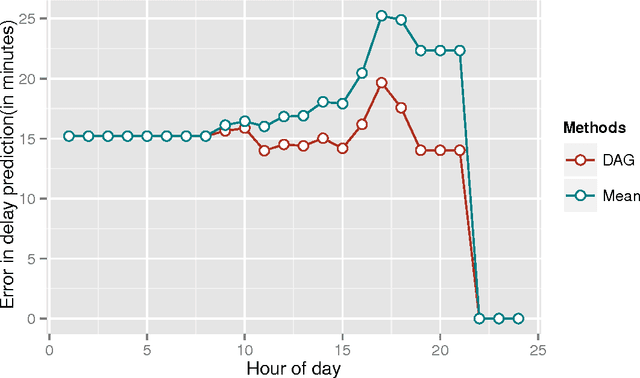
Abstract:Research in transportation frequently involve modelling and predicting attributes of events that occur at regular intervals. The event could be arrival of a bus at a bus stop, the volume of a traffic at a particular point, the demand at a particular bus stop etc. In this work, we propose a specific implementation of probabilistic graphical models to learn the probabilistic dependency between the events that occur in a network. A dependency graph is built from the past observed instances of the event and we use the graph to understand the causal effects of some events on others in the system. The dependency graph is also used to predict the attributes of future events and is shown to have a good prediction accuracy compared to the state of the art.
Group-sparse Embeddings in Collective Matrix Factorization
Feb 18, 2014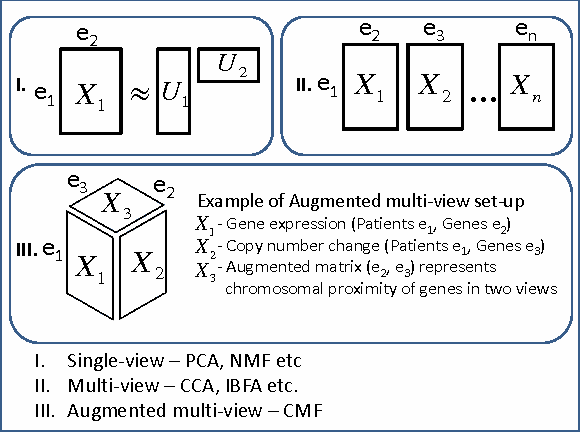
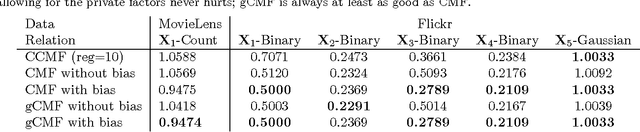
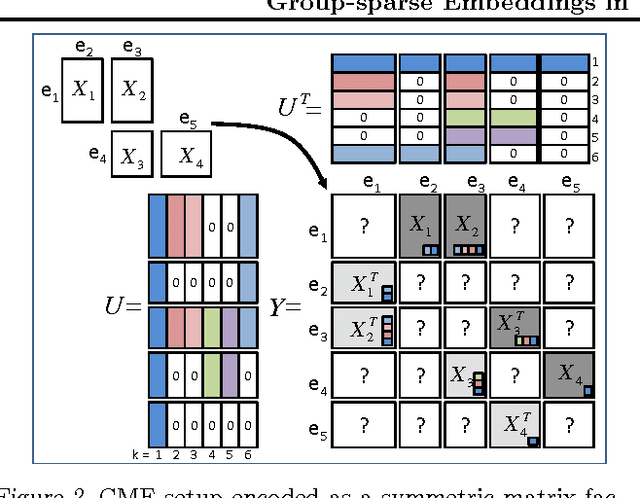
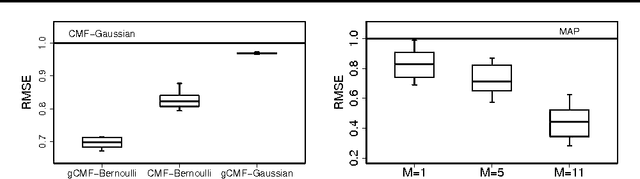
Abstract:CMF is a technique for simultaneously learning low-rank representations based on a collection of matrices with shared entities. A typical example is the joint modeling of user-item, item-property, and user-feature matrices in a recommender system. The key idea in CMF is that the embeddings are shared across the matrices, which enables transferring information between them. The existing solutions, however, break down when the individual matrices have low-rank structure not shared with others. In this work we present a novel CMF solution that allows each of the matrices to have a separate low-rank structure that is independent of the other matrices, as well as structures that are shared only by a subset of them. We compare MAP and variational Bayesian solutions based on alternating optimization algorithms and show that the model automatically infers the nature of each factor using group-wise sparsity. Our approach supports in a principled way continuous, binary and count observations and is efficient for sparse matrices involving missing data. We illustrate the solution on a number of examples, focusing in particular on an interesting use-case of augmented multi-view learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge