AMA-Bench: Evaluating Long-Horizon Memory for Agentic Applications

Large Language Models (LLMs) are deployed as autonomous agents in increasingly complex applications, where enabling long-horizon memory is critical for achieving strong performance. However, a significant gap exists between practical applications and current evaluation standards for agent memory: existing benchmarks primarily focus on dialogue-centric, human-agent interactions. In reality, agent memory consists of a continuous stream of agent-environment interactions that are primarily composed of machine-generated representations. To bridge this gap, we introduce AMA-Bench (Agent Memory with Any length), which evaluates long-horizon memory for LLMs in real agentic applications. It features two key components: (1) a set of real-world agentic trajectories across representative agentic applications, paired with expert-curated QA, and (2) a set of synthetic agentic trajectories that scale to arbitrary horizons, paired with rule-based QA. Our comprehensive study shows that existing memory systems underperform on AMA-Bench primarily because they lack causality and objective information and are constrained by the lossy nature of similarity-based retrieval employed by many memory systems. To address these limitations, we propose AMA-Agent, an effective memory system featuring a causality graph and tool-augmented retrieval. Our results demonstrate that AMA-Agent achieves 57.22% average accuracy on AMA-Bench, surpassing the strongest memory system baselines by 11.16%.

Towards Interpretable and Inference-Optimal COT Reasoning with Sparse Autoencoder-Guided Generation

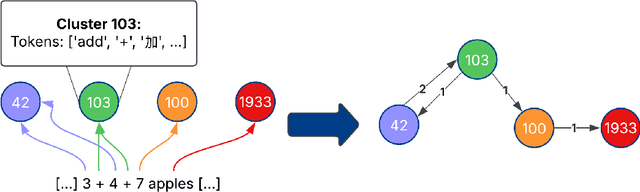
We propose a novel method that leverages sparse autoencoders (SAEs) and clustering techniques to analyze the internal token representations of large language models (LLMs) and guide generations in mathematical reasoning tasks. Our approach first trains an SAE to generate sparse vector representations for training tokens, then applies k-means clustering to construct a graph where vertices represent token clusters and weighted edges capture sequential token transitions. Using this graph, we define an edge-weight based reward function to quantify adherence to established reasoning traces, thereby identifying exploitative reasoning trajectories. Additionally, we measure generation diversity from clustering to assess the extent of exploration. Our findings indicate that balancing both exploitation and exploration is crucial for achieving high accuracy in mathematical reasoning tasks. During generation, the SAE can serve as a scalable reward model to guide generations, ensuring a balanced trade-off between exploitation and exploration. This prevents extreme behaviors in either direction, ultimately fostering a higher-quality reasoning process in LLMs.

TransientTables: Evaluating LLMs' Reasoning on Temporally Evolving Semi-structured Tables

Humans continuously make new discoveries, and understanding temporal sequence of events leading to these breakthroughs is essential for advancing science and society. This ability to reason over time allows us to identify future steps and understand the effects of financial and political decisions on our lives. However, large language models (LLMs) are typically trained on static datasets, limiting their ability to perform effective temporal reasoning. To assess the temporal reasoning capabilities of LLMs, we present the TRANSIENTTABLES dataset, which comprises 3,971 questions derived from over 14,000 tables, spanning 1,238 entities across multiple time periods. We introduce a template-based question-generation pipeline that harnesses LLMs to refine both templates and questions. Additionally, we establish baseline results using state-of-the-art LLMs to create a benchmark. We also introduce novel modeling strategies centered around task decomposition, enhancing LLM performance.

Exploring the Numerical Reasoning Capabilities of Language Models: A Comprehensive Analysis on Tabular Data

Numbers are crucial for various real-world domains such as finance, economics, and science. Thus, understanding and reasoning with numbers are essential skills for language models to solve different tasks. While different numerical benchmarks have been introduced in recent years, they are limited to specific numerical aspects mostly. In this paper, we propose a hierarchical taxonomy for numerical reasoning skills with more than ten reasoning types across four levels: representation, number sense, manipulation, and complex reasoning. We conduct a comprehensive evaluation of state-of-the-art models to identify reasoning challenges specific to them. Henceforth, we develop a diverse set of numerical probes employing a semi-automated approach. We focus on the tabular Natural Language Inference (TNLI) task as a case study and measure models' performance shifts. Our results show that no model consistently excels across all numerical reasoning types. Among the probed models, FlanT5 (few-/zero-shot) and GPT-3.5 (few-shot) demonstrate strong overall numerical reasoning skills compared to other models. Label-flipping probes indicate that models often exploit dataset artifacts to predict the correct labels.