Sample-Optimal Low-Rank Approximation of Distance Matrices
Paper and Code
Jun 02, 2019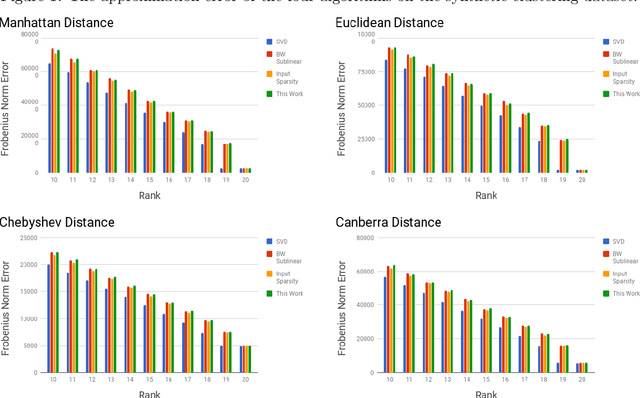
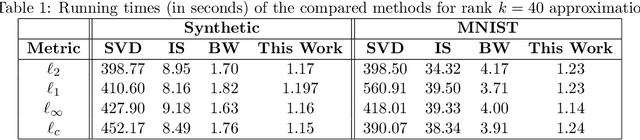
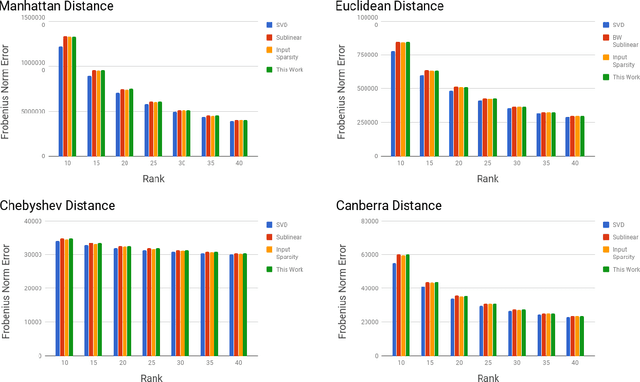
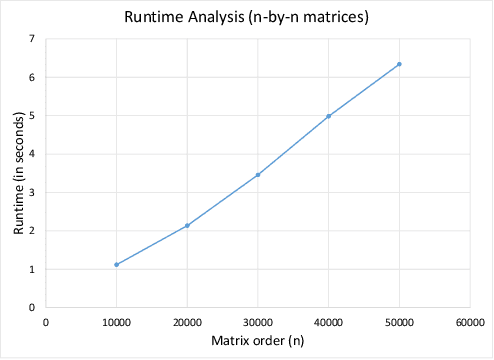
A distance matrix $A \in \mathbb R^{n \times m}$ represents all pairwise distances, $A_{ij}=\mathrm{d}(x_i,y_j)$, between two point sets $x_1,...,x_n$ and $y_1,...,y_m$ in an arbitrary metric space $(\mathcal Z, \mathrm{d})$. Such matrices arise in various computational contexts such as learning image manifolds, handwriting recognition, and multi-dimensional unfolding. In this work we study algorithms for low-rank approximation of distance matrices. Recent work by Bakshi and Woodruff (NeurIPS 2018) showed it is possible to compute a rank-$k$ approximation of a distance matrix in time $O((n+m)^{1+\gamma}) \cdot \mathrm{poly}(k,1/\epsilon)$, where $\epsilon>0$ is an error parameter and $\gamma>0$ is an arbitrarily small constant. Notably, their bound is sublinear in the matrix size, which is unachievable for general matrices. We present an algorithm that is both simpler and more efficient. It reads only $O((n+m) k/\epsilon)$ entries of the input matrix, and has a running time of $O(n+m) \cdot \mathrm{poly}(k,1/\epsilon)$. We complement the sample complexity of our algorithm with a matching lower bound on the number of entries that must be read by any algorithm. We provide experimental results to validate the approximation quality and running time of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge