Communication Efficient Decentralized Training with Multiple Local Updates

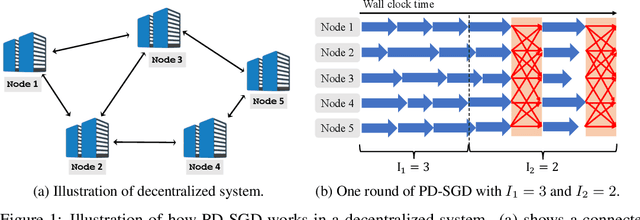
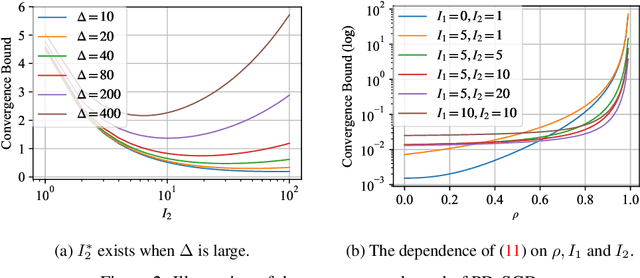
Decentralized optimization has been demonstrated to be very useful in machine learning. This work studies the communication-efficiency issue in decentralized optimization. We analyze the Periodic Decentralized Stochastic Gradient Descent (PD-SGD) algorithm, a straightforward combination of federated averaging and decentralized SGD. For the setting of for non-convex objective and non-identically distributed data, we prove that PD-SGD converges to a critical point. In particular, the number of local SGDs trades off communication and local computation. From an algorithmic perspective, we analyze a novel version of PD-SGD, which alternates between multiple local updates and multiple decentralized SGDs. We also show that when we periodically shrink the length of local updates, this generalized PD-SGD can better balance the communication-convergence trade-off both theoretically and empirically.