Active Finite Reward Automaton Inference and Reinforcement Learning Using Queries and Counterexamples

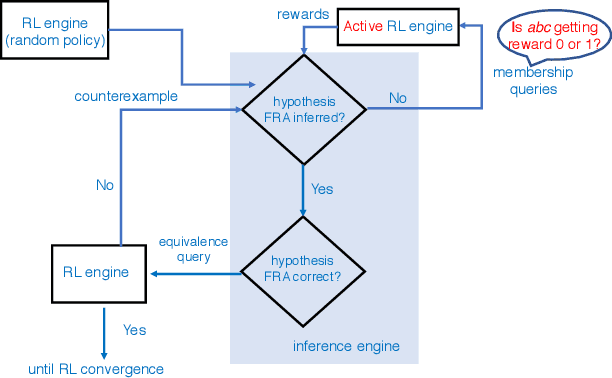
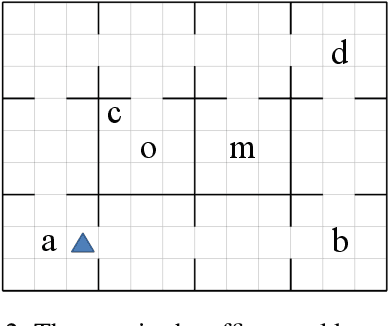
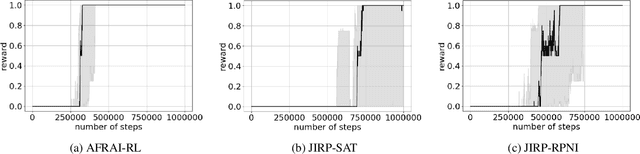
Despite the fact that deep reinforcement learning (RL) has surpassed human-level performances in various tasks, it still has several fundamental challenges such as extensive data requirement and lack of interpretability. We investigate the RL problem with non-Markovian reward functions to address such challenges. We enable an RL agent to extract high-level knowledge in the form of finite reward automata, a type of Mealy machines that encode non-Markovian reward functions. The finite reward automata can be converted to deterministic finite state machines, which can be further translated to regular expressions. Thus, this representation is more interpretable than other forms of knowledge representation such as neural networks. We propose an active learning approach that iteratively infers finite reward automata and performs RL (specifically, q-learning) based on the inferred finite reward automata. The inference method is inspired by the L* learning algorithm, and modified in the framework of RL. We maintain two different q-functions, one for answering the membership queries in the L* learning algorithm and the other one for obtaining optimal policies for the inferred finite reward automaton. The experiments show that the proposed approach converges to optimal policies in at most 50% of the training steps as in the two state-of-the-art baselines.