Parameterized Verification of Algorithms for Oblivious Robots on a Ring

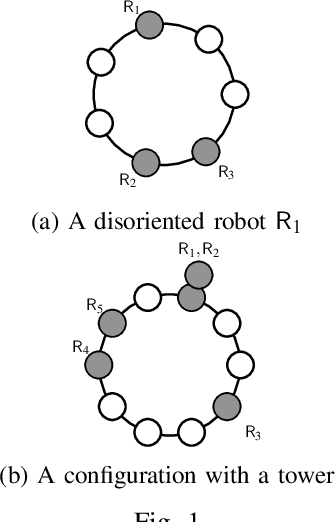
We study verification problems for autonomous swarms of mobile robots that self-organize and cooperate to solve global objectives. In particular, we focus in this paper on the model proposed by Suzuki and Yamashita of anonymous robots evolving in a discrete space with a finite number of locations (here, a ring). A large number of algorithms have been proposed working for rings whose size is not a priori fixed and can be hence considered as a parameter. Handmade correctness proofs of these algorithms have been shown to be error-prone, and recent attention had been given to the application of formal methods to automatically prove those. Our work is the first to study the verification problem of such algorithms in the parameter-ized case. We show that safety and reachability problems are undecidable for robots evolving asynchronously. On the positive side, we show that safety properties are decidable in the synchronous case, as well as in the asynchronous case for a particular class of algorithms. Several properties on the protocol can be decided as well. Decision procedures rely on an encoding in Presburger arithmetics formulae that can be verified by an SMT-solver. Feasibility of our approach is demonstrated by the encoding of several case studies.

Emergent velocity agreement in robot networks

In this paper we propose and prove correct a new self-stabilizing velocity agreement (flocking) algorithm for oblivious and asynchronous robot networks. Our algorithm allows a flock of uniform robots to follow a flock head emergent during the computation whatever its direction in plane. Robots are asynchronous, oblivious and do not share a common coordinate system. Our solution includes three modules architectured as follows: creation of a common coordinate system that also allows the emergence of a flock-head, setting up the flock pattern and moving the flock. The novelty of our approach steams in identifying the necessary conditions on the flock pattern placement and the velocity of the flock-head (rotation, translation or speed) that allow the flock to both follow the exact same head and to preserve the flock pattern. Additionally, our system is self-healing and self-stabilizing. In the event of the head leave (the leading robot disappears or is damaged and cannot be recognized by the other robots) the flock agrees on another head and follows the trajectory of the new head. Also, robots are oblivious (they do not recall the result of their previous computations) and we make no assumption on their initial position. The step complexity of our solution is O(n).

RoboCast: Asynchronous Communication in Robot Networks

This paper introduces the \emph{RoboCast} communication abstraction. The RoboCast allows a swarm of non oblivious, anonymous robots that are only endowed with visibility sensors and do not share a common coordinate system, to asynchronously exchange information. We propose a generic framework that covers a large class of asynchronous communication algorithms and show how our framework can be used to implement fundamental building blocks in robot networks such as gathering or stigmergy. In more details, we propose a RoboCast algorithm that allows robots to broadcast their local coordinate systems to each others. Our algorithm is further refined with a local collision avoidance scheme. Then, using the RoboCast primitive, we propose algorithms for deterministic asynchronous gathering and binary information exchange.

Byzantine Convergence in Robots Networks: The Price of Asynchrony

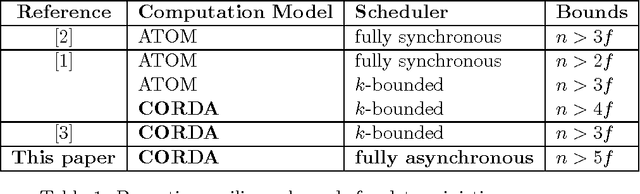
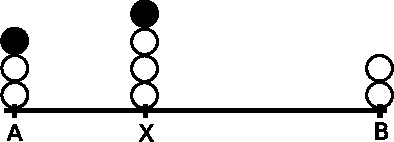
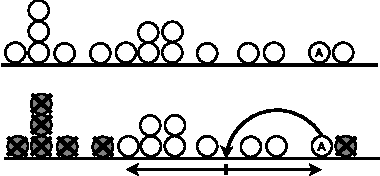
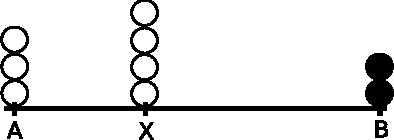
We study the convergence problem in fully asynchronous, uni-dimensional robot networks that are prone to Byzantine (i.e. malicious) failures. In these settings, oblivious anonymous robots with arbitrary initial positions are required to eventually converge to an a apriori unknown position despite a subset of them exhibiting Byzantine behavior. Our contribution is twofold. We propose a deterministic algorithm that solves the problem in the most generic settings: fully asynchronous robots that operate in the non-atomic CORDA model. Our algorithm provides convergence in 5f+1-sized networks where f is the upper bound on the number of Byzantine robots. Additionally, we prove that 5f+1 is a lower bound whenever robot scheduling is fully asynchronous. This constrasts with previous results in partially synchronous robots networks, where 3f+1 robots are necessary and sufficient.

Optimal Byzantine Resilient Convergence in Asynchronous Robot Networks

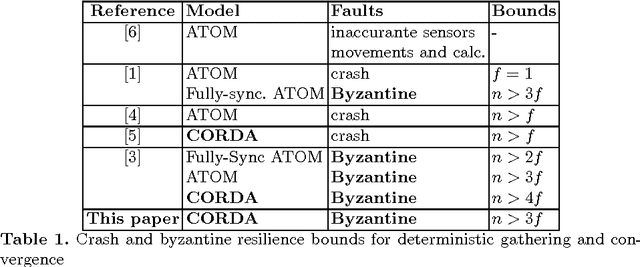
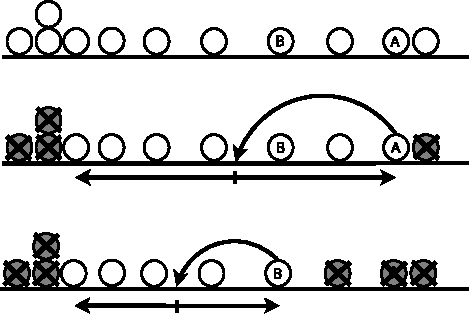
We propose the first deterministic algorithm that tolerates up to $f$ byzantine faults in $3f+1$-sized networks and performs in the asynchronous CORDA model. Our solution matches the previously established lower bound for the semi-synchronous ATOM model on the number of tolerated Byzantine robots. Our algorithm works under bounded scheduling assumptions for oblivious robots moving in a uni-dimensional space.

Optimal byzantine resilient convergence in oblivious robot networks

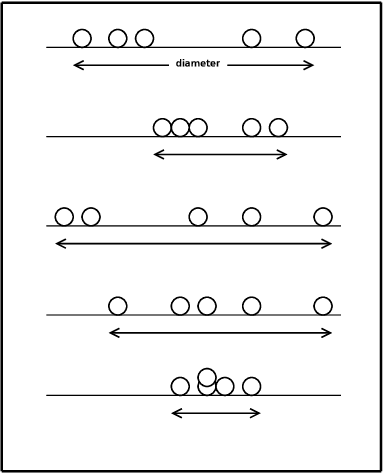
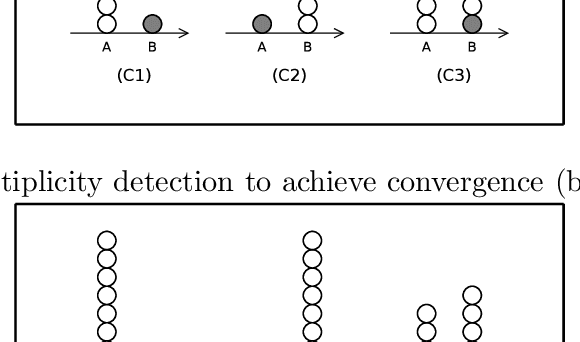
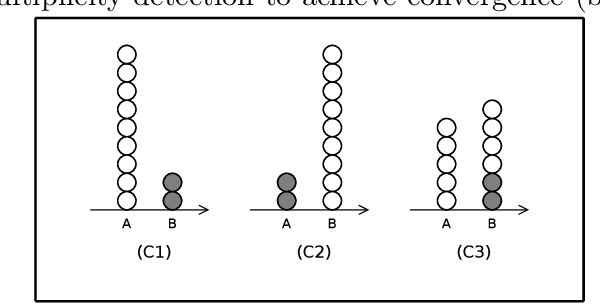
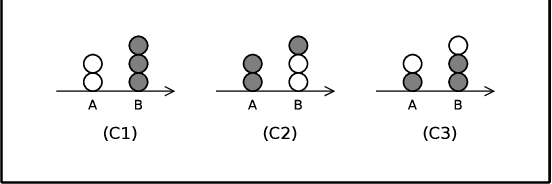
Given a set of robots with arbitrary initial location and no agreement on a global coordinate system, convergence requires that all robots asymptotically approach the exact same, but unknown beforehand, location. Robots are oblivious-- they do not recall the past computations -- and are allowed to move in a one-dimensional space. Additionally, robots cannot communicate directly, instead they obtain system related information only via visual sensors. We draw a connection between the convergence problem in robot networks, and the distributed \emph{approximate agreement} problem (that requires correct processes to decide, for some constant $\epsilon$, values distance $\epsilon$ apart and within the range of initial proposed values). Surprisingly, even though specifications are similar, the convergence implementation in robot networks requires specific assumptions about synchrony and Byzantine resilience. In more details, we prove necessary and sufficient conditions for the convergence of mobile robots despite a subset of them being Byzantine (i.e. they can exhibit arbitrary behavior). Additionally, we propose a deterministic convergence algorithm for robot networks and analyze its correctness and complexity in various synchrony settings. The proposed algorithm tolerates f Byzantine robots for (2f+1)-sized robot networks in fully synchronous networks, (3f+1)-sized in semi-synchronous networks. These bounds are optimal for the class of cautious algorithms, which guarantee that correct robots always move inside the range of positions of the correct robots.