Benchmarking Uncertainty Quantification of Plug-and-Play Diffusion Priors for Inverse Problems Solving

Plug-and-play diffusion priors (PnPDP) have become a powerful paradigm for solving inverse problems in scientific and engineering domains. Yet, current evaluations of reconstruction quality emphasize point-estimate accuracy metrics on a single sample, which do not reflect the stochastic nature of PnPDP solvers and the intrinsic uncertainty of inverse problems, critical for scientific tasks. This creates a fundamental mismatch: in inverse problems, the desired output is typically a posterior distribution and most PnPDP solvers induce a distribution over reconstructions, but existing benchmarks only evaluate a single reconstruction, ignoring distributional characterization such as uncertainty. To address this gap, we conduct a systematic study to benchmark the uncertainty quantification (UQ) of existing diffusion inverse solvers. Specifically, we design a rigorous toy model simulation to evaluate the uncertainty behavior of various PnPDP solvers, and propose a UQ-driven categorization. Through extensive experiments on toy simulations and diverse real-world scientific inverse problems, we observe uncertainty behaviors consistent with our taxonomy and theoretical justification, providing new insights for evaluating and understanding the uncertainty for PnPDPs.

Windowed total variation denoising and noise variance monitoring

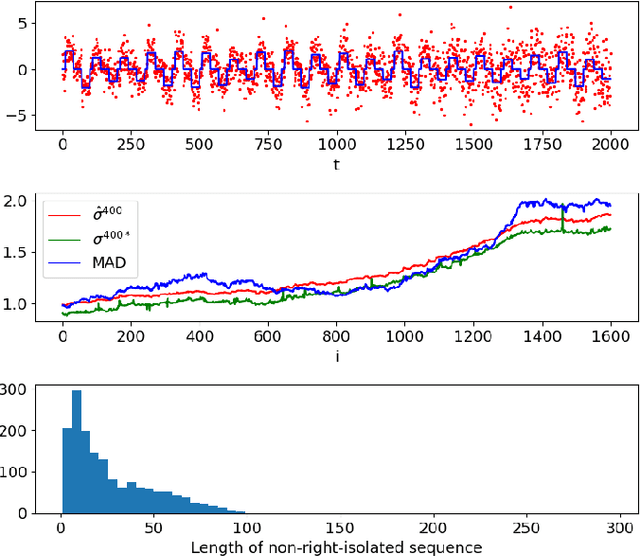
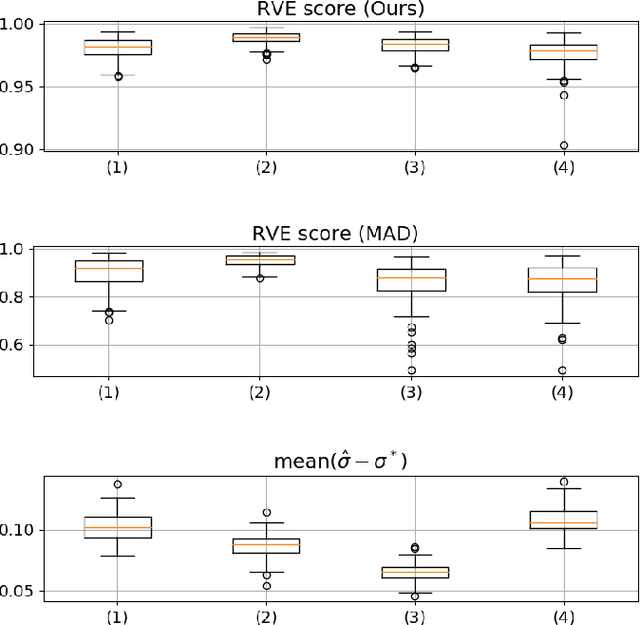
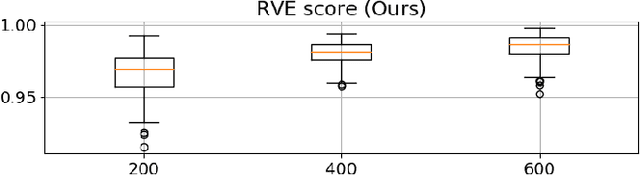
We proposed a real time Total-Variation denosing method with an automatic choice of hyper-parameter $\lambda$, and the good performance of this method provides a large application field. In this article, we adapt the developed method to the non stationary signal in using the sliding window, and propose a noise variance monitoring method. The simulated results show that our proposition follows well the variation of noise variance.