EM's Convergence in Gaussian Latent Tree Models

We study the optimization landscape of the log-likelihood function and the convergence of the Expectation-Maximization (EM) algorithm in latent Gaussian tree models, i.e. tree-structured Gaussian graphical models whose leaf nodes are observable and non-leaf nodes are unobservable. We show that the unique non-trivial stationary point of the population log-likelihood is its global maximum, and establish that the expectation-maximization algorithm is guaranteed to converge to it in the single latent variable case. Our results for the landscape of the log-likelihood function in general latent tree models provide support for the extensive practical use of maximum likelihood based-methods in this setting. Our results for the EM algorithm extend an emerging line of work on obtaining global convergence guarantees for this celebrated algorithm. We show our results for the non-trivial stationary points of the log-likelihood by arguing that a certain system of polynomial equations obtained from the EM updates has a unique non-trivial solution. The global convergence of the EM algorithm follows by arguing that all trivial fixed points are higher-order saddle points.

Score-Guided Intermediate Layer Optimization: Fast Langevin Mixing for Inverse Problems

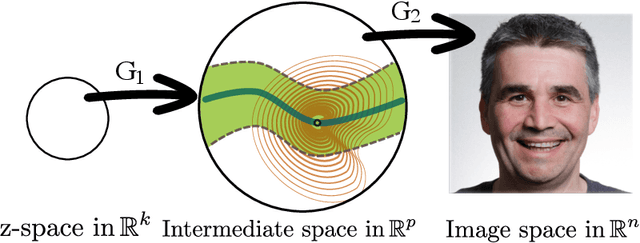
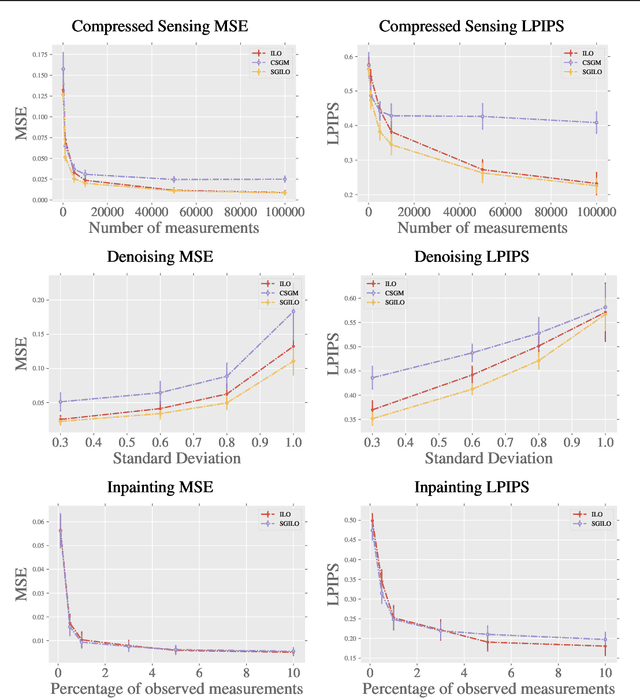
We prove fast mixing and characterize the stationary distribution of the Langevin Algorithm for inverting random weighted DNN generators. This result extends the work of Hand and Voroninski from efficient inversion to efficient posterior sampling. In practice, to allow for increased expressivity, we propose to do posterior sampling in the latent space of a pre-trained generative model. To achieve that, we train a score-based model in the latent space of a StyleGAN-2 and we use it to solve inverse problems. Our framework, Score-Guided Intermediate Layer Optimization (SGILO), extends prior work by replacing the sparsity regularization with a generative prior in the intermediate layer. Experimentally, we obtain significant improvements over the previous state-of-the-art, especially in the low measurement regime.

Smoothed Online Learning is as Easy as Statistical Learning

Much of modern learning theory has been split between two regimes: the classical offline setting, where data arrive independently, and the online setting, where data arrive adversarially. While the former model is often both computationally and statistically tractable, the latter requires no distributional assumptions. In an attempt to achieve the best of both worlds, previous work proposed the smooth online setting where each sample is drawn from an adversarially chosen distribution, which is smooth, i.e., it has a bounded density with respect to a fixed dominating measure. We provide tight bounds on the minimax regret of learning a nonparametric function class, with nearly optimal dependence on both the horizon and smoothness parameters. Furthermore, we provide the first oracle-efficient, no-regret algorithms in this setting. In particular, we propose an oracle-efficient improper algorithm whose regret achieves optimal dependence on the horizon and a proper algorithm requiring only a single oracle call per round whose regret has the optimal horizon dependence in the classification setting and is sublinear in general. Both algorithms have exponentially worse dependence on the smoothness parameter of the adversary than the minimax rate. We then prove a lower bound on the oracle complexity of any proper learning algorithm, which matches the oracle-efficient upper bounds up to a polynomial factor, thus demonstrating the existence of a statistical-computational gap in smooth online learning. Finally, we apply our results to the contextual bandit setting to show that if a function class is learnable in the classical setting, then there is an oracle-efficient, no-regret algorithm for contextual bandits in the case that contexts arrive in a smooth manner.

Statistical Estimation from Dependent Data

We consider a general statistical estimation problem wherein binary labels across different observations are not independent conditioned on their feature vectors, but dependent, capturing settings where e.g. these observations are collected on a spatial domain, a temporal domain, or a social network, which induce dependencies. We model these dependencies in the language of Markov Random Fields and, importantly, allow these dependencies to be substantial, i.e do not assume that the Markov Random Field capturing these dependencies is in high temperature. As our main contribution we provide algorithms and statistically efficient estimation rates for this model, giving several instantiations of our bounds in logistic regression, sparse logistic regression, and neural network settings with dependent data. Our estimation guarantees follow from novel results for estimating the parameters (i.e. external fields and interaction strengths) of Ising models from a {\em single} sample. {We evaluate our estimation approach on real networked data, showing that it outperforms standard regression approaches that ignore dependencies, across three text classification datasets: Cora, Citeseer and Pubmed.}

Majorizing Measures, Sequential Complexities, and Online Learning

We introduce the technique of generic chaining and majorizing measures for controlling sequential Rademacher complexity. We relate majorizing measures to the notion of fractional covering numbers, which we show to be dominated in terms of sequential scale-sensitive dimensions in a horizon-independent way, and, under additional complexity assumptions establish a tight control on worst-case sequential Rademacher complexity in terms of the integral of sequential scale-sensitive dimension. Finally, we establish a tight contraction inequality for worst-case sequential Rademacher complexity. The above constitutes the resolution of a number of outstanding open problems in extending the classical theory of empirical processes to the sequential case, and, in turn, establishes sharp results for online learning.

Adversarial Laws of Large Numbers and Optimal Regret in Online Classification

Laws of large numbers guarantee that given a large enough sample from some population, the measure of any fixed sub-population is well-estimated by its frequency in the sample. We study laws of large numbers in sampling processes that can affect the environment they are acting upon and interact with it. Specifically, we consider the sequential sampling model proposed by Ben-Eliezer and Yogev (2020), and characterize the classes which admit a uniform law of large numbers in this model: these are exactly the classes that are \emph{online learnable}. Our characterization may be interpreted as an online analogue to the equivalence between learnability and uniform convergence in statistical (PAC) learning. The sample-complexity bounds we obtain are tight for many parameter regimes, and as an application, we determine the optimal regret bounds in online learning, stated in terms of \emph{Littlestone's dimension}, thus resolving the main open question from Ben-David, P\'al, and Shalev-Shwartz (2009), which was also posed by Rakhlin, Sridharan, and Tewari (2015).

A bounded-noise mechanism for differential privacy

Answering multiple counting queries is one of the best-studied problems in differential privacy. Its goal is to output an approximation of the average $\frac{1}{n}\sum_{i=1}^n \vec{x}^{(i)}$ of vectors $\vec{x}^{(i)} \in [0,1]^k$, while preserving the privacy with respect to any $\vec{x}^{(i)}$. We present an $(\epsilon,\delta)$-private mechanism with optimal $\ell_\infty$ error for most values of $\delta$. This result settles the conjecture of Steinke and Ullman [2020] for the these values of $\delta$. Our algorithm adds independent noise of bounded magnitude to each of the $k$ coordinates, while prior solutions relied on unbounded noise such as the Laplace and Gaussian mechanisms.

Estimating Ising Models from One Sample

Given one sample $X \in \{\pm 1\}^n$ from an Ising model $\Pr[X=x]\propto \exp(x^\top J x/2)$, whose interaction matrix satisfies $J:= \sum_{i=1}^k \beta_i J_i$ for some known matrices $J_i$ and some unknown parameters $\beta_i$, we study whether $J$ can be estimated to high accuracy. Assuming that each node of the Ising model has bounded total interaction with the other nodes, i.e. $\|J\|_{\infty} \le O(1)$, we provide a computationally efficient estimator $\hat{J}$ with the high probability guarantee $\|\hat{J} -J\|_F \le \widetilde O(\sqrt{k})$, where $\|J\|_F$ can be as high as $\Omega(\sqrt{n})$. Our guarantee is tight when the interaction strengths are sufficiently low. An example application of our result is in social networks, wherein nodes make binary choices, $x_1,\ldots,x_n$, which may be influenced at varying strengths $\beta_i$ by different networks $J_i$ in which these nodes belong. By observing a single snapshot of the nodes' behaviors the goal is to learn the combined correlation structure. When $k=1$ and a single parameter is to be inferred, we further show $|\hat{\beta}_1 - \beta_1| \le \widetilde O(F(\beta_1J_1)^{-1/2})$, where $F(\beta_1J_1)$ is the log-partition function of the model. This was proved in prior work under additional assumptions. We generalize these results to any setting. While our guarantees aim both high and low temperature regimes, our proof relies on sparsifying the correlation network by conditioning on subsets of the variables, such that the unconditioned variables satisfy Dobrushin's condition, i.e. a high temperature condition which allows us to apply stronger concentration inequalities. We use this to prove concentration and anti-concentration properties of the Ising model, and we believe this sparsification result has applications beyond the scope of this paper as well.

PAC learning with stable and private predictions

We study binary classification algorithms for which the prediction on any point is not too sensitive to individual examples in the dataset. Specifically, we consider the notions of uniform stability (Bousquet and Elisseeff, 2001) and prediction privacy (Dwork and Feldman, 2018). Previous work on these notions shows how they can be achieved in the standard PAC model via simple aggregation of models trained on disjoint subsets of data. Unfortunately, this approach leads to a significant overhead in terms of sample complexity. Here we demonstrate several general approaches to stable and private prediction that either eliminate or significantly reduce the overhead. Specifically, we demonstrate that for any class $C$ of VC dimension $d$ there exists a $\gamma$-uniformly stable algorithm for learning $C$ with excess error $\alpha$ using $\tilde O(d/(\alpha\gamma) + d/\alpha^2)$ samples. We also show that this bound is nearly tight. For $\epsilon$-differentially private prediction we give two new algorithms: one using $\tilde O(d/(\alpha^2\epsilon))$ samples and another one using $\tilde O(d^2/(\alpha\epsilon) + d/\alpha^2)$ samples. The best previously known bounds for these problems are $O(d/(\alpha^2\gamma))$ and $O(d/(\alpha^3\epsilon))$, respectively.

Interaction is necessary for distributed learning with privacy or communication constraints

Local differential privacy (LDP) is a model where users send privatized data to an untrusted central server whose goal it to solve some data analysis task. In the non-interactive version of this model the protocol consists of a single round in which a server sends requests to all users then receives their responses. This version is deployed in industry due to its practical advantages and has attracted significant research interest. Our main result is an exponential lower bound on the number of samples necessary to solve the standard task of learning a large-margin linear separator in the non-interactive LDP model. Via a standard reduction this lower bound implies an exponential lower bound for stochastic convex optimization and specifically, for learning linear models with a convex, Lipschitz and smooth loss. These results answer the questions posed in \citep{SmithTU17,DanielyF18}. Our lower bound relies on a new technique for constructing pairs of distributions with nearly matching moments but whose supports can be nearly separated by a large margin hyperplane. These lower bounds also hold in the model where communication from each user is limited and follow from a lower bound on learning using non-adaptive \emph{statistical queries}.