A Lipschitz spaces view of infinitely wide shallow neural networks

We revisit the mean field parametrization of shallow neural networks, using signed measures on unbounded parameter spaces and duality pairings that take into account the regularity and growth of activation functions. This setting directly leads to the use of unbalanced Kantorovich-Rubinstein norms defined by duality with Lipschitz functions, and of spaces of measures dual to those of continuous functions with controlled growth. These allow to make transparent the need for total variation and moment bounds or penalization to obtain existence of minimizers of variational formulations, under which we prove a compactness result in strong Kantorovich-Rubinstein norm, and in the absence of which we show several examples demonstrating undesirable behavior. Further, the Kantorovich-Rubinstein setting enables us to combine the advantages of a completely linear parametrization and ensuing reproducing kernel Banach space framework with optimal transport insights. We showcase this synergy with representer theorems and uniform large data limits for empirical risk minimization, and in proposed formulations for distillation and fusion applications.

Inverse Problems with Learned Forward Operators

Solving inverse problems requires knowledge of the forward operator, but accurate models can be computationally expensive and hence cheaper variants are desired that do not compromise reconstruction quality. This chapter reviews reconstruction methods in inverse problems with learned forward operators that follow two different paradigms. The first one is completely agnostic to the forward operator and learns its restriction to the subspace spanned by the training data. The framework of regularisation by projection is then used to find a reconstruction. The second one uses a simplified model of the physics of the measurement process and only relies on the training data to learn a model correction. We present the theory of these two approaches and compare them numerically. A common theme emerges: both methods require, or at least benefit from, training data not only for the forward operator, but also for its adjoint.

Unsupervised Learning of the Total Variation Flow

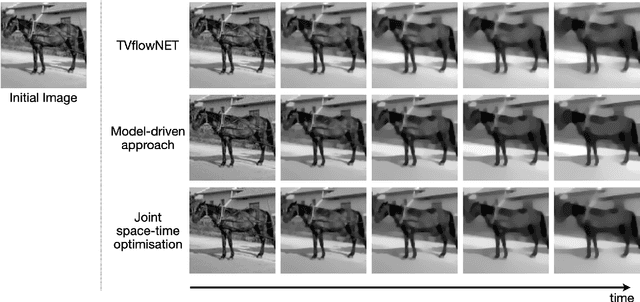
The total variation (TV) flow generates a scale-space representation of an image based on the TV functional. This gradient flow observes desirable features for images such as sharp edges and enables spectral, scale, and texture analysis. The standard numerical approach for TV flow requires solving multiple non-smooth optimisation problems. Even with state-of-the-art convex optimisation techniques, this is often prohibitively expensive and strongly motivates the use of alternative, faster approaches. Inspired by and extending the framework of physics-informed neural networks (PINNs), we propose the TVflowNET, a neural network approach to compute the solution of the TV flow given an initial image and a time instance. We significantly speed up the computation time by more than one order of magnitude and show that the TVflowNET approximates the TV flow solution with high fidelity. This is a preliminary report, more details are to follow.

Image reconstruction in light-sheet microscopy: spatially varying deconvolution and mixed noise

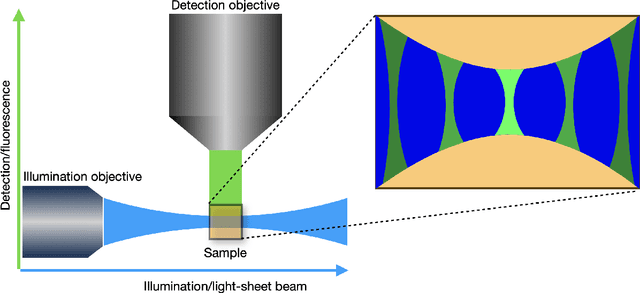
We study the problem of deconvolution for light-sheet microscopy, where the data is corrupted by spatially varying blur and a combination of Poisson and Gaussian noise. The spatial variation of the point spread function (PSF) of a light-sheet microscope is determined by the interaction between the excitation sheet and the detection objective PSF. First, we introduce a model of the image formation process that incorporates this interaction, therefore capturing the main characteristics of this imaging modality. Then, we formulate a variational model that accounts for the combination of Poisson and Gaussian noise through a data fidelity term consisting of the infimal convolution of the single noise fidelities, first introduced in L. Calatroni et al. "Infimal convolution of data discrepancies for mixed noise removal", SIAM Journal on Imaging Sciences 10.3 (2017), 1196-1233. We establish convergence rates in a Bregman distance under a source condition for the infimal convolution fidelity and a discrepancy principle for choosing the value of the regularisation parameter. The inverse problem is solved by applying the primal-dual hybrid gradient (PDHG) algorithm in a novel way. Finally, numerical experiments performed on both simulated and real data show superior reconstruction results in comparison with other methods.

Two-layer neural networks with values in a Banach space

We study two-layer neural networks whose domain and range are Banach spaces with separable preduals. In addition, we assume that the image space is equipped with a partial order, i.e. it is a Riesz space. As the nonlinearity we choose the lattice operation of taking the positive part; in case of $\mathbb R^d$-valued neural networks this corresponds to the ReLU activation function. We prove inverse and direct approximation theorems with Monte-Carlo rates, extending existing results for the finite-dimensional case. In the second part of the paper, we consider training such networks using a finite amount of noisy observations from the regularisation theory viewpoint. We discuss regularity conditions known as source conditions and obtain convergence rates in a Bregman distance in the regime when both the noise level goes to zero and the number of samples goes to infinity at appropriate rates.

Deeply Learned Spectral Total Variation Decomposition

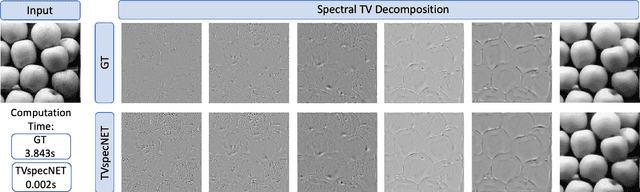
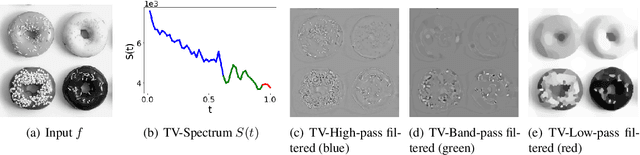
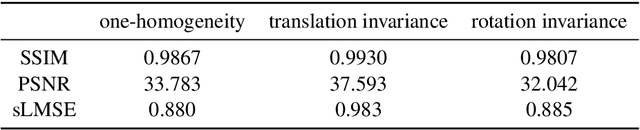
Non-linear spectral decompositions of images based on one-homogeneous functionals such as total variation have gained considerable attention in the last few years. Due to their ability to extract spectral components corresponding to objects of different size and contrast, such decompositions enable filtering, feature transfer, image fusion and other applications. However, obtaining this decomposition involves solving multiple non-smooth optimisation problems and is therefore computationally highly intensive. In this paper, we present a neural network approximation of a non-linear spectral decomposition. We report up to four orders of magnitude ($\times 10,000$) speedup in processing of mega-pixel size images, compared to classical GPU implementations. Our proposed network, TVSpecNET, is able to implicitly learn the underlying PDE and, despite being entirely data driven, inherits invariances of the model based transform. To the best of our knowledge, this is the first approach towards learning a non-linear spectral decomposition of images. Not only do we gain a staggering computational advantage, but this approach can also be seen as a step towards studying neural networks that can decompose an image into spectral components defined by a user rather than a handcrafted functional.

A total variation based regularizer promoting piecewise-Lipschitz reconstructions

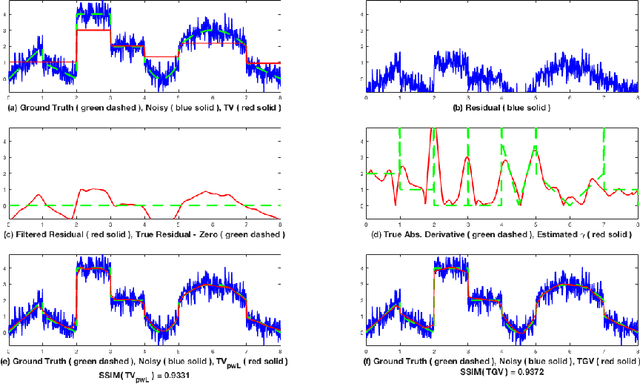
We introduce a new regularizer in the total variation family that promotes reconstructions with a given Lipschitz constant (which can also vary spatially). We prove regularizing properties of this functional and investigate its connections to total variation and infimal convolution type regularizers TVLp and, in particular, establish topological equivalence. Our numerical experiments show that the proposed regularizer can achieve similar performance as total generalized variation while having the advantage of a very intuitive interpretation of its free parameter, which is just a local estimate of the norm of the gradient. It also provides a natural approach to spatially adaptive regularization.

Image reconstruction with imperfect forward models and applications in deblurring

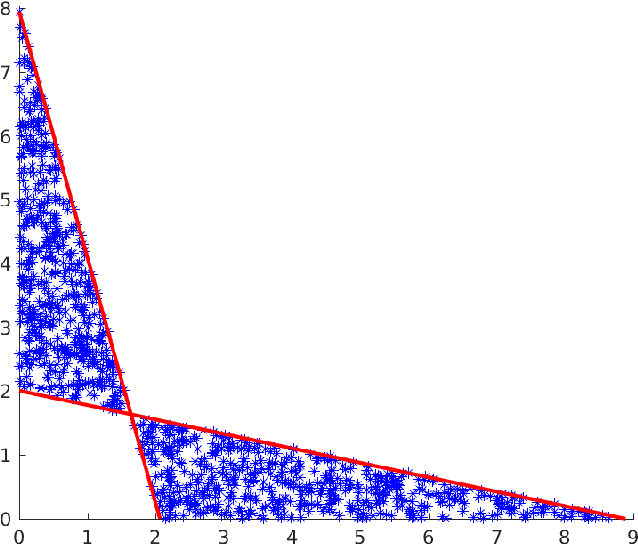
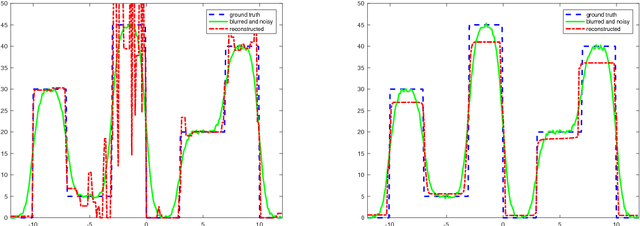
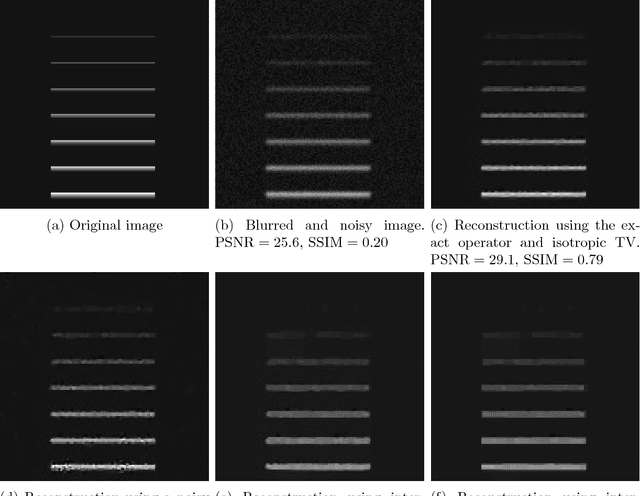
We present and analyse an approach to image reconstruction problems with imperfect forward models based on partially ordered spaces - Banach lattices. In this approach, errors in the data and in the forward models are described using order intervals. The method can be characterised as the lattice analogue of the residual method, where the feasible set is defined by linear inequality constraints. The study of this feasible set is the main contribution of this paper. Convexity of this feasible set is examined in several settings and modifications for introducing additional information about the forward operator are considered. Numerical examples demonstrate the performance of the method in deblurring with errors in the blurring kernel.

Diffusion tensor imaging with deterministic error bounds

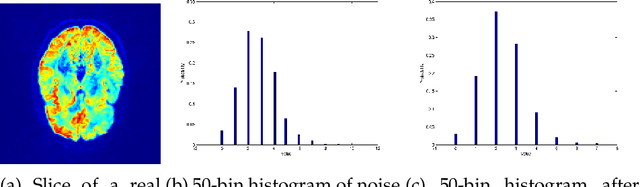
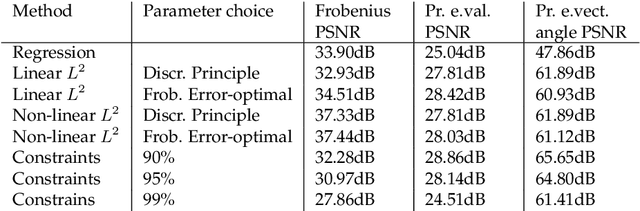
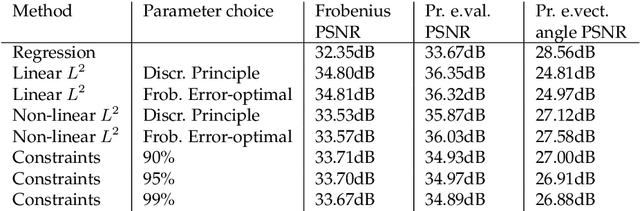
Errors in the data and the forward operator of an inverse problem can be handily modelled using partial order in Banach lattices. We present some existing results of the theory of regularisation in this novel framework, where errors are represented as bounds by means of the appropriate partial order. We apply the theory to Diffusion Tensor Imaging, where correct noise modelling is challenging: it involves the Rician distribution and the nonlinear Stejskal-Tanner equation. Linearisation of the latter in the statistical framework would complicate the noise model even further. We avoid this using the error bounds approach, which preserves simple error structure under monotone transformations.