From Drinking Philosophers to Wandering Robots

In this paper, we consider the multi-robot path execution problem where a group of robots move on predefined paths from their initial to target positions while avoiding collisions and deadlocks in the face of asynchrony. We first show that this problem can be reformulated as a distributed resource allocation problem and, in particular, as an instance of the well-known Drinking Philosophers Problem (DrPP). By careful construction of the drinking sessions capturing shared resources, we show that any existing solutions to DrPP can be used to design robot control policies that are collectively collision and deadlock-free. We then propose modifications to an existing DrPP algorithm to allow more concurrent behavior, and provide conditions under which our method is deadlock-free. Our method do not require robots to know or to estimate the speed profiles of other robots, and results in distributed control policies. We demonstrate the efficacy of our method on simulation examples, which show competitive performance against the state-of-the-art.

Multirobot Coordination with Counting Temporal Logics

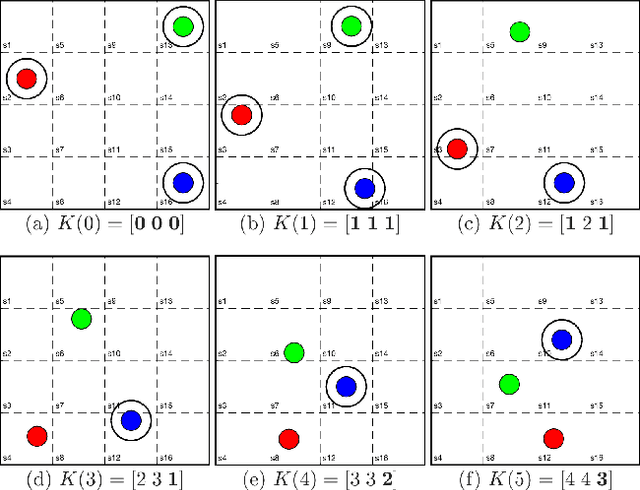
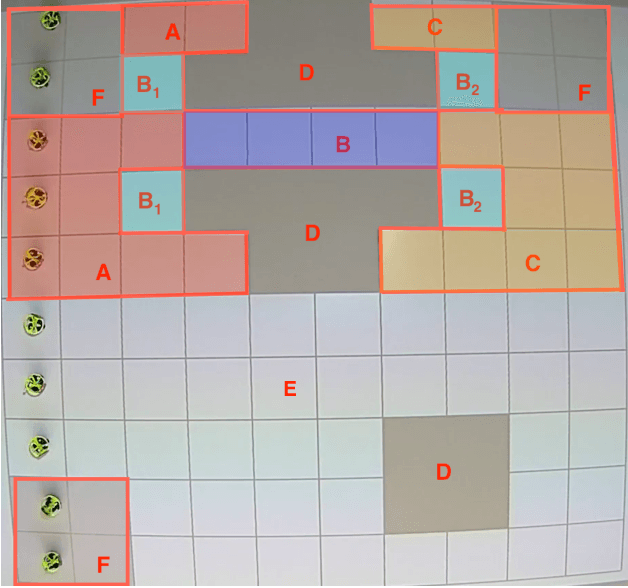
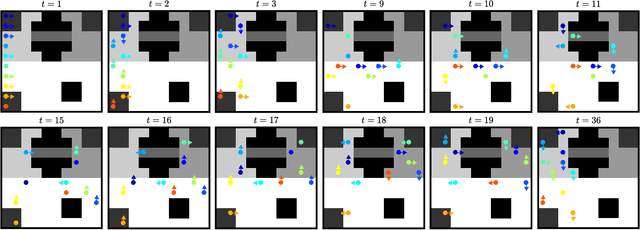
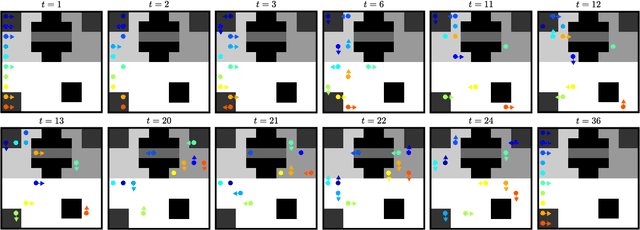
In many multirobot applications, planning trajectories in a way to guarantee that the collective behavior of the robots satisfies a certain high-level specification is crucial. Motivated by this problem, we introduce counting temporal logics---formal languages that enable concise expression of multirobot task specifications over possibly infinite horizons. We first introduce a general logic called counting linear temporal logic plus (cLTL+), and propose an optimization-based method that generates individual trajectories such that satisfaction of a given cLTL+ formula is guaranteed when these trajectories are synchronously executed. We then introduce a fragment of cLTL+, called counting linear temporal logic (cLTL), and show that a solution to planning problem with cLTL constraints can be obtained more efficiently if all robots have identical dynamics. In the second part of the paper, we relax the synchrony assumption and discuss how to generate trajectories that can be asynchronously executed, while preserving the satisfaction of the desired cLTL+ specification. In particular, we show that when the asynchrony between robots is bounded, the method presented in this paper can be modified to generate robust trajectories. We demonstrate these ideas with an experiment and provide numerical results that showcase the scalability of the method.