Privacy protection under the exposure of systems' prior information

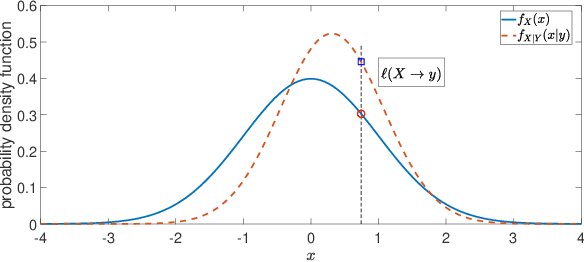
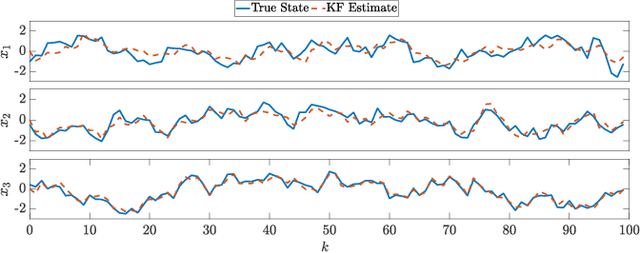
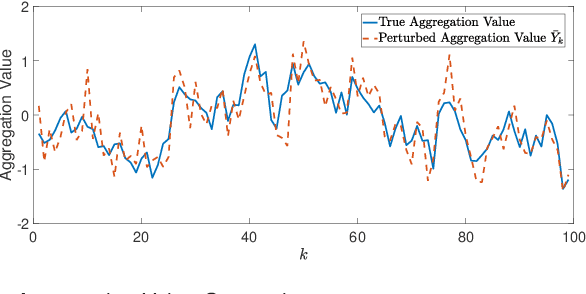
For systems whose states implicate sensitive information, their privacy is of great concern. While notions like differential privacy have been successfully introduced to dynamical systems, it is still unclear how a system's privacy can be properly protected when facing the challenging yet frequently-encountered scenario where an adversary possesses prior knowledge, e.g., the steady state, of the system. This paper presents a new systematic approach to protect the privacy of a discrete-time linear time-invariant system against adversaries knowledgeable of the system's prior information. We employ a tailored \emph{pointwise maximal leakage (PML) privacy} criterion. PML characterizes the worst-case privacy performance, which is sharply different from that of the better-known mutual-information privacy. We derive necessary and sufficient conditions for PML privacy and construct tractable design procedures. Furthermore, our analysis leads to insight into how PML privacy, differential privacy, and mutual-information privacy are related. We then revisit Kalman filters from the perspective of PML privacy and derive a lower bound on the steady-state estimation-error covariance in terms of the PML parameters. Finally, the derived results are illustrated in a case study of privacy protection for distributed sensing in smart buildings.

Learning Stabilizable Deep Dynamics Models

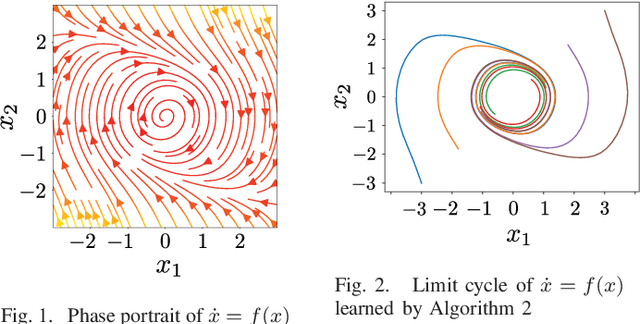
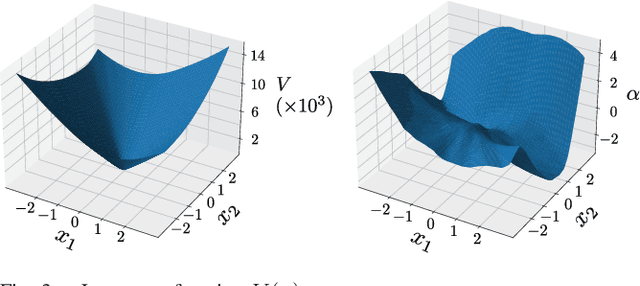
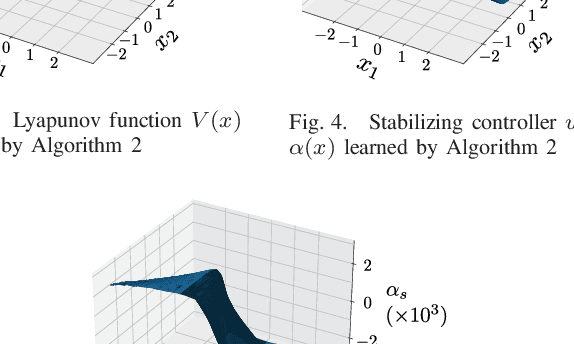
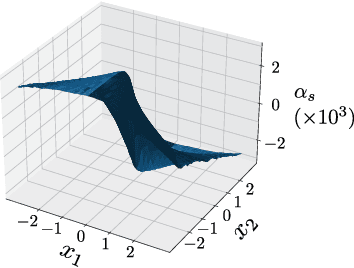
When neural networks are used to model dynamics, properties such as stability of the dynamics are generally not guaranteed. In contrast, there is a recent method for learning the dynamics of autonomous systems that guarantees global exponential stability using neural networks. In this paper, we propose a new method for learning the dynamics of input-affine control systems. An important feature is that a stabilizing controller and control Lyapunov function of the learned model are obtained as well. Moreover, the proposed method can also be applied to solving Hamilton-Jacobi inequalities. The usefulness of the proposed method is examined through numerical examples.