Data-driven Nonlinear Modal Analysis with Physics-constrained Deep Learning: Numerical and Experimental Study

To fully understand, analyze, and determine the behavior of dynamical systems, it is crucial to identify their intrinsic modal coordinates. In nonlinear dynamical systems, this task is challenging as the modal transformation based on the superposition principle that works well for linear systems is no longer applicable. To understand the nonlinear dynamics of a system, one of the main approaches is to use the framework of Nonlinear Normal Modes (NNMs) which attempts to provide an in-depth representation. In this research, we examine the effectiveness of NNMs in characterizing nonlinear dynamical systems. Given the difficulty of obtaining closed-form models or equations for these real-world systems, we present a data-driven framework that combines physics and deep learning to the nonlinear modal transformation function of NNMs from response data only. We assess the framework's ability to represent the system by analyzing its mode decomposition, reconstruction, and prediction accuracy using a nonlinear beam as an example. Initially, we perform numerical simulations on a nonlinear beam at different energy levels in both linear and nonlinear scenarios. Afterward, using experimental vibration data of a nonlinear beam, we isolate the first two NNMs. It is observed that the NNMs' frequency values increase as the excitation level of energy increases, and the configuration plots become more twisted (more nonlinear). In the experiment, the framework successfully decomposed the first two NNMs of the nonlinear beam using experimental free vibration data and captured the dynamics of the structure via prediction and reconstruction of some physical points of the beam.

Data-driven identification of nonlinear dynamical systems with LSTM autoencoders and Normalizing Flows

While linear systems have been useful in solving problems across different fields, the need for improved performance and efficiency has prompted them to operate in nonlinear modes. As a result, nonlinear models are now essential for the design and control of these systems. However, identifying a nonlinear system is more complicated than identifying a linear one. Therefore, modeling and identifying nonlinear systems are crucial for the design, manufacturing, and testing of complex systems. This study presents using advanced nonlinear methods based on deep learning for system identification. Two deep neural network models, LSTM autoencoder and Normalizing Flows, are explored for their potential to extract temporal features from time series data and relate them to system parameters, respectively. The presented framework offers a nonlinear approach to system identification, enabling it to handle complex systems. As case studies, we consider Duffing and Lorenz systems, as well as fluid flows such as flows over a cylinder and the 2-D lid-driven cavity problem. The results indicate that the presented framework is capable of capturing features and effectively relating them to system parameters, satisfying the identification requirements of nonlinear systems.

Data-driven Modeling of Parameterized Nonlinear Fluid Dynamical Systems with a Dynamics-embedded Conditional Generative Adversarial Network

This work presents a data-driven solution to accurately predict parameterized nonlinear fluid dynamical systems using a dynamics-generator conditional GAN (Dyn-cGAN) as a surrogate model. The Dyn-cGAN includes a dynamics block within a modified conditional GAN, enabling the simultaneous identification of temporal dynamics and their dependence on system parameters. The learned Dyn-cGAN model takes into account the system parameters to predict the flow fields of the system accurately. We evaluate the effectiveness and limitations of the developed Dyn-cGAN through numerical studies of various parameterized nonlinear fluid dynamical systems, including flow over a cylinder and a 2-D cavity problem, with different Reynolds numbers. Furthermore, we examine how Reynolds number affects the accuracy of the predictions for both case studies. Additionally, we investigate the impact of the number of time steps involved in the process of dynamics block training on the accuracy of predictions, and we find that an optimal value exists based on errors and mutual information relative to the ground truth.

Extracting full-field subpixel structural displacements from videos via deep learning

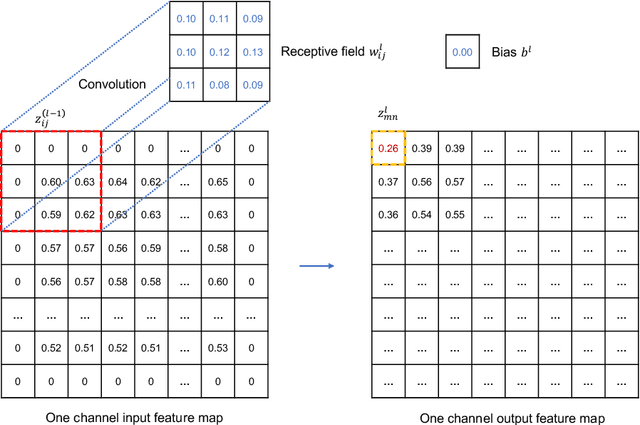
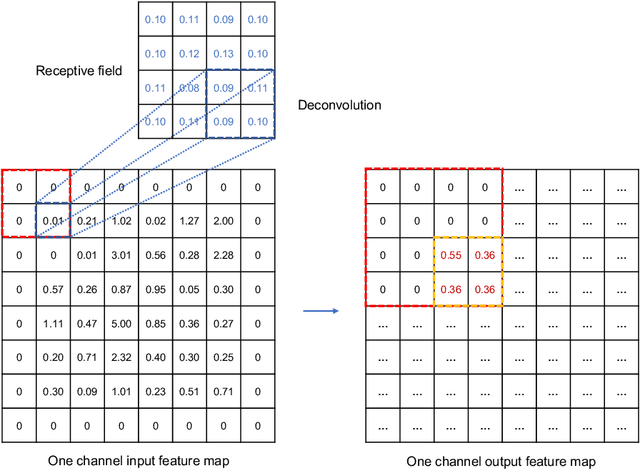
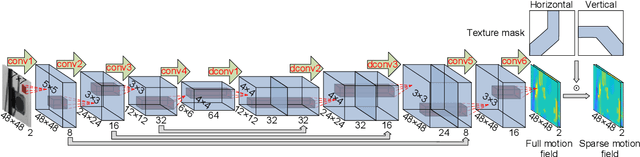
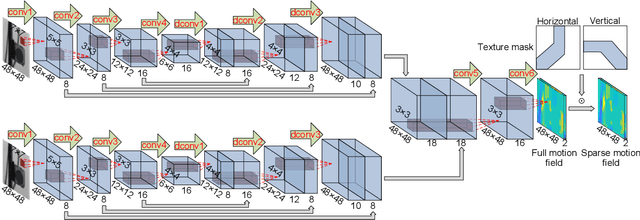
This paper develops a deep learning framework based on convolutional neural networks (CNNs) that enable real-time extraction of full-field subpixel structural displacements from videos. In particular, two new CNN architectures are designed and trained on a dataset generated by the phase-based motion extraction method from a single lab-recorded high-speed video of a dynamic structure. As displacement is only reliable in the regions with sufficient texture contrast, the sparsity of motion field induced by the texture mask is considered via the network architecture design and loss function definition. Results show that, with the supervision of full and sparse motion field, the trained network is capable of identifying the pixels with sufficient texture contrast as well as their subpixel motions. The performance of the trained networks is tested on various videos of other structures to extract the full-field motion (e.g., displacement time histories), which indicates that the trained networks have generalizability to accurately extract full-field subtle displacements for pixels with sufficient texture contrast.