PBCounter: Weighted Model Counting on Pseudo-Boolean Formulas

In Weighted Model Counting (WMC), we assign weights to literals and compute the sum of the weights of the models of a given propositional formula where the weight of an assignment is the product of the weights of its literals. The current WMC solvers work on Conjunctive Normal Form (CNF) formulas. However, CNF is not a natural representation for human-being in many applications. Motivated by the stronger expressive power of pseudo-Boolean (PB) formulas than CNF, we propose to perform WMC on PB formulas. Based on a recent dynamic programming algorithm framework called ADDMC for WMC, we implement a weighted PB counting tool PBCounter. We compare PBCounter with the state-of-the-art weighted model counters SharpSAT-TD, ExactMC, D4, and ADDMC, where the latter tools work on CNF with encoding methods that convert PB constraints into a CNF formula. The experiments on three domains of benchmarks show that PBCounter is superior to the model counters on CNF formulas.

Variants of Tagged Sentential Decision Diagrams

A recently proposed canonical form of Boolean functions, namely tagged sentential decision diagrams (TSDDs), exploits both the standard and zero-suppressed trimming rules. The standard ones minimize the size of sentential decision diagrams (SDDs) while the zero-suppressed trimming rules have the same objective as the standard ones but for zero-suppressed sentential decision diagrams (ZSDDs). The original TSDDs, which we call zero-suppressed TSDDs (ZTSDDs), firstly fully utilize the zero-suppressed trimming rules, and then the standard ones. In this paper, we present a variant of TSDDs which we call standard TSDDs (STSDDs) by reversing the order of trimming rules. We then prove the canonicity of STSDDs and present the algorithms for binary operations on TSDDs. In addition, we offer two kinds of implementations of STSDDs and ZTSDDs and acquire three variations of the original TSDDs. Experimental evaluations demonstrate that the four versions of TSDDs have the size advantage over SDDs and ZSDDs.

Fast Converging Anytime Model Counting

Model counting is a fundamental problem which has been influential in many applications, from artificial intelligence to formal verification. Due to the intrinsic hardness of model counting, approximate techniques have been developed to solve real-world instances of model counting. This paper designs a new anytime approach called PartialKC for approximate model counting. The idea is a form of partial knowledge compilation to provide an unbiased estimate of the model count which can converge to the exact count. Our empirical analysis demonstrates that PartialKC achieves significant scalability and accuracy over prior state-of-the-art approximate counters, including satss and STS. Interestingly, the empirical results show that PartialKC reaches convergence for many instances and therefore provides exact model counting performance comparable to state-of-the-art exact counters.

CCDD: A Tractable Representation for Model Counting and Uniform Sampling

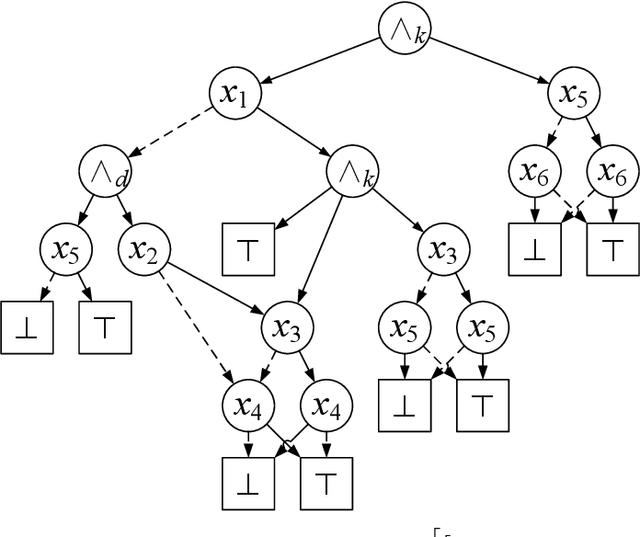
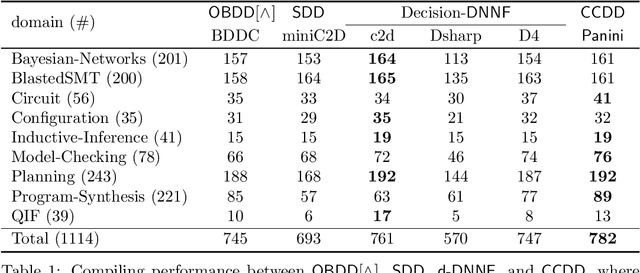
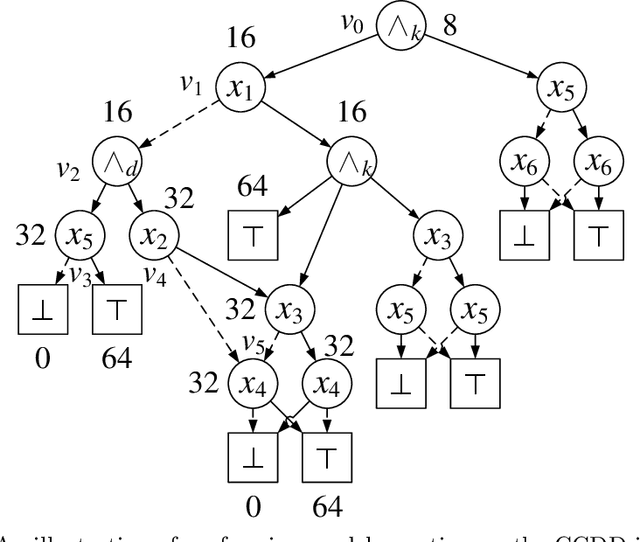
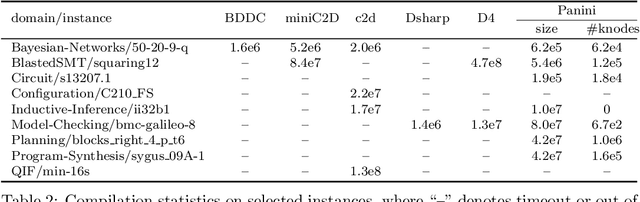
Knowledge compilation concerns with the compilation of representation languages to target languages supporting a wide range of tractable operations arising from diverse areas of computer science. Tractable target compilation languages are usually achieved by restrictions on the internal nodes of the NNF. In this paper, we propose a new representation language CCDD, which introduces new restrictions on conjunction nodes to capture equivalent literals. We show that CCDD supports two key queries, model counting and uniform samping, in polytime. We present algorithms and a compiler to compile propositional formulas expressed in CNF into CCDD. Experiments over a large set of benchmarks show that our compilation times are better with smaller representation than state-of-art Decision-DNNF, SDD and OBDD[AND] compilers. We apply our techniques to model counting and uniform sampling, and develop model counter and uniform sampler on CNF. Our empirical evaluation demonstrates the following significant improvements: our model counter can solve 885 instances while the prior state of the art solved only 843 instances, representing an improvement of 43 instances; and our uniform sampler can solve 780 instances while the prior state of the art solved only 648 instances, representing an improvement of 132 instances.

Approximate Model Counting by Partial Knowledge Compilation

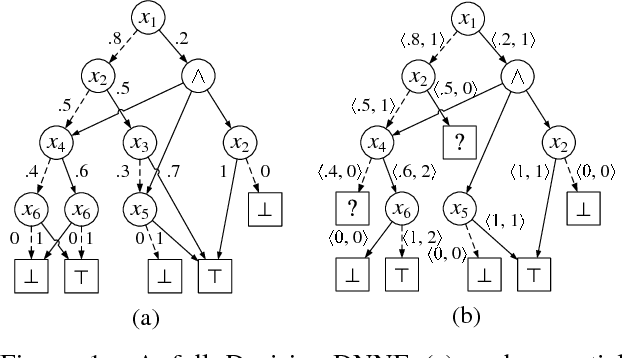
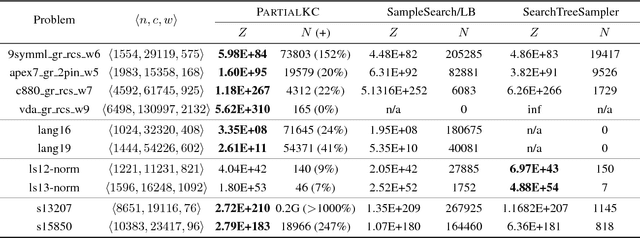
Model counting is the problem of computing the number of satisfying assignments of a given propositional formula. Although exact model counters can be naturally furnished by most of the knowledge compilation (KC) methods, in practice, they fail to generate the compiled results for the exact counting of models for certain formulas due to the explosion in sizes. Decision-DNNF is an important KC language that captures most of the practical compilers. We propose a generalized Decision-DNNF (referred to as partial Decision-DNNF) via introducing a class of new leaf vertices (called unknown vertices), and then propose an algorithm called PartialKC to generate randomly partial Decision-DNNF formulas from the given formulas. An unbiased estimate of the model number can be computed via a randomly partial Decision-DNNF formula. Each calling of PartialKC consists of multiple callings of MicroKC, while each of the latter callings is a process of importance sampling equipped with KC technologies. The experimental results show that PartialKC is more accurate than both SampleSearch and SearchTreeSampler, PartialKC scales better than SearchTreeSampler, and the KC technologies can obviously accelerate sampling.

Ordered {AND, OR}-Decomposition and Binary-Decision Diagram

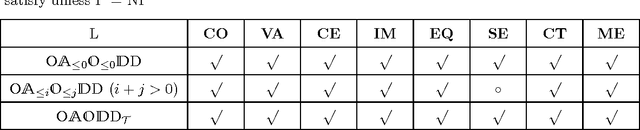
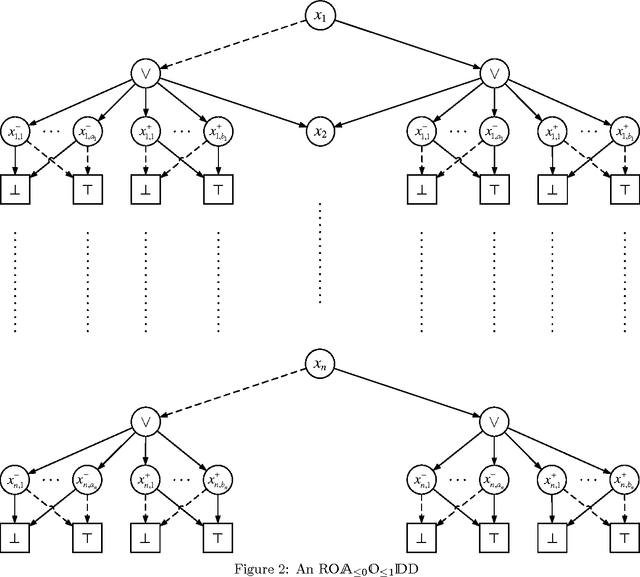
In the context of knowledge compilation (KC), we study the effect of augmenting Ordered Binary Decision Diagrams (OBDD) with two kinds of decomposition nodes, i.e., AND-vertices and OR-vertices which denote conjunctive and disjunctive decomposition of propositional knowledge bases, respectively. The resulting knowledge compilation language is called Ordered {AND, OR}-decomposition and binary-Decision Diagram (OAODD). Roughly speaking, several previous languages can be seen as special types of OAODD, including OBDD, AND/OR Binary Decision Diagram (AOBDD), OBDD with implied Literals (OBDD-L), Multi-Level Decomposition Diagrams (MLDD). On the one hand, we propose some families of algorithms which can convert some fragments of OAODD into others; on the other hand, we present a rich set of polynomial-time algorithms that perform logical operations. According to these algorithms, as well as theoretical analysis, we characterize the space efficiency and tractability of OAODD and its some fragments with respect to the evaluating criteria in the KC map. Finally, we present a compilation algorithm which can convert formulas in negative normal form into OAODD.

Augmenting Ordered Binary Decision Diagrams with Conjunctive Decomposition

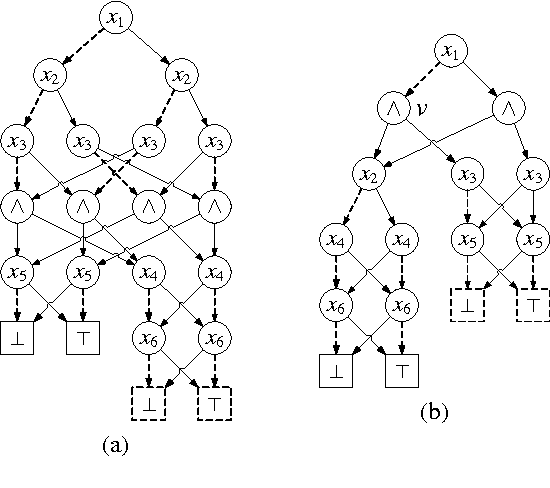
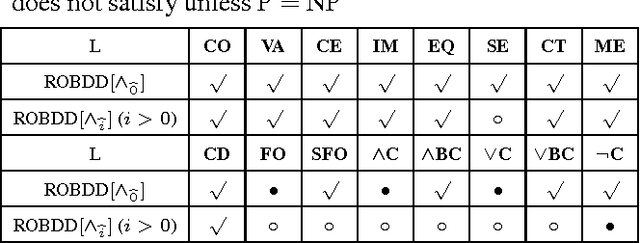
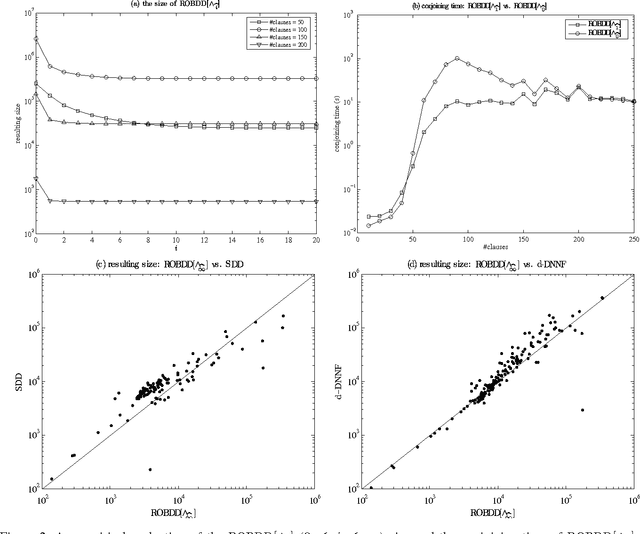
This paper augments OBDD with conjunctive decomposition to propose a generalization called OBDD[$\wedge$]. By imposing reducedness and the finest $\wedge$-decomposition bounded by integer $i$ ($\wedge_{\widehat{i}}$-decomposition) on OBDD[$\wedge$], we identify a family of canonical languages called ROBDD[$\wedge_{\widehat{i}}$], where ROBDD[$\wedge_{\widehat{0}}$] is equivalent to ROBDD. We show that the succinctness of ROBDD[$\wedge_{\widehat{i}}$] is strictly increasing when $i$ increases. We introduce a new time-efficiency criterion called rapidity which reflects that exponential operations may be preferable if the language can be exponentially more succinct, and show that: the rapidity of each operation on ROBDD[$\wedge_{\widehat{i}}$] is increasing when $i$ increases; particularly, the rapidity of some operations (e.g., conjoining) is strictly increasing. Finally, our empirical results show that: a) the size of ROBDD[$\wedge_{\widehat{i}}$] is normally not larger than that of the equivalent \ROBDDC{\widehat{i+1}}; b) conjoining two ROBDD[$\wedge_{\widehat{1}}$]s is more efficient than conjoining two ROBDD[$\wedge_{\widehat{0}}$]s in most cases, where the former is NP-hard but the latter is in P; and c) the space-efficiency of ROBDD[$\wedge_{\widehat{\infty}}$] is comparable with that of d-DNNF and that of another canonical generalization of \ROBDD{} called SDD.

Reduced Ordered Binary Decision Diagram with Implied Literals: A New knowledge Compilation Approach

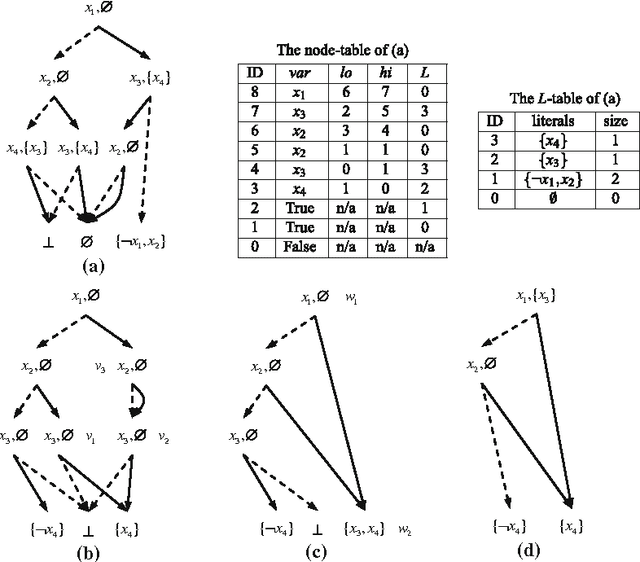
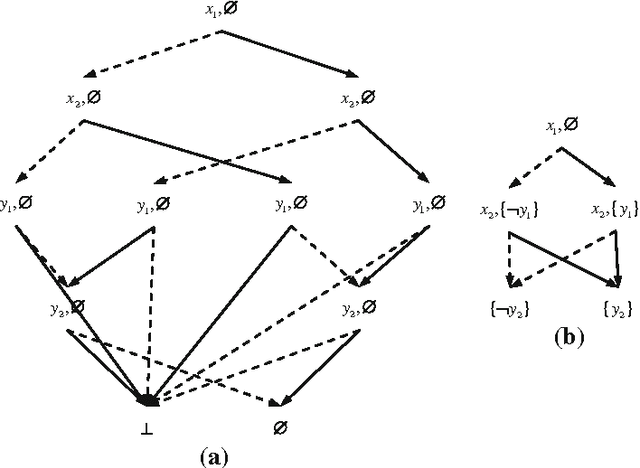
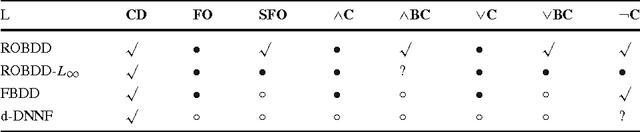
Knowledge compilation is an approach to tackle the computational intractability of general reasoning problems. According to this approach, knowledge bases are converted off-line into a target compilation language which is tractable for on-line querying. Reduced ordered binary decision diagram (ROBDD) is one of the most influential target languages. We generalize ROBDD by associating some implied literals in each node and the new language is called reduced ordered binary decision diagram with implied literals (ROBDD-L). Then we discuss a kind of subsets of ROBDD-L called ROBDD-i with precisely i implied literals (0 \leq i \leq \infty). In particular, ROBDD-0 is isomorphic to ROBDD; ROBDD-\infty requires that each node should be associated by the implied literals as many as possible. We show that ROBDD-i has uniqueness over some specific variables order, and ROBDD-\infty is the most succinct subset in ROBDD-L and can meet most of the querying requirements involved in the knowledge compilation map. Finally, we propose an ROBDD-i compilation algorithm for any i and a ROBDD-\infty compilation algorithm. Based on them, we implement a ROBDD-L package called BDDjLu and then get some conclusions from preliminary experimental results: ROBDD-\infty is obviously smaller than ROBDD for all benchmarks; ROBDD-\infty is smaller than the d-DNNF the benchmarks whose compilation results are relatively small; it seems that it is better to transform ROBDDs-\infty into FBDDs and ROBDDs rather than straight compile the benchmarks.