Accurate Tracking of Arabidopsis Root Cortex Cell Nuclei in 3D Time-Lapse Microscopy Images Based on Genetic Algorithm

Arabidopsis is a widely used model plant to gain basic knowledge on plant physiology and development. Live imaging is an important technique to visualize and quantify elemental processes in plant development. To uncover novel theories underlying plant growth and cell division, accurate cell tracking on live imaging is of utmost importance. The commonly used cell tracking software, TrackMate, adopts tracking-by-detection fashion, which applies Laplacian of Gaussian (LoG) for blob detection, and Linear Assignment Problem (LAP) tracker for tracking. However, they do not perform sufficiently when cells are densely arranged. To alleviate the problems mentioned above, we propose an accurate tracking method based on Genetic algorithm (GA) using knowledge of Arabidopsis root cellular patterns and spatial relationship among volumes. Our method can be described as a coarse-to-fine method, in which we first conducted relatively easy line-level tracking of cell nuclei, then performed complicated nuclear tracking based on known linear arrangement of cell files and their spatial relationship between nuclei. Our method has been evaluated on a long-time live imaging dataset of Arabidopsis root tips, and with minor manual rectification, it accurately tracks nuclei. To the best of our knowledge, this research represents the first successful attempt to address a long-standing problem in the field of time-lapse microscopy in the root meristem by proposing an accurate tracking method for Arabidopsis root nuclei.

Bayesian Masking: Sparse Bayesian Estimation with Weaker Shrinkage Bias

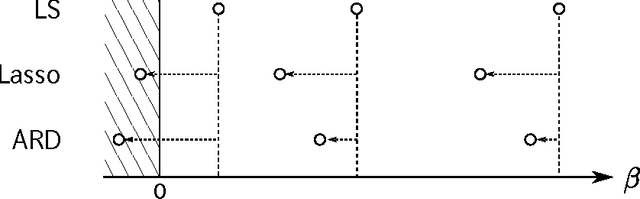
A common strategy for sparse linear regression is to introduce regularization, which eliminates irrelevant features by letting the corresponding weights be zeros. However, regularization often shrinks the estimator for relevant features, which leads to incorrect feature selection. Motivated by the above-mentioned issue, we propose Bayesian masking (BM), a sparse estimation method which imposes no regularization on the weights. The key concept of BM is to introduce binary latent variables that randomly mask features. Estimating the masking rates determines the relevance of the features automatically. We derive a variational Bayesian inference algorithm that maximizes the lower bound of the factorized information criterion (FIC), which is a recently developed asymptotic criterion for evaluating the marginal log-likelihood. In addition, we propose reparametrization to accelerate the convergence of the derived algorithm. Finally, we show that BM outperforms Lasso and automatic relevance determination (ARD) in terms of the sparsity-shrinkage trade-off.