Subquadratic Algorithms and Hardness for Attention with Any Temperature

Despite the popularity of the Transformer architecture, the standard algorithm for computing Attention suffers from quadratic time complexity in context length $n$. Alman and Song [NeurIPS 2023] showed that when the head dimension $d = \Theta(\log n)$, subquadratic Attention is possible if and only if the inputs have small entries bounded by $B = o(\sqrt{\log n})$ in absolute values, under the Strong Exponential Time Hypothesis ($\mathsf{SETH}$). Equivalently, subquadratic Attention is possible if and only if the softmax is applied with high temperature for $d=\Theta(\log n)$. Running times of these algorithms depend exponentially on $B$ and thus they do not lead to even a polynomial-time algorithm outside the specific range of $B$. This naturally leads to the question: when can Attention be computed efficiently without strong assumptions on temperature? Are there fast attention algorithms that scale polylogarithmically with entry size $B$? In this work, we resolve this question and characterize when fast Attention for arbitrary temperatures is possible. First, for all constant $d = O(1)$, we give the first subquadratic $\tilde{O}(n^{2 - 1/d} \cdot \mathrm{polylog}(B))$ time algorithm for Attention with large $B$. Our result holds even for matrices with large head dimension if they have low rank. In this regime, we also give a similar running time for Attention gradient computation, and therefore for the full LLM training process. Furthermore, we show that any substantial improvement on our algorithm is unlikely. In particular, we show that even when $d = 2^{\Theta(\log^* n)}$, Attention requires $n^{2 - o(1)}$ time under $\mathsf{SETH}$. Finally, in the regime where $d = \mathrm{poly}(n)$, we show that the standard algorithm is optimal under popular fine-grained complexity assumptions.

Fine-Grained Complexity and Algorithms for the Schulze Voting Method

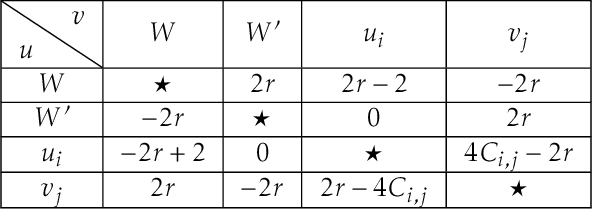
We study computational aspects of a well-known single-winner voting rule called the Schulze method [Schulze, 2003] which is used broadly in practice. In this method the voters give (weak) ordinal preference ballots which are used to define the weighted majority graph (WMG) of direct comparisons between pairs of candidates. The choice of the winner comes from indirect comparisons in the graph, and more specifically from considering directed paths instead of direct comparisons between candidates. When the input is the WMG, to our knowledge, the fastest algorithm for computing all possible winners in the Schulze method uses a folklore reduction to the All-Pairs Bottleneck Paths (APBP) problem and runs in $O(m^{2.69})$ time, where $m$ is the number of candidates. It is an interesting open question whether this can be improved. Our first result is a combinatorial algorithm with a nearly quadratic running time for computing all possible winners. If the input to the possible winners problem is not the WMG but the preference profile, then constructing the WMG is a bottleneck that increases the running time significantly; in the special case when there are $O(m)$ voters and candidates, the running time becomes $O(m^{2.69})$, or $O(m^{2.5})$ if there is a nearly-linear time algorithm for multiplying dense square matrices. To address this bottleneck, we prove a formal equivalence between the well-studied Dominance Product problem and the problem of computing the WMG. We prove a similar connection between the so called Dominating Pairs problem and the problem of verifying whether a given candidate is a possible winner. Our paper is the first to bring fine-grained complexity into the field of computational social choice. Using it we can identify voting protocols that are unlikely to be practical for large numbers of candidates and/or voters, as their complexity is likely, say at least cubic.

HappyDB: A Corpus of 100,000 Crowdsourced Happy Moments

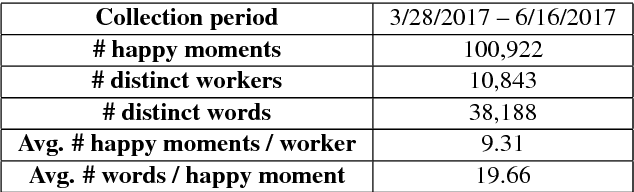
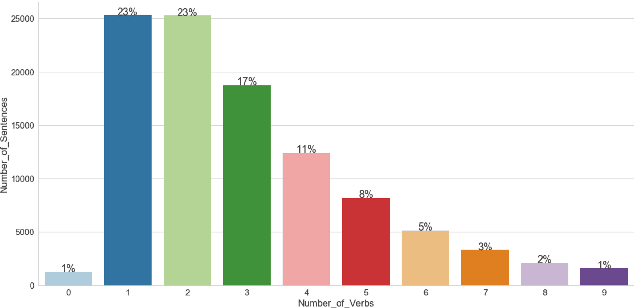
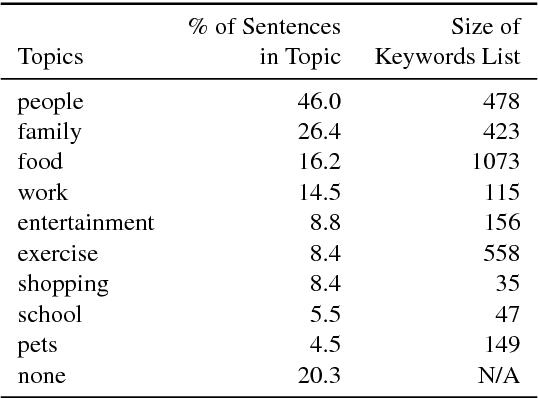
The science of happiness is an area of positive psychology concerned with understanding what behaviors make people happy in a sustainable fashion. Recently, there has been interest in developing technologies that help incorporate the findings of the science of happiness into users' daily lives by steering them towards behaviors that increase happiness. With the goal of building technology that can understand how people express their happy moments in text, we crowd-sourced HappyDB, a corpus of 100,000 happy moments that we make publicly available. This paper describes HappyDB and its properties, and outlines several important NLP problems that can be studied with the help of the corpus. We also apply several state-of-the-art analysis techniques to analyze HappyDB. Our results demonstrate the need for deeper NLP techniques to be developed which makes HappyDB an exciting resource for follow-on research.