DVI: Disentangling Semantic and Visual Identity for Training-Free Personalized Generation

Recent tuning-free identity customization methods achieve high facial fidelity but often overlook visual context, such as lighting, skin texture, and environmental tone. This limitation leads to ``Semantic-Visual Dissonance,'' where accurate facial geometry clashes with the input's unique atmosphere, causing an unnatural ``sticker-like'' effect. We propose **DVI (Disentangled Visual-Identity)**, a zero-shot framework that orthogonally disentangles identity into fine-grained semantic and coarse-grained visual streams. Unlike methods relying solely on semantic vectors, DVI exploits the inherent statistical properties of the VAE latent space, utilizing mean and variance as lightweight descriptors for global visual atmosphere. We introduce a **Parameter-Free Feature Modulation** mechanism that adaptively modulates semantic embeddings with these visual statistics, effectively injecting the reference's ``visual soul'' without training. Furthermore, a **Dynamic Temporal Granularity Scheduler** aligns with the diffusion process, prioritizing visual atmosphere in early denoising stages while refining semantic details later. Extensive experiments demonstrate that DVI significantly enhances visual consistency and atmospheric fidelity without parameter fine-tuning, maintaining robust identity preservation and outperforming state-of-the-art methods in IBench evaluations.

Bounds on mutual information of mixture data for classification tasks

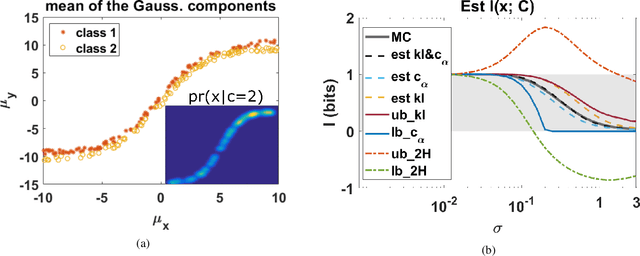
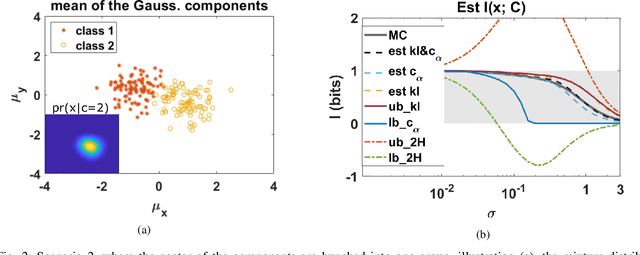
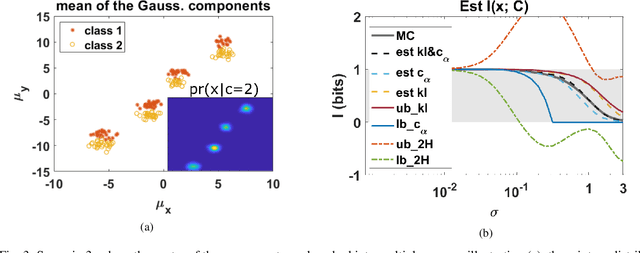
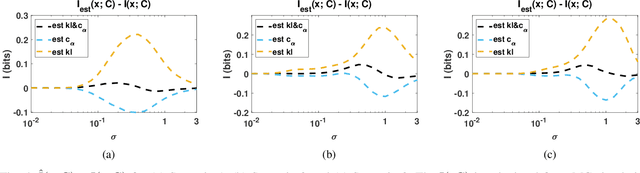
The data for many classification problems, such as pattern and speech recognition, follow mixture distributions. To quantify the optimum performance for classification tasks, the Shannon mutual information is a natural information-theoretic metric, as it is directly related to the probability of error. The mutual information between mixture data and the class label does not have an analytical expression, nor any efficient computational algorithms. We introduce a variational upper bound, a lower bound, and three estimators, all employing pair-wise divergences between mixture components. We compare the new bounds and estimators with Monte Carlo stochastic sampling and bounds derived from entropy bounds. To conclude, we evaluate the performance of the bounds and estimators through numerical simulations.