Graph Wave Networks

Dynamics modeling has been introduced as a novel paradigm in message passing (MP) of graph neural networks (GNNs). Existing methods consider MP between nodes as a heat diffusion process, and leverage heat equation to model the temporal evolution of nodes in the embedding space. However, heat equation can hardly depict the wave nature of graph signals in graph signal processing. Besides, heat equation is essentially a partial differential equation (PDE) involving a first partial derivative of time, whose numerical solution usually has low stability, and leads to inefficient model training. In this paper, we would like to depict more wave details in MP, since graph signals are essentially wave signals that can be seen as a superposition of a series of waves in the form of eigenvector. This motivates us to consider MP as a wave propagation process to capture the temporal evolution of wave signals in the space. Based on wave equation in physics, we innovatively develop a graph wave equation to leverage the wave propagation on graphs. In details, we demonstrate that the graph wave equation can be connected to traditional spectral GNNs, facilitating the design of graph wave networks based on various Laplacians and enhancing the performance of the spectral GNNs. Besides, the graph wave equation is particularly a PDE involving a second partial derivative of time, which has stronger stability on graphs than the heat equation that involves a first partial derivative of time. Additionally, we theoretically prove that the numerical solution derived from the graph wave equation are constantly stable, enabling to significantly enhance model efficiency while ensuring its performance. Extensive experiments show that GWNs achieve SOTA and efficient performance on benchmark datasets, and exhibit outstanding performance in addressing challenging graph problems, such as over-smoothing and heterophily.

Homogeneous Feature Transfer and Heterogeneous Location Fine-tuning for Cross-City Property Appraisal Framework

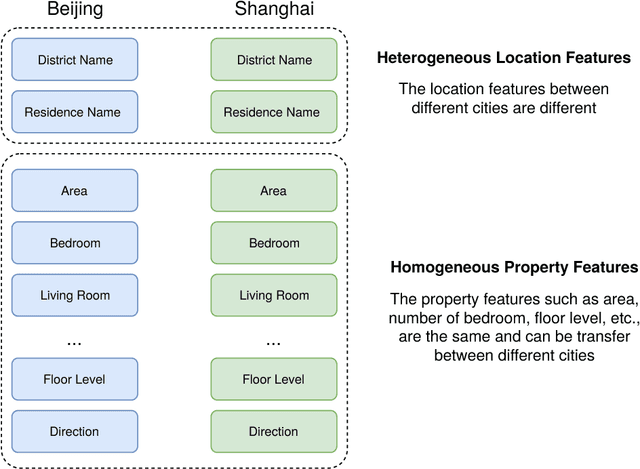
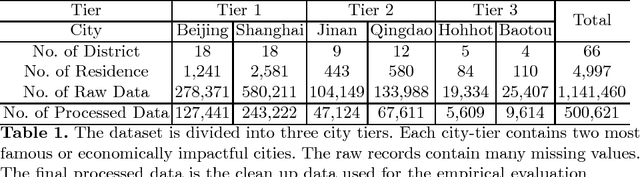
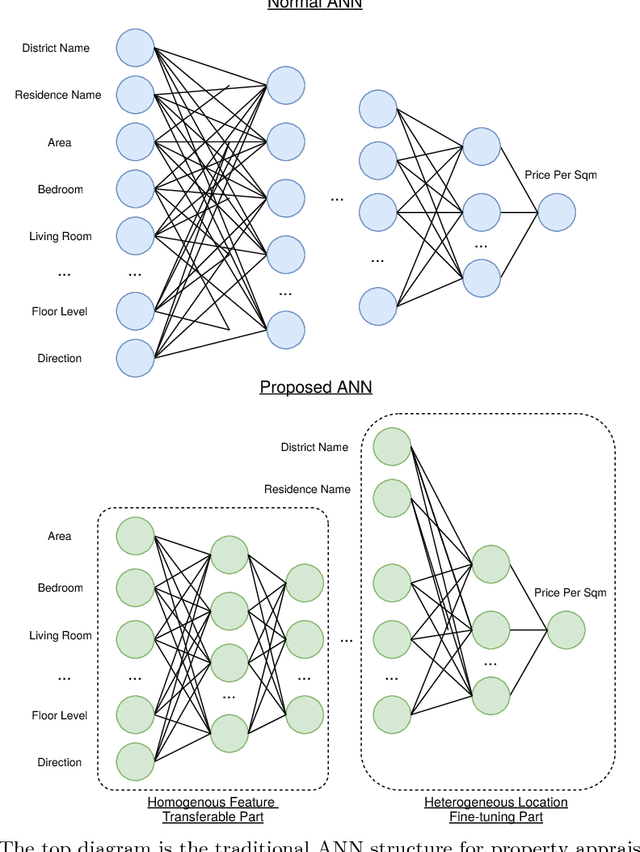
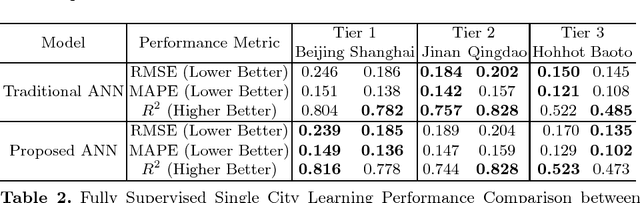
Most existing real estate appraisal methods focus on building accuracy and reliable models from a given dataset but pay little attention to the extensibility of their trained model. As different cities usually contain a different set of location features (district names, apartment names), most existing mass appraisal methods have to train a new model from scratch for different cities or regions. As a result, these approaches require massive data collection for each city and the total training time for a multi-city property appraisal system will be extremely long. Besides, some small cities may not have enough data for training a robust appraisal model. To overcome these limitations, we develop a novel Homogeneous Feature Transfer and Heterogeneous Location Fine-tuning (HFT+HLF) cross-city property appraisal framework. By transferring partial neural network learning from a source city and fine-tuning on the small amount of location information of a target city, our semi-supervised model can achieve similar or even superior performance compared to a fully supervised Artificial neural network (ANN) method.