Hyperbolic-PDE GNN: Spectral Graph Neural Networks in the Perspective of A System of Hyperbolic Partial Differential Equations

Graph neural networks (GNNs) leverage message passing mechanisms to learn the topological features of graph data. Traditional GNNs learns node features in a spatial domain unrelated to the topology, which can hardly ensure topological features. In this paper, we formulates message passing as a system of hyperbolic partial differential equations (hyperbolic PDEs), constituting a dynamical system that explicitly maps node representations into a particular solution space. This solution space is spanned by a set of eigenvectors describing the topological structure of graphs. Within this system, for any moment in time, a node features can be decomposed into a superposition of the basis of eigenvectors. This not only enhances the interpretability of message passing but also enables the explicit extraction of fundamental characteristics about the topological structure. Furthermore, by solving this system of hyperbolic partial differential equations, we establish a connection with spectral graph neural networks (spectral GNNs), serving as a message passing enhancement paradigm for spectral GNNs.We further introduce polynomials to approximate arbitrary filter functions. Extensive experiments demonstrate that the paradigm of hyperbolic PDEs not only exhibits strong flexibility but also significantly enhances the performance of various spectral GNNs across diverse graph tasks.

Graph Wave Networks

Dynamics modeling has been introduced as a novel paradigm in message passing (MP) of graph neural networks (GNNs). Existing methods consider MP between nodes as a heat diffusion process, and leverage heat equation to model the temporal evolution of nodes in the embedding space. However, heat equation can hardly depict the wave nature of graph signals in graph signal processing. Besides, heat equation is essentially a partial differential equation (PDE) involving a first partial derivative of time, whose numerical solution usually has low stability, and leads to inefficient model training. In this paper, we would like to depict more wave details in MP, since graph signals are essentially wave signals that can be seen as a superposition of a series of waves in the form of eigenvector. This motivates us to consider MP as a wave propagation process to capture the temporal evolution of wave signals in the space. Based on wave equation in physics, we innovatively develop a graph wave equation to leverage the wave propagation on graphs. In details, we demonstrate that the graph wave equation can be connected to traditional spectral GNNs, facilitating the design of graph wave networks based on various Laplacians and enhancing the performance of the spectral GNNs. Besides, the graph wave equation is particularly a PDE involving a second partial derivative of time, which has stronger stability on graphs than the heat equation that involves a first partial derivative of time. Additionally, we theoretically prove that the numerical solution derived from the graph wave equation are constantly stable, enabling to significantly enhance model efficiency while ensuring its performance. Extensive experiments show that GWNs achieve SOTA and efficient performance on benchmark datasets, and exhibit outstanding performance in addressing challenging graph problems, such as over-smoothing and heterophily.

Mitigating Modality Bias in Multi-modal Entity Alignment from a Causal Perspective

Multi-Modal Entity Alignment (MMEA) aims to retrieve equivalent entities from different Multi-Modal Knowledge Graphs (MMKGs), a critical information retrieval task. Existing studies have explored various fusion paradigms and consistency constraints to improve the alignment of equivalent entities, while overlooking that the visual modality may not always contribute positively. Empirically, entities with low-similarity images usually generate unsatisfactory performance, highlighting the limitation of overly relying on visual features. We believe the model can be biased toward the visual modality, leading to a shortcut image-matching task. To address this, we propose a counterfactual debiasing framework for MMEA, termed CDMEA, which investigates visual modality bias from a causal perspective. Our approach aims to leverage both visual and graph modalities to enhance MMEA while suppressing the direct causal effect of the visual modality on model predictions. By estimating the Total Effect (TE) of both modalities and excluding the Natural Direct Effect (NDE) of the visual modality, we ensure that the model predicts based on the Total Indirect Effect (TIE), effectively utilizing both modalities and reducing visual modality bias. Extensive experiments on 9 benchmark datasets show that CDMEA outperforms 14 state-of-the-art methods, especially in low-similarity, high-noise, and low-resource data scenarios.

Adaptive Attentional Network for Few-Shot Knowledge Graph Completion

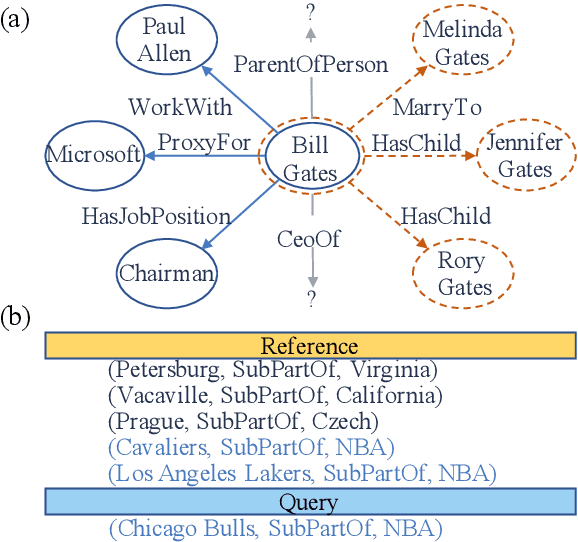
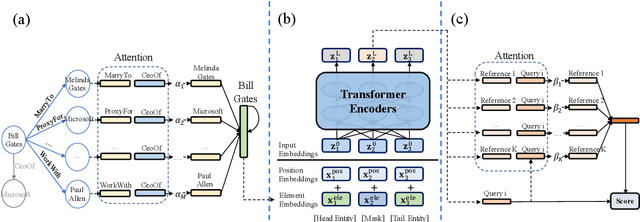
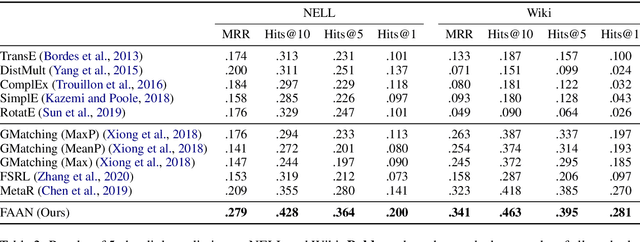
Few-shot Knowledge Graph (KG) completion is a focus of current research, where each task aims at querying unseen facts of a relation given its few-shot reference entity pairs. Recent attempts solve this problem by learning static representations of entities and references, ignoring their dynamic properties, i.e., entities may exhibit diverse roles within task relations, and references may make different contributions to queries. This work proposes an adaptive attentional network for few-shot KG completion by learning adaptive entity and reference representations. Specifically, entities are modeled by an adaptive neighbor encoder to discern their task-oriented roles, while references are modeled by an adaptive query-aware aggregator to differentiate their contributions. Through the attention mechanism, both entities and references can capture their fine-grained semantic meanings, and thus render more expressive representations. This will be more predictive for knowledge acquisition in the few-shot scenario. Evaluation in link prediction on two public datasets shows that our approach achieves new state-of-the-art results with different few-shot sizes.