A Generative Adversarial Network for Climate Tipping Point Discovery (TIP-GAN)

We propose a new Tipping Point Generative Adversarial Network (TIP-GAN) for better characterizing potential climate tipping points in Earth system models. We describe an adversarial game to explore the parameter space of these models, detect upcoming tipping points, and discover the drivers of tipping points. In this setup, a set of generators learn to construct model configurations that will invoke a climate tipping point. The discriminator learns to identify which generators are generating each model configuration and whether a given configuration will lead to a tipping point. The discriminator is trained using an oracle (a surrogate climate model) to test if a generated model configuration leads to a tipping point or not. We demonstrate the application of this GAN to invoke the collapse of the Atlantic Meridional Overturning Circulation (AMOC). We share experimental results of modifying the loss functions and the number of generators to exploit the area of uncertainty in model state space near a climate tipping point. In addition, we show that our trained discriminator can predict AMOC collapse with a high degree of accuracy without the use of the oracle. This approach could generalize to other tipping points, and could augment climate modeling research by directing users interested in studying tipping points to parameter sets likely to induce said tipping points in their computationally intensive climate models.

Using Artificial Intelligence to aid Scientific Discovery of Climate Tipping Points

We propose a hybrid Artificial Intelligence (AI) climate modeling approach that enables climate modelers in scientific discovery using a climate-targeted simulation methodology based on a novel combination of deep neural networks and mathematical methods for modeling dynamical systems. The simulations are grounded by a neuro-symbolic language that both enables question answering of what is learned by the AI methods and provides a means of explainability. We describe how this methodology can be applied to the discovery of climate tipping points and, in particular, the collapse of the Atlantic Meridional Overturning Circulation (AMOC). We show how this methodology is able to predict AMOC collapse with a high degree of accuracy using a surrogate climate model for ocean interaction. We also show preliminary results of neuro-symbolic method performance when translating between natural language questions and symbolically learned representations. Our AI methodology shows promising early results, potentially enabling faster climate tipping point related research that would otherwise be computationally infeasible.

Benchmarking optimality of time series classification methods in distinguishing diffusions

Performance benchmarking is a crucial component of time series classification (TSC) algorithm design, and a fast-growing number of datasets have been established for empirical benchmarking. However, the empirical benchmarks are costly and do not guarantee statistical optimality. This study proposes to benchmark the optimality of TSC algorithms in distinguishing diffusion processes by the likelihood ratio test (LRT). The LRT is optimal in the sense of the Neyman-Pearson lemma: it has the smallest false positive rate among classifiers with a controlled level of false negative rate. The LRT requires the likelihood ratio of the time series to be computable. The diffusion processes from stochastic differential equations provide such time series and are flexible in design for generating linear or nonlinear time series. We demonstrate the benchmarking with three scalable state-of-the-art TSC algorithms: random forest, ResNet, and ROCKET. Test results show that they can achieve LRT optimality for univariate time series and multivariate Gaussian processes. However, these model-agnostic algorithms are suboptimal in classifying nonlinear multivariate time series from high-dimensional stochastic interacting particle systems. Additionally, the LRT benchmark provides tools to analyze the dependence of classification accuracy on the time length, dimension, temporal sampling frequency, and randomness of the time series. Thus, the LRT with diffusion processes can systematically and efficiently benchmark the optimality of TSC algorithms and may guide their future improvements.

Unsupervised learning of observation functions in state-space models by nonparametric moment methods

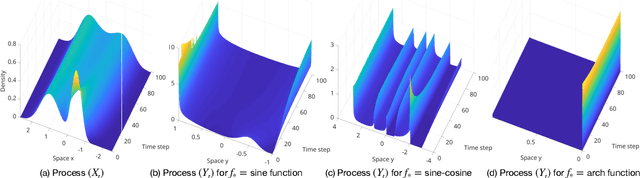
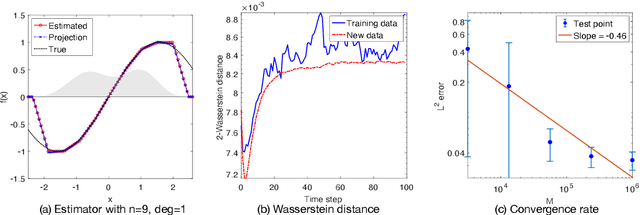
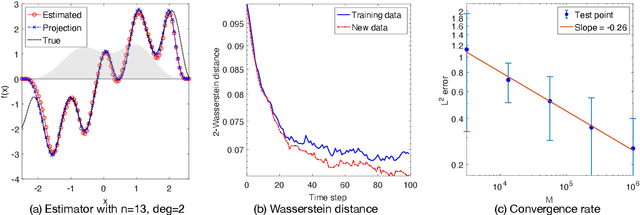
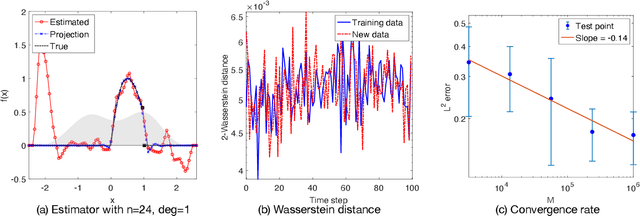
We investigate the unsupervised learning of non-invertible observation functions in nonlinear state-space models. Assuming abundant data of the observation process along with the distribution of the state process, we introduce a nonparametric generalized moment method to estimate the observation function via constrained regression. The major challenge comes from the non-invertibility of the observation function and the lack of data pairs between the state and observation. We address the fundamental issue of identifiability from quadratic loss functionals and show that the function space of identifiability is the closure of a RKHS that is intrinsic to the state process. Numerical results show that the first two moments and temporal correlations, along with upper and lower bounds, can identify functions ranging from piecewise polynomials to smooth functions, leading to convergent estimators. The limitations of this method, such as non-identifiability due to symmetry and stationarity, are also discussed.

Applications of Koopman Mode Analysis to Neural Networks

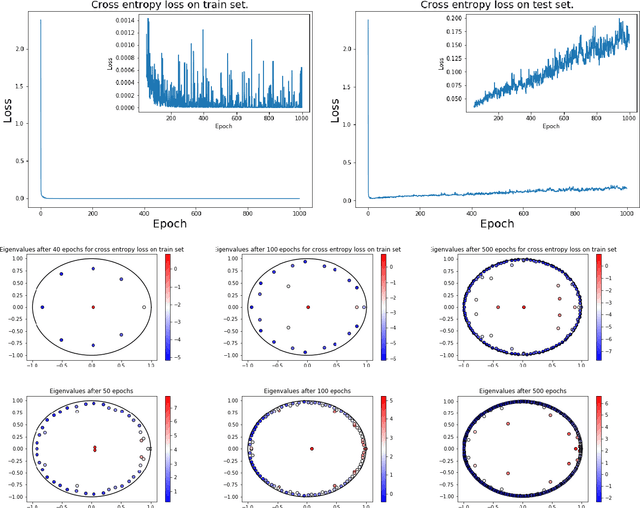
We consider the training process of a neural network as a dynamical system acting on the high-dimensional weight space. Each epoch is an application of the map induced by the optimization algorithm and the loss function. Using this induced map, we can apply observables on the weight space and measure their evolution. The evolution of the observables are given by the Koopman operator associated with the induced dynamical system. We use the spectrum and modes of the Koopman operator to realize the above objectives. Our methods can help to, a priori, determine the network depth; determine if we have a bad initialization of the network weights, allowing a restart before training too long; speeding up the training time. Additionally, our methods help enable noise rejection and improve robustness. We show how the Koopman spectrum can be used to determine the number of layers required for the architecture. Additionally, we show how we can elucidate the convergence versus non-convergence of the training process by monitoring the spectrum, in particular, how the existence of eigenvalues clustering around 1 determines when to terminate the learning process. We also show how using Koopman modes we can selectively prune the network to speed up the training procedure. Finally, we show that incorporating loss functions based on negative Sobolev norms can allow for the reconstruction of a multi-scale signal polluted by very large amounts of noise.