Locality Preserving Projections for Grassmann manifold

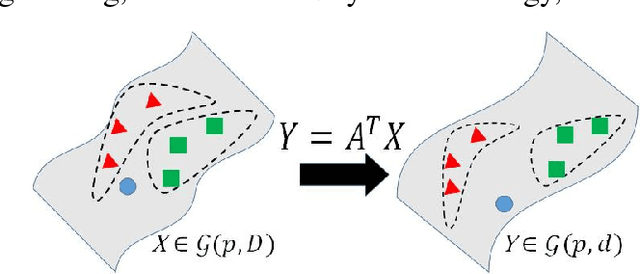
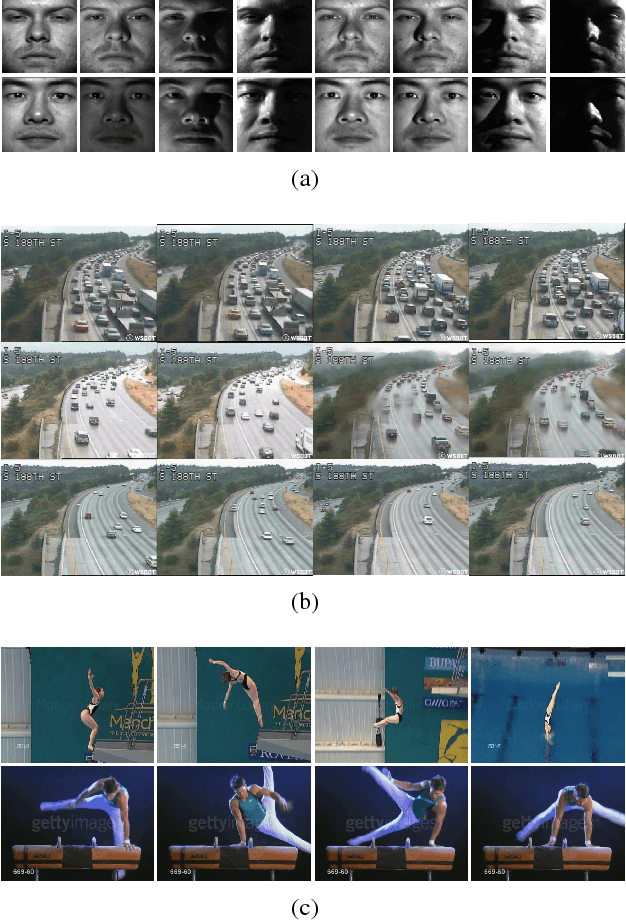
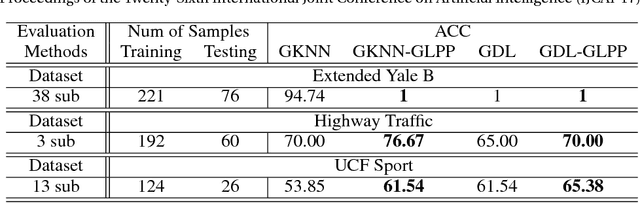
Learning on Grassmann manifold has become popular in many computer vision tasks, with the strong capability to extract discriminative information for imagesets and videos. However, such learning algorithms particularly on high-dimensional Grassmann manifold always involve with significantly high computational cost, which seriously limits the applicability of learning on Grassmann manifold in more wide areas. In this research, we propose an unsupervised dimensionality reduction algorithm on Grassmann manifold based on the Locality Preserving Projections (LPP) criterion. LPP is a commonly used dimensionality reduction algorithm for vector-valued data, aiming to preserve local structure of data in the dimension-reduced space. The strategy is to construct a mapping from higher dimensional Grassmann manifold into the one in a relative low-dimensional with more discriminative capability. The proposed method can be optimized as a basic eigenvalue problem. The performance of our proposed method is assessed on several classification and clustering tasks and the experimental results show its clear advantages over other Grassmann based algorithms.

Block-Diagonal Sparse Representation by Learning a Linear Combination Dictionary for Recognition

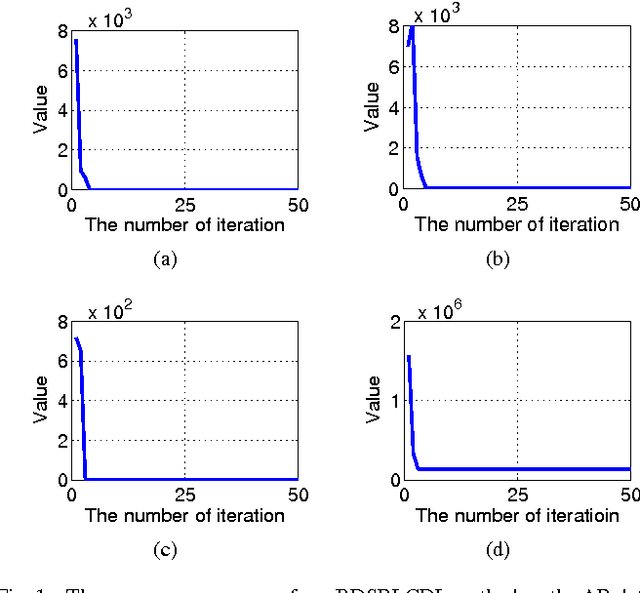
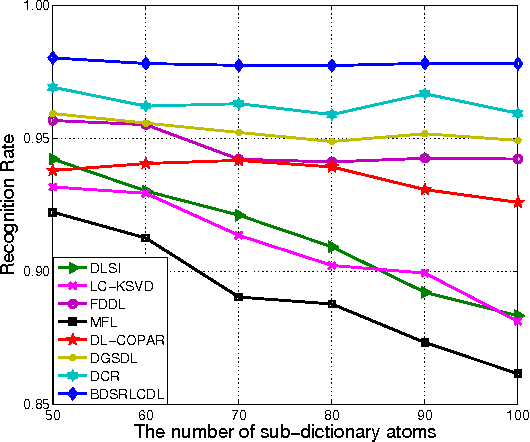
In a sparse representation based recognition scheme, it is critical to learn a desired dictionary, aiming both good representational power and discriminative performance. In this paper, we propose a new dictionary learning model for recognition applications, in which three strategies are adopted to achieve these two objectives simultaneously. First, a block-diagonal constraint is introduced into the model to eliminate the correlation between classes and enhance the discriminative performance. Second, a low-rank term is adopted to model the coherence within classes for refining the sparse representation of each class. Finally, instead of using the conventional over-complete dictionary, a specific dictionary constructed from the linear combination of the training samples is proposed to enhance the representational power of the dictionary and to improve the robustness of the sparse representation model. The proposed method is tested on several public datasets. The experimental results show the method outperforms most state-of-the-art methods.

Tensor Sparse and Low-Rank based Submodule Clustering Method for Multi-way Data

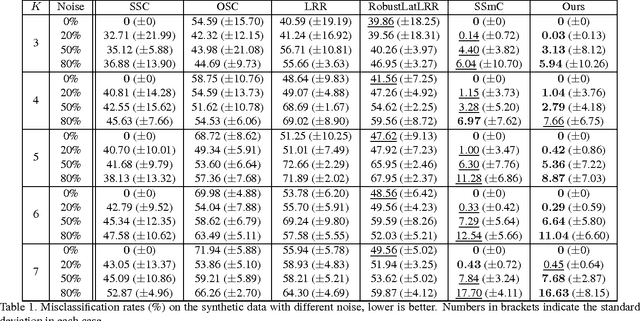
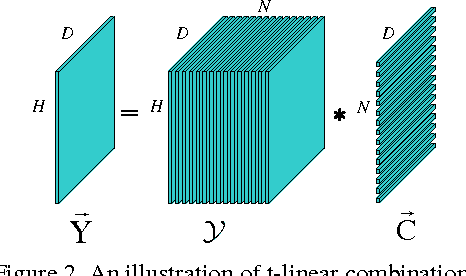
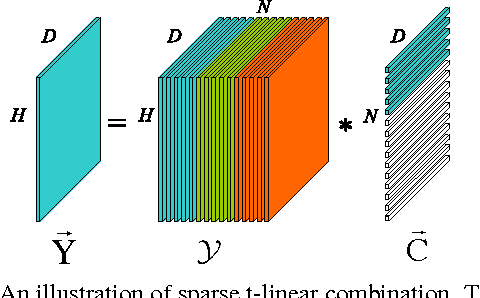
A new submodule clustering method via sparse and low-rank representation for multi-way data is proposed in this paper. Instead of reshaping multi-way data into vectors, this method maintains their natural orders to preserve data intrinsic structures, e.g., image data kept as matrices. To implement clustering, the multi-way data, viewed as tensors, are represented by the proposed tensor sparse and low-rank model to obtain its submodule representation, called a free module, which is finally used for spectral clustering. The proposed method extends the conventional subspace clustering method based on sparse and low-rank representation to multi-way data submodule clustering by combining t-product operator. The new method is tested on several public datasets, including synthetical data, video sequences and toy images. The experiments show that the new method outperforms the state-of-the-art methods, such as Sparse Subspace Clustering (SSC), Low-Rank Representation (LRR), Ordered Subspace Clustering (OSC), Robust Latent Low Rank Representation (RobustLatLRR) and Sparse Submodule Clustering method (SSmC).

Matrix Variate RBM Model with Gaussian Distributions

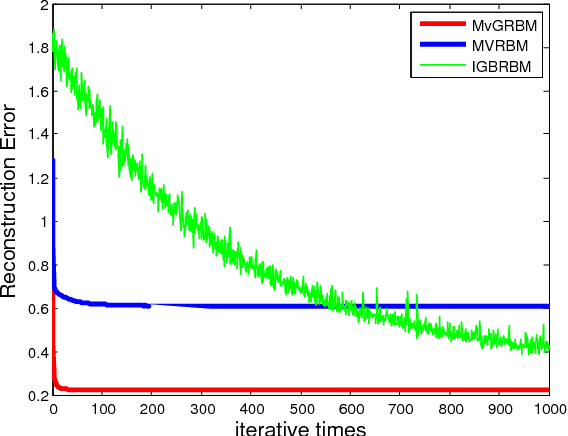
Restricted Boltzmann Machine (RBM) is a particular type of random neural network models modeling vector data based on the assumption of Bernoulli distribution. For multi-dimensional and non-binary data, it is necessary to vectorize and discretize the information in order to apply the conventional RBM. It is well-known that vectorization would destroy internal structure of data, and the binary units will limit the applying performance due to fickle real data. To address the issue, this paper proposes a Matrix variate Gaussian Restricted Boltzmann Machine (MVGRBM) model for matrix data whose entries follow Gaussian distributions. Compared with some other RBM algorithm, MVGRBM can model real value data better and it has good performance in image classification.

Partial Least Squares Regression on Riemannian Manifolds and Its Application in Classifications

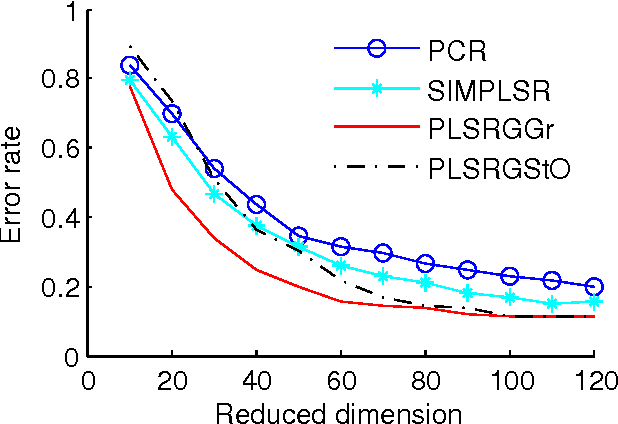
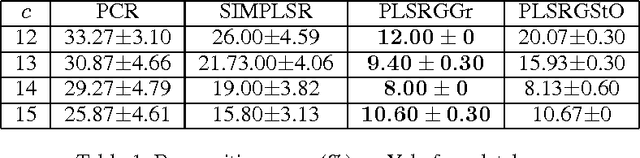
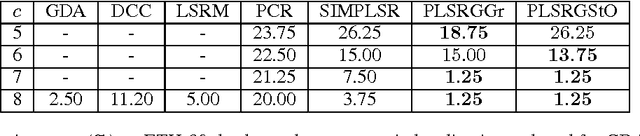
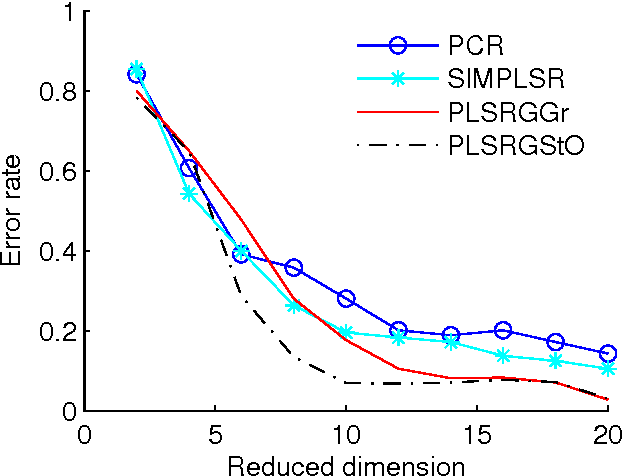
Partial least squares regression (PLSR) has been a popular technique to explore the linear relationship between two datasets. However, most of algorithm implementations of PLSR may only achieve a suboptimal solution through an optimization on the Euclidean space. In this paper, we propose several novel PLSR models on Riemannian manifolds and develop optimization algorithms based on Riemannian geometry of manifolds. This algorithm can calculate all the factors of PLSR globally to avoid suboptimal solutions. In a number of experiments, we have demonstrated the benefits of applying the proposed model and algorithm to a variety of learning tasks in pattern recognition and object classification.

Laplacian LRR on Product Grassmann Manifolds for Human Activity Clustering in Multi-Camera Video Surveillance

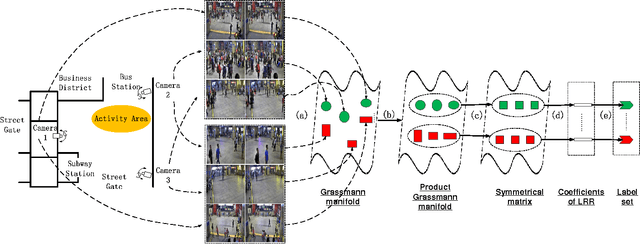
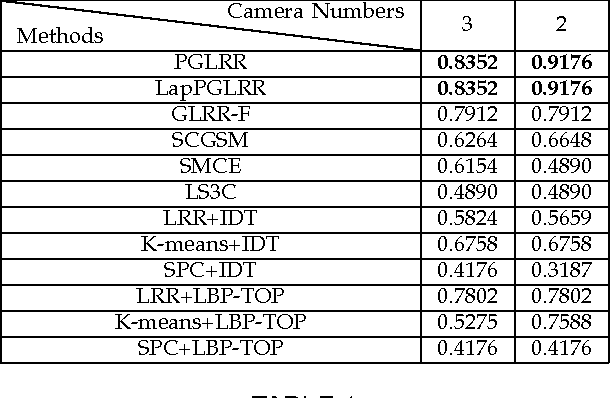
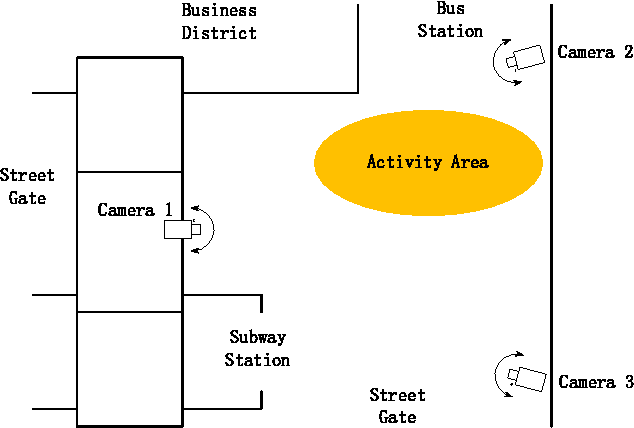
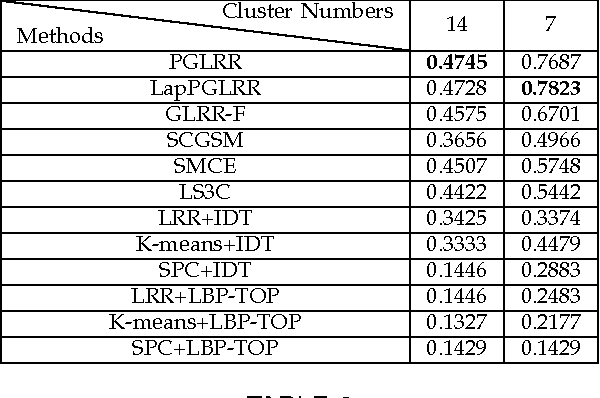
In multi-camera video surveillance, it is challenging to represent videos from different cameras properly and fuse them efficiently for specific applications such as human activity recognition and clustering. In this paper, a novel representation for multi-camera video data, namely the Product Grassmann Manifold (PGM), is proposed to model video sequences as points on the Grassmann manifold and integrate them as a whole in the product manifold form. Additionally, with a new geometry metric on the product manifold, the conventional Low Rank Representation (LRR) model is extended onto PGM and the new LRR model can be used for clustering non-linear data, such as multi-camera video data. To evaluate the proposed method, a number of clustering experiments are conducted on several multi-camera video datasets of human activity, including Dongzhimen Transport Hub Crowd action dataset, ACT 42 Human action dataset and SKIG action dataset. The experiment results show that the proposed method outperforms many state-of-the-art clustering methods.

Kernelized LRR on Grassmann Manifolds for Subspace Clustering

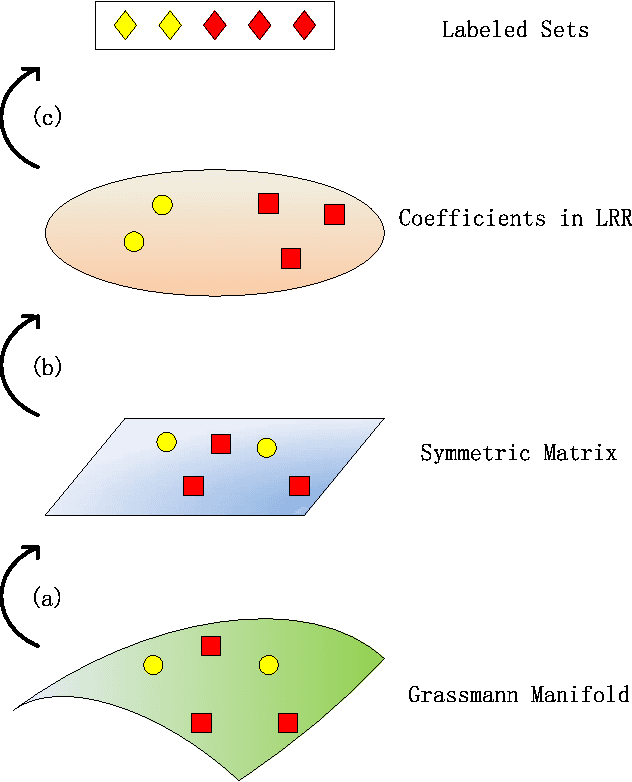
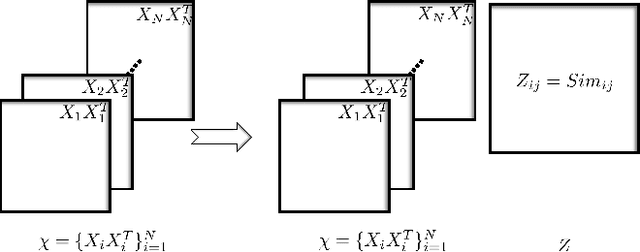
Low rank representation (LRR) has recently attracted great interest due to its pleasing efficacy in exploring low-dimensional sub- space structures embedded in data. One of its successful applications is subspace clustering, by which data are clustered according to the subspaces they belong to. In this paper, at a higher level, we intend to cluster subspaces into classes of subspaces. This is naturally described as a clustering problem on Grassmann manifold. The novelty of this paper is to generalize LRR on Euclidean space onto an LRR model on Grassmann manifold in a uniform kernelized LRR framework. The new method has many applications in data analysis in computer vision tasks. The proposed models have been evaluated on a number of practical data analysis applications. The experimental results show that the proposed models outperform a number of state-of-the-art subspace clustering methods.

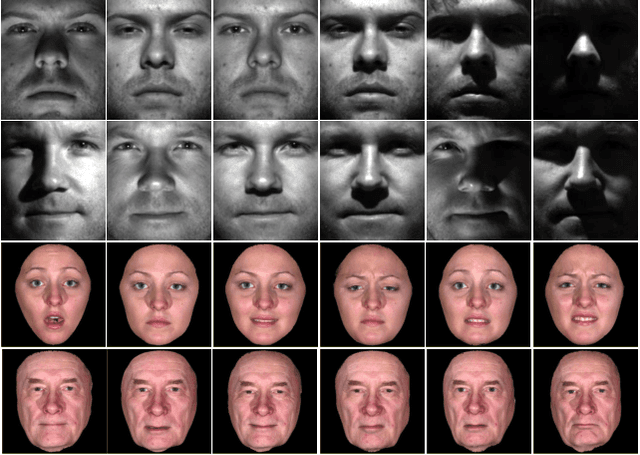
Mixture of Bilateral-Projection Two-dimensional Probabilistic Principal Component Analysis

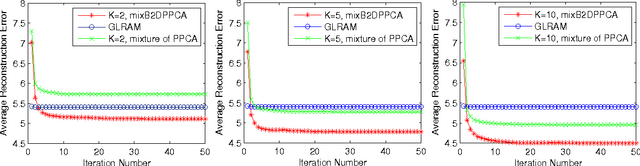
The probabilistic principal component analysis (PPCA) is built upon a global linear mapping, with which it is insufficient to model complex data variation. This paper proposes a mixture of bilateral-projection probabilistic principal component analysis model (mixB2DPPCA) on 2D data. With multi-components in the mixture, this model can be seen as a soft cluster algorithm and has capability of modeling data with complex structures. A Bayesian inference scheme has been proposed based on the variational EM (Expectation-Maximization) approach for learning model parameters. Experiments on some publicly available databases show that the performance of mixB2DPPCA has been largely improved, resulting in more accurate reconstruction errors and recognition rates than the existing PCA-based algorithms.

Matrix Variate RBM and Its Applications

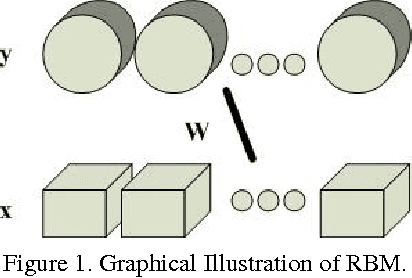
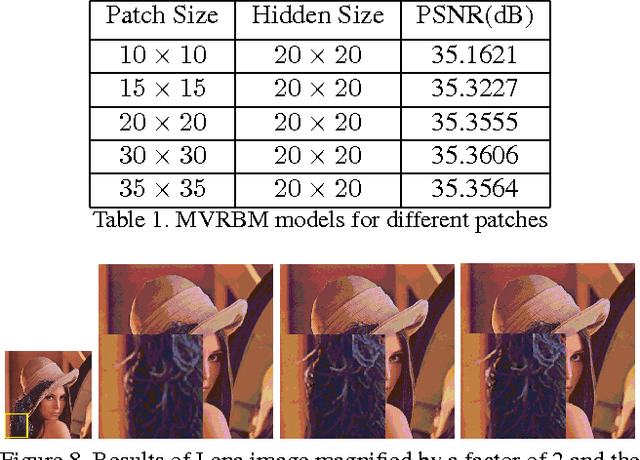
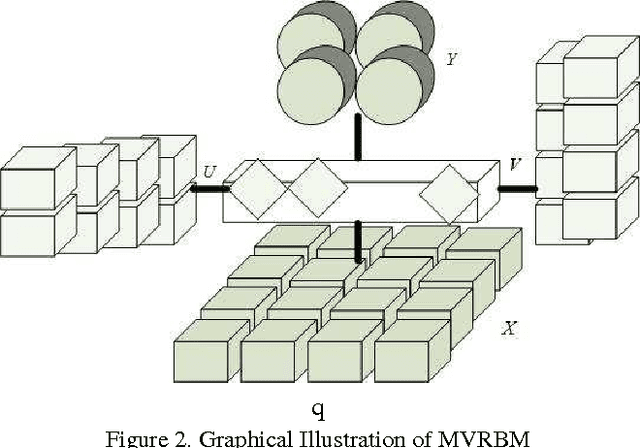
Restricted Boltzmann Machine (RBM) is an importan- t generative model modeling vectorial data. While applying an RBM in practice to images, the data have to be vec- torized. This results in high-dimensional data and valu- able spatial information has got lost in vectorization. In this paper, a Matrix-Variate Restricted Boltzmann Machine (MVRBM) model is proposed by generalizing the classic RBM to explicitly model matrix data. In the new RBM model, both input and hidden variables are in matrix forms which are connected by bilinear transforms. The MVRBM has much less model parameters, resulting in a faster train- ing algorithm while retaining comparable performance as the classic RBM. The advantages of the MVRBM have been demonstrated on two real-world applications: Image super- resolution and handwritten digit recognition.

Fast Optimization Algorithm on Riemannian Manifolds and Its Application in Low-Rank Representation

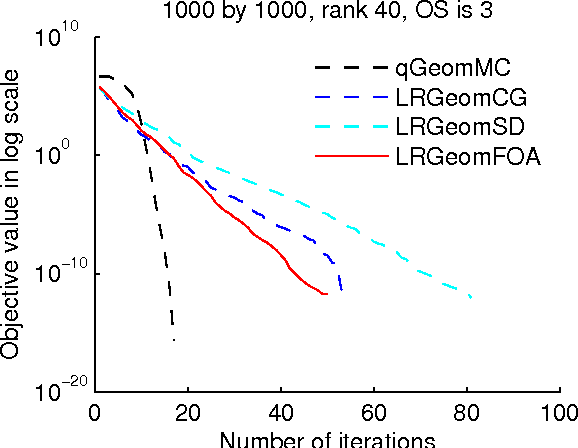
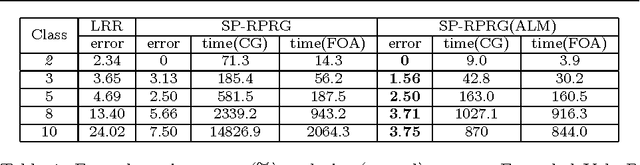
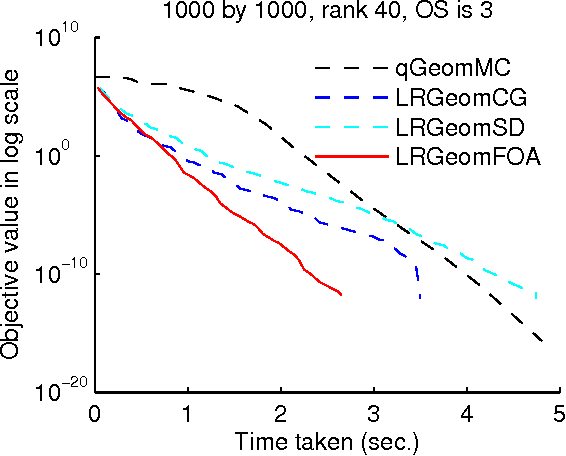
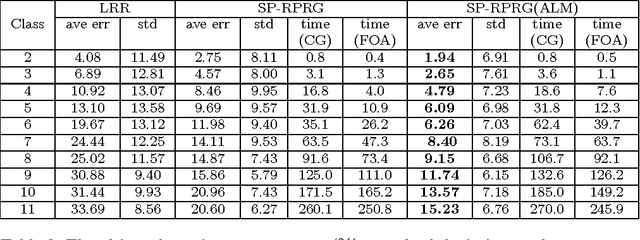
The paper addresses the problem of optimizing a class of composite functions on Riemannian manifolds and a new first order optimization algorithm (FOA) with a fast convergence rate is proposed. Through the theoretical analysis for FOA, it has been proved that the algorithm has quadratic convergence. The experiments in the matrix completion task show that FOA has better performance than other first order optimization methods on Riemannian manifolds. A fast subspace pursuit method based on FOA is proposed to solve the low-rank representation model based on augmented Lagrange method on the low rank matrix variety. Experimental results on synthetic and real data sets are presented to demonstrate that both FOA and SP-RPRG(ALM) can achieve superior performance in terms of faster convergence and higher accuracy.