BAMBO: Construct Ability and Efficiency LLM Pareto Set via Bayesian Adaptive Multi-objective Block-wise Optimization

Constructing a Pareto set is pivotal for navigating the capability-efficiency trade-offs in Large Language Models (LLMs); however, existing merging techniques remain inadequate for this task. Coarse-grained, model-level methods yield only a sparse set of suboptimal solutions, while fine-grained, layer-wise approaches suffer from the "curse of dimensionality," rendering the search space computationally intractable. To resolve this dichotomy, we propose BAMBO (Bayesian Adaptive Multi-objective Block-wise Optimization), a novel framework that automatically constructs the LLM Pareto set. BAMBO renders the search tractable by introducing a Hybrid Optimal Block Partitioning strategy. Formulated as a 1D clustering problem, this strategy leverages a dynamic programming approach to optimally balance intra-block homogeneity and inter-block information distribution, thereby dramatically reducing dimensionality without sacrificing critical granularity. The entire process is automated within an evolutionary loop driven by the q-Expected Hypervolume Improvement (qEHVI) acquisition function. Experiments demonstrate that BAMBO discovers a superior and more comprehensive Pareto frontier than baselines, enabling agile model selection tailored to diverse operational constraints. Code is available at: https://github.com/xin8coder/BAMBO.

Community-based 3-SAT Formulas with a Predefined Solution

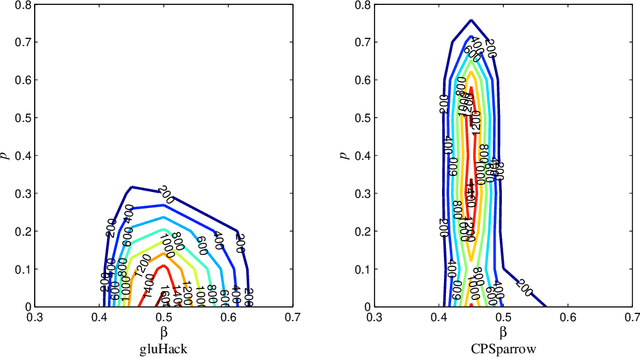
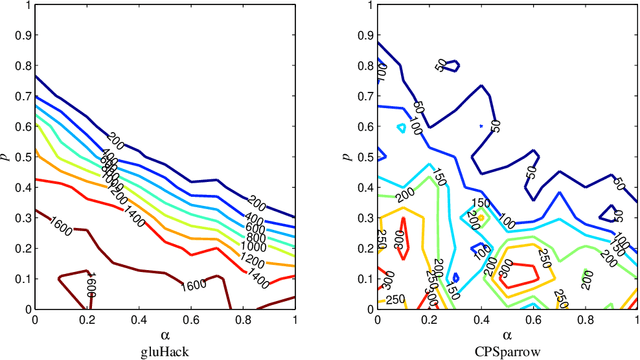
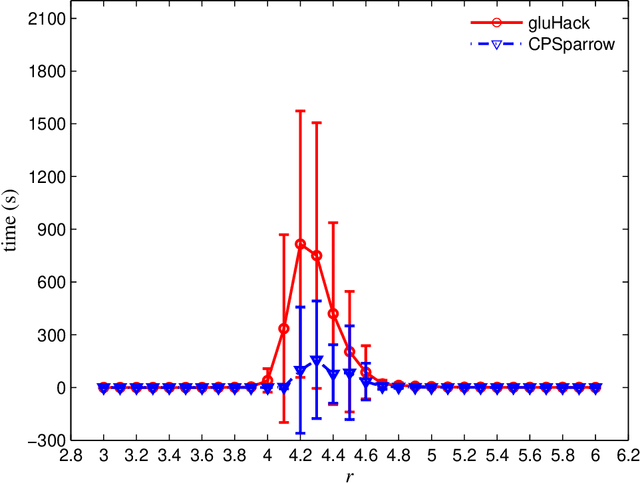
It is crucial to generate crafted SAT formulas with predefined solutions for the testing and development of SAT solvers since many SAT formulas from real-world applications have solutions. Although some generating algorithms have been proposed to generate SAT formulas with predefined solutions, community structures of SAT formulas are not considered. We propose a 3-SAT formula generating algorithm that not only guarantees the existence of a predefined solution, but also simultaneously considers community structures and clause distributions. The proposed 3-SAT formula generating algorithm controls the quality of community structures through controlling (1) the number of clauses whose variables have a common community, which we call intra-community clauses, and (2) the number of variables that only belong to one community, which we call intra-community variables. To study the combined effect of community structures and clause distributions on the hardness of SAT formulas, we measure solving runtimes of two solvers, gluHack (a leading CDCL solver) and CPSparrow (a leading SLS solver), on the generated SAT formulas under different groups of parameter settings. Through extensive experiments, we obtain some noteworthy observations on the SAT formulas generated by the proposed algorithm: (1) The community structure has little or no effects on the hardness of SAT formulas with regard to CPSparrow but a strong effect with regard to gluHack. (2) Only when the proportion of true literals in a SAT formula in terms of the predefined solution is 0.5, SAT formulas are hard-to-solve with regard to gluHack; when this proportion is below 0.5, SAT formulas are hard-to-solve with regard to CPSparrow. (3) When the ratio of the number of clauses to that of variables is around 4.25, the SAT formulas are hard-to-solve with regard to both gluHack and CPSparrow.