Fast Gibbs Sampling on Bayesian Hidden Markov Model with Missing Observations

The Hidden Markov Model (HMM) is a widely-used statistical model for handling sequential data. However, the presence of missing observations in real-world datasets often complicates the application of the model. The EM algorithm and Gibbs samplers can be used to estimate the model, yet suffering from various problems including non-convexity, high computational complexity and slow mixing. In this paper, we propose a collapsed Gibbs sampler that efficiently samples from HMMs' posterior by integrating out both the missing observations and the corresponding latent states. The proposed sampler is fast due to its three advantages. First, it achieves an estimation accuracy that is comparable to existing methods. Second, it can produce a larger Effective Sample Size (ESS) per iteration, which can be justified theoretically and numerically. Third, when the number of missing entries is large, the sampler has a significant smaller computational complexity per iteration compared to other methods, thus is faster computationally. In summary, the proposed sampling algorithm is fast both computationally and theoretically and is particularly advantageous when there are a lot of missing entries. Finally, empirical evaluations based on numerical simulations and real data analysis demonstrate that the proposed algorithm consistently outperforms existing algorithms in terms of time complexity and sampling efficiency (measured in ESS).

Appearance-free Tripartite Matching for Multiple Object Tracking

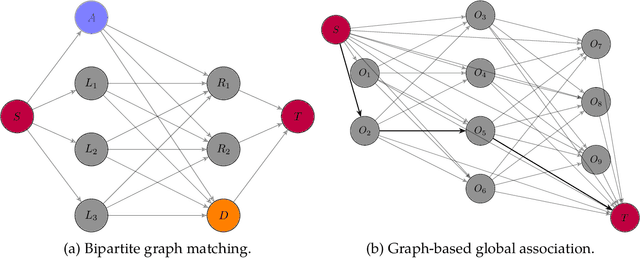
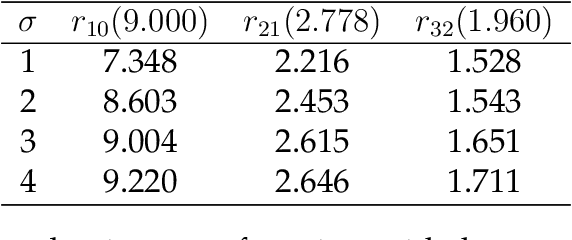
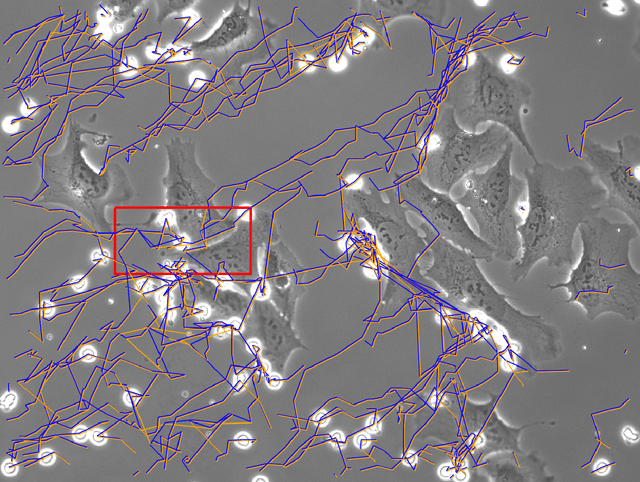
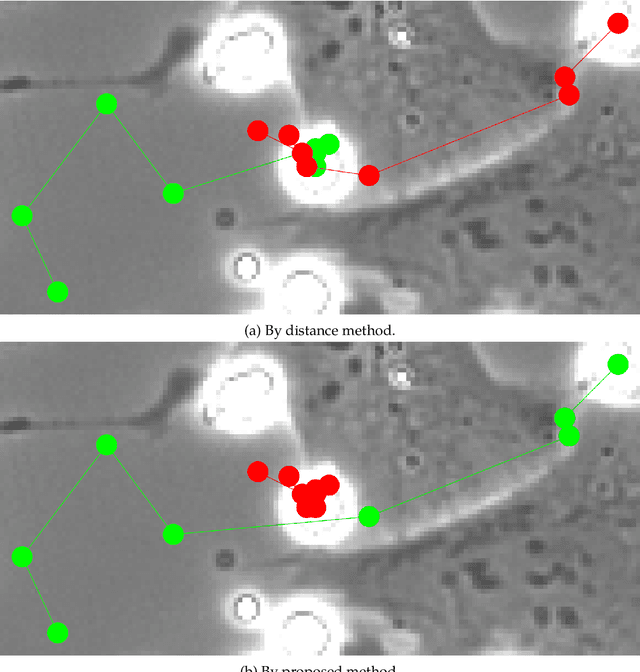
Multiple Object Tracking (MOT) detects the trajectories of multiple objects given an input video, and it has become more and more popular in various research and industry areas, such as cell tracking for biomedical research and human tracking in video surveillance. We target at the general MOT problem regardless of the object appearance. The appearance-free tripartite matching is proposed to avoid the irregular velocity problem of traditional bipartite matching. The tripartite matching is formulated as maximizing the likelihood of the state vectors constituted of the position and velocity of objects, and a dynamic programming algorithm is employed to solve such maximum likelihood estimate (MLE). To overcome the high computational cost induced by the vast search space of dynamic programming, we decompose the space by the number of disappearing objects and propose a reduced-space approach by truncating the decomposition. Extensive simulations have shown the superiority and efficiency of our proposed method. We also applied our method to track the motion of natural killer cells around tumor cells in a cancer research.

A Bayesian Method for Joint Clustering of Vectorial Data and Network Data

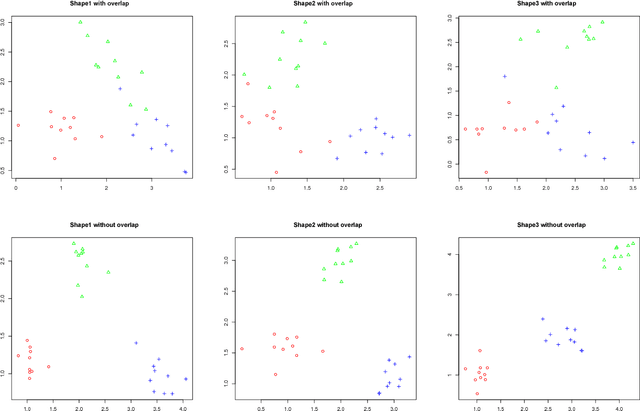
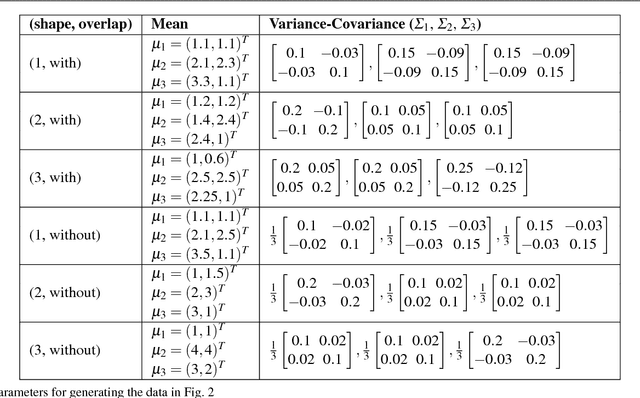
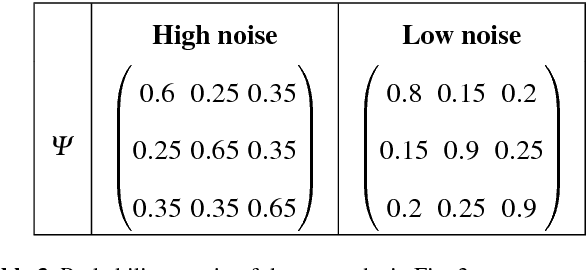
We present a new model-based integrative method for clustering objects given both vectorial data, which describes the feature of each object, and network data, which indicates the similarity of connected objects. The proposed general model is able to cluster the two types of data simultaneously within one integrative probabilistic model, while traditional methods can only handle one data type or depend on transforming one data type to another. Bayesian inference of the clustering is conducted based on a Markov chain Monte Carlo algorithm. A special case of the general model combining the Gaussian mixture model and the stochastic block model is extensively studied. We used both synthetic data and real data to evaluate this new method and compare it with alternative methods. The results show that our simultaneous clustering method performs much better. This improvement is due to the power of the model-based probabilistic approach for efficiently integrating information.