Asymptotically Optimal Pure Exploration for Infinite-Armed Bandits

We study pure exploration with infinitely many bandit arms generated i.i.d. from an unknown distribution. Our goal is to efficiently select a single high quality arm whose average reward is, with probability $1-\delta$, within $\varepsilon$ of being among the top $\eta$-fraction of arms; this is a natural adaptation of the classical PAC guarantee for infinite action sets. We consider both the fixed confidence and fixed budget settings, aiming respectively for minimal expected and fixed sample complexity. For fixed confidence, we give an algorithm with expected sample complexity $O\left(\frac{\log (1/\eta)\log (1/\delta)}{\eta\varepsilon^2}\right)$. This is optimal except for the $\log (1/\eta)$ factor, and the $\delta$-dependence closes a quadratic gap in the literature. For fixed budget, we show the asymptotically optimal sample complexity as $\delta\to 0$ is $c^{-1}\log(1/\delta)\big(\log\log(1/\delta)\big)^2$ to leading order. Equivalently, the optimal failure probability given exactly $N$ samples decays as $\exp\big(-cN/\log^2 N\big)$, up to a factor $1\pm o_N(1)$ inside the exponent. The constant $c$ depends explicitly on the problem parameters (including the unknown arm distribution) through a certain Fisher information distance. Even the strictly super-linear dependence on $\log(1/\delta)$ was not known and resolves a question of Grossman and Moshkovitz (FOCS 2016, SIAM Journal on Computing 2020).

Provably More Efficient Q-Learning in the Full-Feedback/One-Sided-Feedback Settings

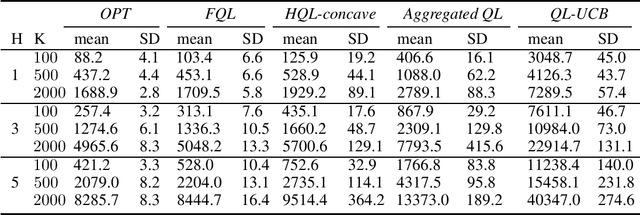
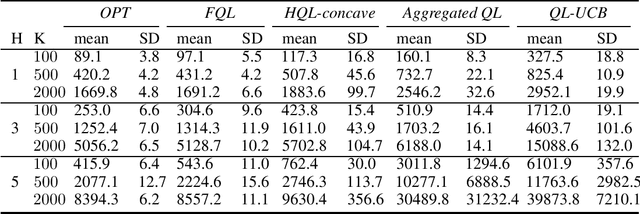
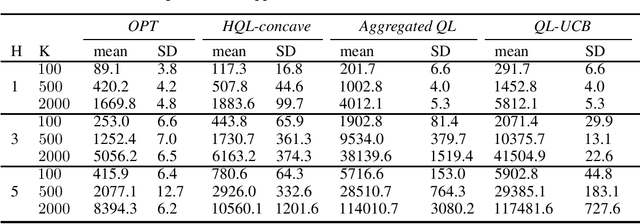
We propose two new Q-learning algorithms, Full-Q-Learning (FQL) and Elimination-Based Half-Q-Learning (HQL), that enjoy improved efficiency and optimality in the full-feedback and the one-sided-feedback settings over existing Q-learning algorithms. We establish that FQL incurs regret $\tilde{O}(H^2\sqrt{ T})$ and HQL incurs regret $ \tilde{O}(H^3\sqrt{ T})$, where $H$ is the length of each episode and $T$ is the total number of time periods. Our regret bounds are not affected by the possibly huge state and action space. Our numerical experiments using the classical inventory control problem as an example demonstrate the superior efficiency of FQL and HQL, and shows the potential of tailoring reinforcement learning algorithms for richer feedback models, which are prevalent in many natural problems.

Efficient Entropy for Policy Gradient with Multidimensional Action Space

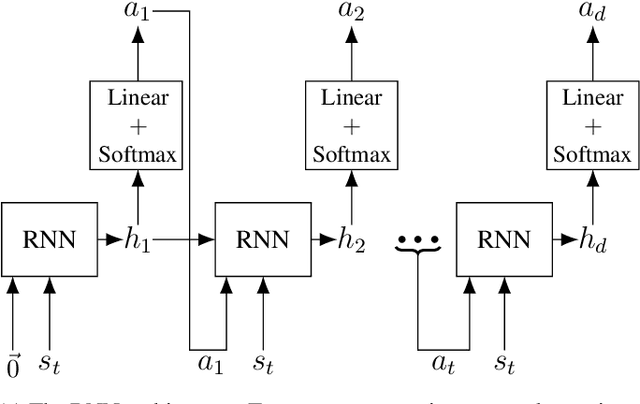
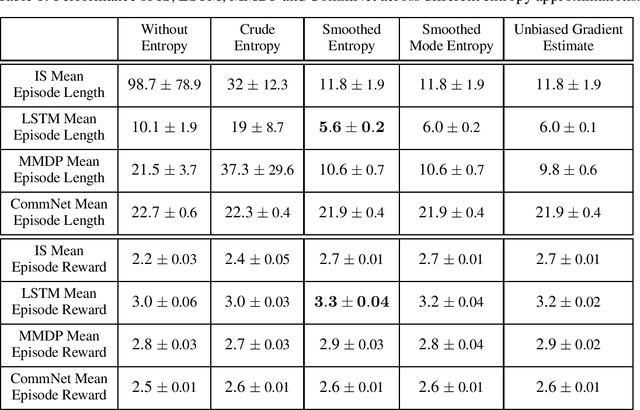
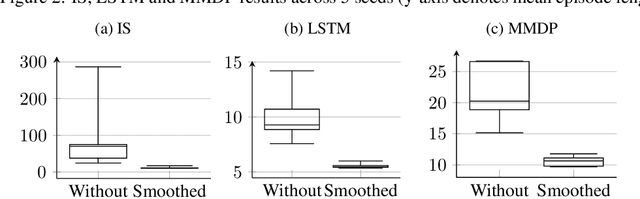
In recent years, deep reinforcement learning has been shown to be adept at solving sequential decision processes with high-dimensional state spaces such as in the Atari games. Many reinforcement learning problems, however, involve high-dimensional discrete action spaces as well as high-dimensional state spaces. This paper considers entropy bonus, which is used to encourage exploration in policy gradient. In the case of high-dimensional action spaces, calculating the entropy and its gradient requires enumerating all the actions in the action space and running forward and backpropagation for each action, which may be computationally infeasible. We develop several novel unbiased estimators for the entropy bonus and its gradient. We apply these estimators to several models for the parameterized policies, including Independent Sampling, CommNet, Autoregressive with Modified MDP, and Autoregressive with LSTM. Finally, we test our algorithms on two environments: a multi-hunter multi-rabbit grid game and a multi-agent multi-arm bandit problem. The results show that our entropy estimators substantially improve performance with marginal additional computational cost.