Enhancing Polynomial Chaos Expansion Based Surrogate Modeling using a Novel Probabilistic Transfer Learning Strategy

In the field of surrogate modeling, polynomial chaos expansion (PCE) allows practitioners to construct inexpensive yet accurate surrogates to be used in place of the expensive forward model simulations. For black-box simulations, non-intrusive PCE allows the construction of these surrogates using a set of simulation response evaluations. In this context, the PCE coefficients can be obtained using linear regression, which is also known as point collocation or stochastic response surfaces. Regression exhibits better scalability and can handle noisy function evaluations in contrast to other non-intrusive approaches, such as projection. However, since over-sampling is generally advisable for the linear regression approach, the simulation requirements become prohibitive for expensive forward models. We propose to leverage transfer learning whereby knowledge gained through similar PCE surrogate construction tasks (source domains) is transferred to a new surrogate-construction task (target domain) which has a limited number of forward model simulations (training data). The proposed transfer learning strategy determines how much, if any, information to transfer using new techniques inspired by Bayesian modeling and data assimilation. The strategy is scrutinized using numerical investigations and applied to an engineering problem from the oil and gas industry.

Robust scalable initialization for Bayesian variational inference with multi-modal Laplace approximations

For predictive modeling relying on Bayesian inversion, fully independent, or ``mean-field'', Gaussian distributions are often used as approximate probability density functions in variational inference since the number of variational parameters is twice the number of unknown model parameters. The resulting diagonal covariance structure coupled with unimodal behavior can be too restrictive when dealing with highly non-Gaussian behavior, including multimodality. High-fidelity surrogate posteriors in the form of Gaussian mixtures can capture any distribution to an arbitrary degree of accuracy while maintaining some analytical tractability. Variational inference with Gaussian mixtures with full-covariance structures suffers from a quadratic growth in variational parameters with the number of model parameters. Coupled with the existence of multiple local minima due to nonconvex trends in the loss functions often associated with variational inference, these challenges motivate the need for robust initialization procedures to improve the performance and scalability of variational inference with mixture models. In this work, we propose a method for constructing an initial Gaussian mixture model approximation that can be used to warm-start the iterative solvers for variational inference. The procedure begins with an optimization stage in model parameter space in which local gradient-based optimization, globalized through multistart, is used to determine a set of local maxima, which we take to approximate the mixture component centers. Around each mode, a local Gaussian approximation is constructed via the Laplace method. Finally, the mixture weights are determined through constrained least squares regression. Robustness and scalability are demonstrated using synthetic tests. The methodology is applied to an inversion problem in structural dynamics involving unknown viscous damping coefficients.

A heteroencoder architecture for prediction of failure locations in porous metals using variational inference

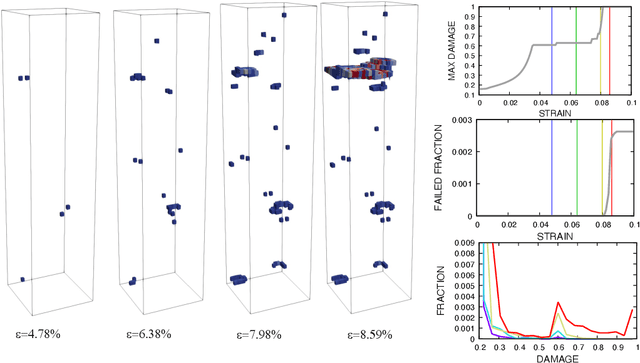
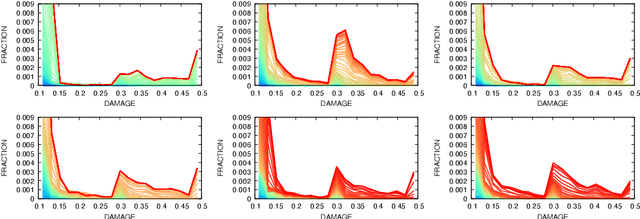
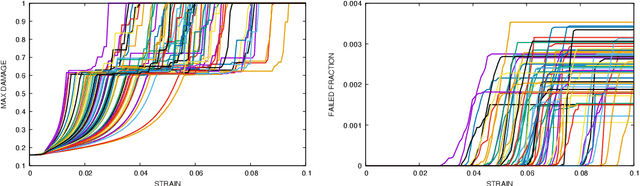
In this work we employ an encoder-decoder convolutional neural network to predict the failure locations of porous metal tension specimens based only on their initial porosities. The process we model is complex, with a progression from initial void nucleation, to saturation, and ultimately failure. The objective of predicting failure locations presents an extreme case of class imbalance since most of the material in the specimens do not fail. In response to this challenge, we develop and demonstrate the effectiveness of data- and loss-based regularization methods. Since there is considerable sensitivity of the failure location to the particular configuration of voids, we also use variational inference to provide uncertainties for the neural network predictions. We connect the deterministic and Bayesian convolutional neural networks at a theoretical level to explain how variational inference regularizes the training and predictions. We demonstrate that the resulting predicted variances are effective in ranking the locations that are most likely to fail in any given specimen.