Xuqing Wu
Enhancing Polynomial Chaos Expansion Based Surrogate Modeling using a Novel Probabilistic Transfer Learning Strategy
Dec 07, 2023



Abstract:In the field of surrogate modeling, polynomial chaos expansion (PCE) allows practitioners to construct inexpensive yet accurate surrogates to be used in place of the expensive forward model simulations. For black-box simulations, non-intrusive PCE allows the construction of these surrogates using a set of simulation response evaluations. In this context, the PCE coefficients can be obtained using linear regression, which is also known as point collocation or stochastic response surfaces. Regression exhibits better scalability and can handle noisy function evaluations in contrast to other non-intrusive approaches, such as projection. However, since over-sampling is generally advisable for the linear regression approach, the simulation requirements become prohibitive for expensive forward models. We propose to leverage transfer learning whereby knowledge gained through similar PCE surrogate construction tasks (source domains) is transferred to a new surrogate-construction task (target domain) which has a limited number of forward model simulations (training data). The proposed transfer learning strategy determines how much, if any, information to transfer using new techniques inspired by Bayesian modeling and data assimilation. The strategy is scrutinized using numerical investigations and applied to an engineering problem from the oil and gas industry.
First arrival picking using U-net with Lovasz loss and nearest point picking method
Apr 06, 2021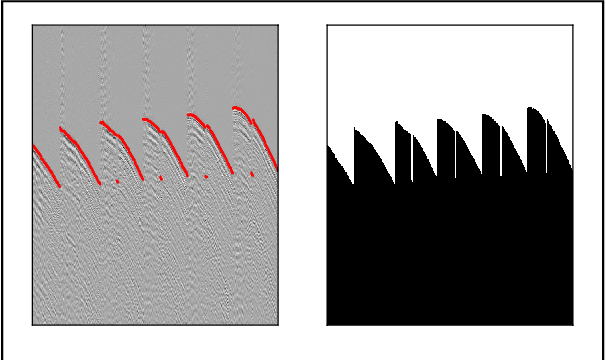
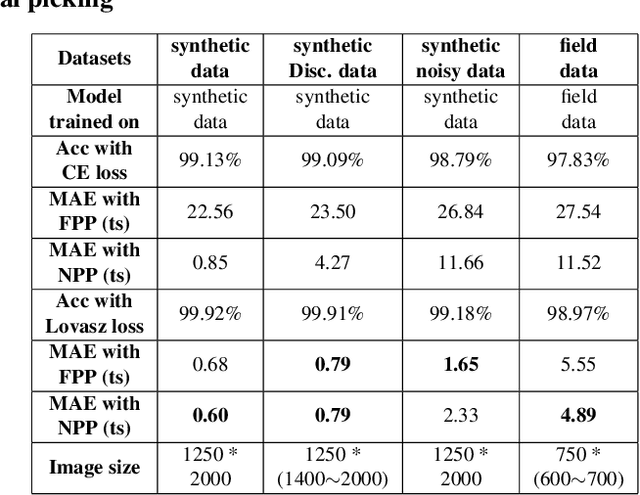
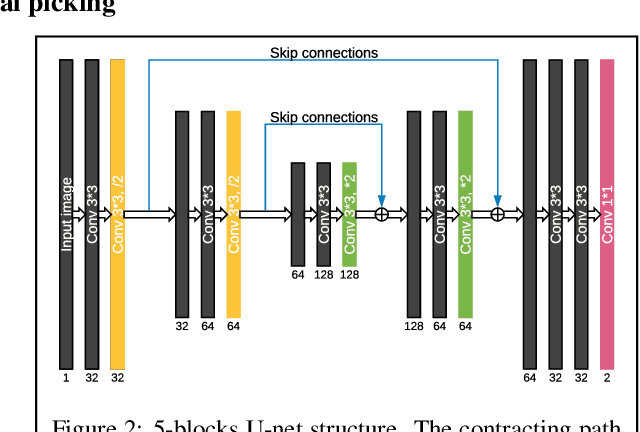
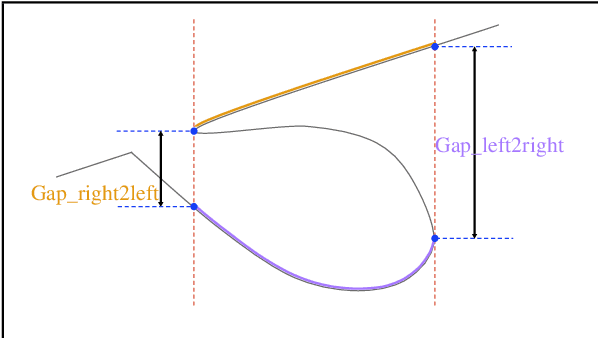
Abstract:We proposed a robust segmentation and picking workflow to solve the first arrival picking problem for seismic signal processing. Unlike traditional classification algorithm, image segmentation method can utilize the location information by outputting a prediction map which has the same size of the input image. A parameter-free nearest point picking algorithm is proposed to further improve the accuracy of the first arrival picking. The algorithm is test on synthetic clean data, synthetic noisy data, synthetic picking-disconnected data and field data. It performs well on all of them and the picking deviation reaches as low as 4.8ms per receiver. The first arrival picking problem is formulated as the contour detection problem. Similar to \cite{wu2019semi}, we use U-net to perform the segmentation as it is proven to be state-of-the-art in many image segmentation tasks. Particularly, a Lovasz loss instead of the traditional cross-entropy loss is used to train the network for a better segmentation performance. Lovasz loss is a surrogate loss for Jaccard index or the so-called intersection-over-union (IoU) score, which is often one of the most used metrics for segmentation tasks. In the picking part, we use a novel nearest point picking (NPP) method to take the advantage of the coherence of the first arrival picking among adjacent receivers. Our model is tested and validated on both synthetic and field data with harmonic noises. The main contributions of this paper are as follows: 1. Used Lovasz loss to directly optimize the IoU for segmentation task. Improvement over the cross-entropy loss with regard to the segmentation accuracy is verified by the test result. 2. Proposed a nearest point picking post processing method to overcome any defects left by the segmentation output. 3. Conducted noise analysis and verified the model with both noisy synthetic and field datasets.
Progressive transfer learning for low frequency data prediction in full waveform inversion
Dec 20, 2019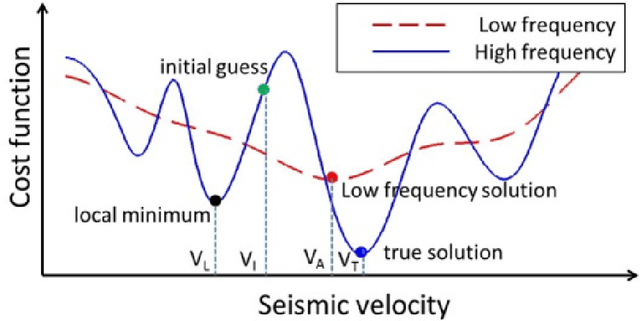
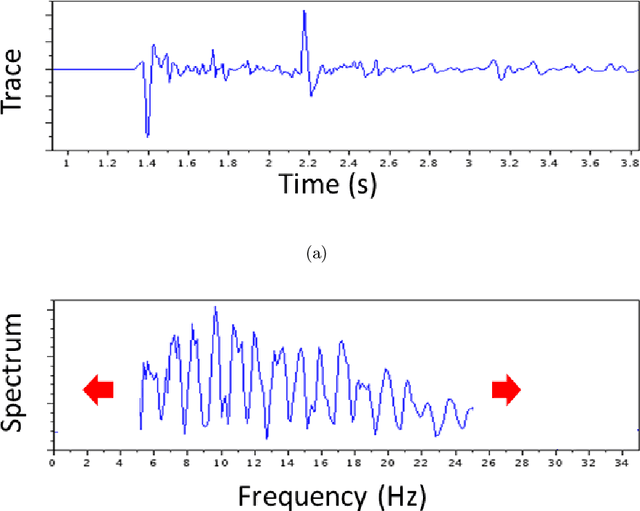

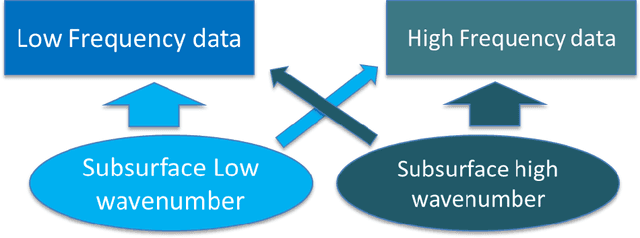
Abstract:For the purpose of effective suppression of the cycle-skipping phenomenon in full waveform inversion (FWI), we developed a Deep Neural Network (DNN) approach to predict the absent low-frequency components by exploiting the implicit relation connecting the low-frequency and high-frequency data through the subsurface geological and geophysical properties. In order to solve this challenging nonlinear regression problem, two novel strategies were proposed to design the DNN architecture and the learning workflow: 1) Dual Data Feed; 2) Progressive Transfer Learning. With the Dual Data Feed structure, both the high-frequency data and the corresponding Beat Tone data are fed into the DNN to relieve the burden of feature extraction, thus reducing the network complexity and the training cost. The second strategy, Progressive Transfer Learning, enables us to unbiasedly train the DNN using a single training dataset. Unlike most established deep learning approaches where the training datasets are fixed, within the framework of the Progressive Transfer Learning, the training dataset evolves in an iterative manner while gradually absorbing the subsurface information retrieved by the physics-based inversion module, progressively enhancing the prediction accuracy of the DNN and propelling the FWI process out of the local minima. The Progressive Transfer Learning, alternatingly updating the training velocity model and the DNN parameters in a complementary fashion toward convergence, saves us from being overwhelmed by the otherwise tremendous amount of training data, and avoids the underfitting and biased sampling issues. The numerical experiments validated that, without any a priori geological information, the low-frequency data predicted by the Progressive Transfer Learning are sufficiently accurate for an FWI engine to produce reliable subsurface velocity models free of cycle-skipping-induced artifacts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge