TOMA: Topological Map Abstraction for Reinforcement Learning

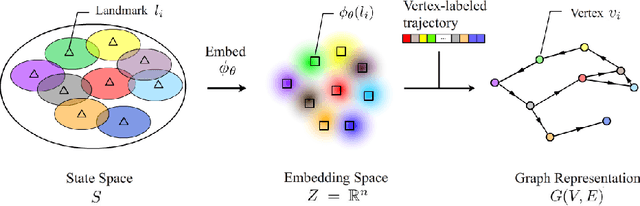
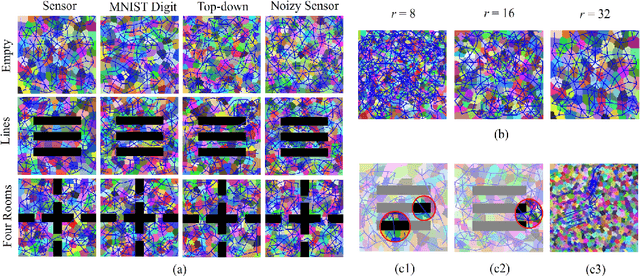
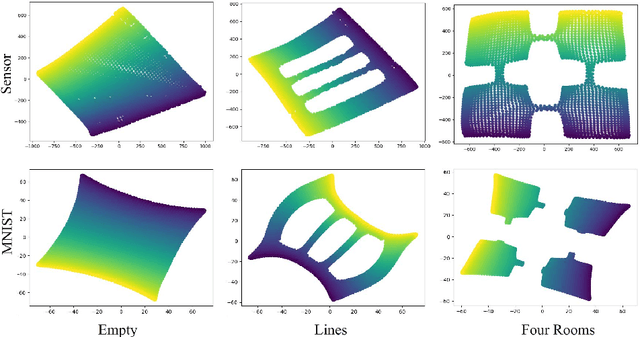
Animals are able to discover the topological map (graph) of surrounding environment, which will be used for navigation. Inspired by this biological phenomenon, researchers have recently proposed to generate topological map (graph) representation for Markov decision process (MDP) and use such graphs for planning in reinforcement learning (RL). However, existing graph generation methods suffer from many drawbacks. One drawback is that existing methods do not learn an abstraction for graphs, which results in high memory cost. Another drawback is that these existing methods can only work in some specific settings, which limits their application. In this paper, we propose a new method, called TOpological Map Abstraction (TOMA), for graph generation. TOMA can generate an abstract graph representation for MDP, which costs much less memory than existing methods. Furthermore, the generated graphs of TOMA can be used as a basic multi-purpose tool for different RL applications. As an application example, we propose planning to explore, in which TOMA is used to accelerate exploration by guiding the agent towards unexplored states. A novel experience replay module called vertex memory is also proposed to improve exploration performance. Experimental results show that TOMA can robustly generate abstract graph representation on several 2D world environments with different types of observation. Under the guidance of such graph representation, the agent can escape local minima during exploration.

BASGD: Buffered Asynchronous SGD for Byzantine Learning

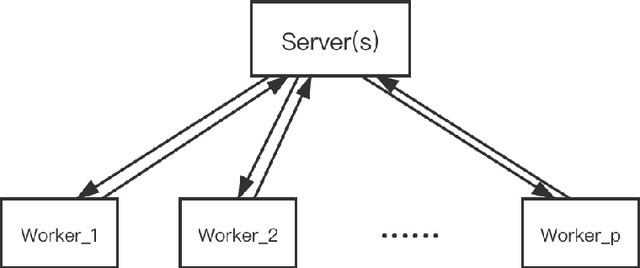
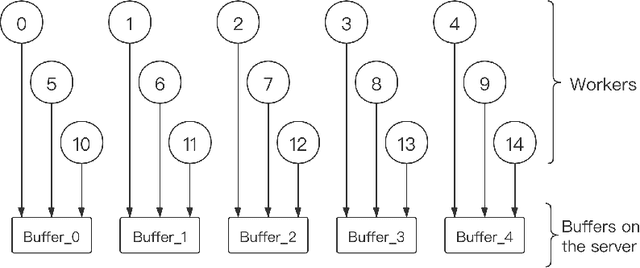
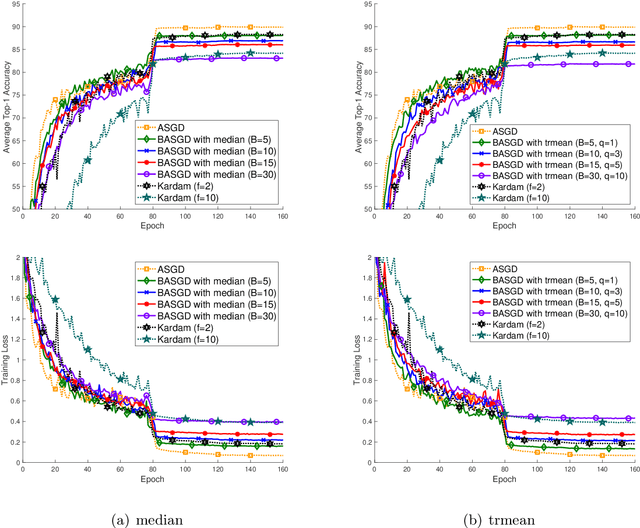
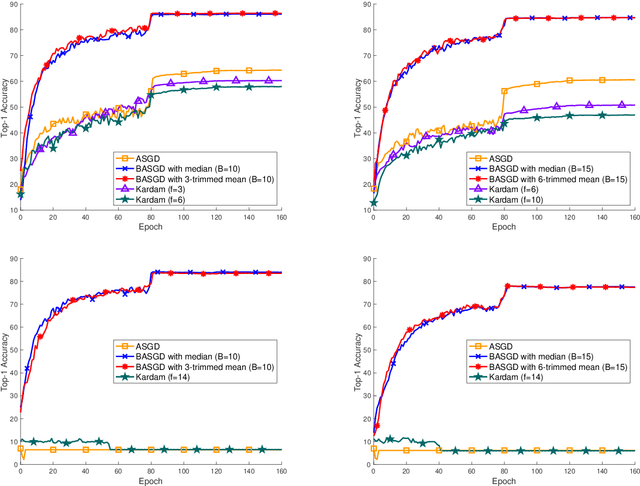
Distributed learning has become a hot research topic, due to its wide application in cluster-based large-scale learning, federated learning, edge computing and so on. Most distributed learning methods assume no error and attack on the workers. However, many unexpected cases, such as communication error and even malicious attack, may happen in real applications. Hence, Byzantine learning (BL), which refers to distributed learning with attack or error, has recently attracted much attention. Most existing BL methods are synchronous, which will result in slow convergence when there exist heterogeneous workers. Furthermore, in some applications like federated learning and edge computing, synchronization cannot even be performed most of the time due to the online workers (clients or edge servers). Hence, asynchronous BL (ABL) is more general and practical than synchronous BL (SBL). To the best of our knowledge, there exist only two ABL methods. One of them cannot resist malicious attack. The other needs to store some training instances on the server, which has the privacy leak problem. In this paper, we propose a novel method, called buffered asynchronous stochastic gradient descent (BASGD), for BL. BASGD is an asynchronous method. Furthermore, BASGD has no need to store any training instances on the server, and hence can preserve privacy in ABL. BASGD is theoretically proved to have the ability of resisting against error and malicious attack. Moreover, BASGD has a similar theoretical convergence rate to that of vanilla asynchronous SGD (ASGD), with an extra constant variance. Empirical results show that BASGD can significantly outperform vanilla ASGD and other ABL baselines, when there exists error or attack on workers.

Stagewise Enlargement of Batch Size for SGD-based Learning

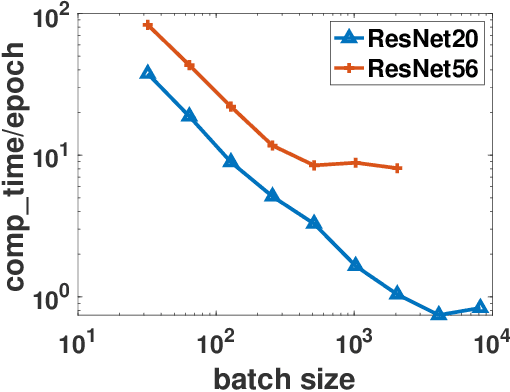
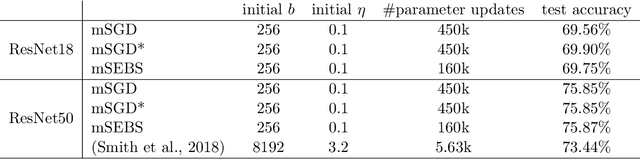
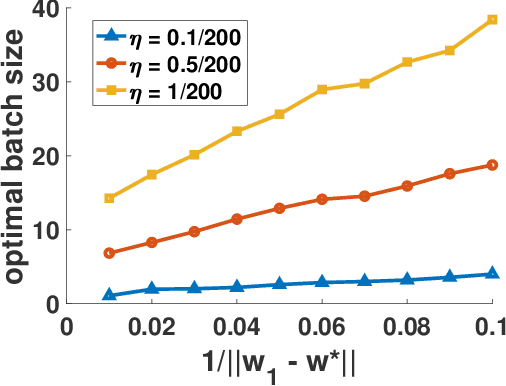
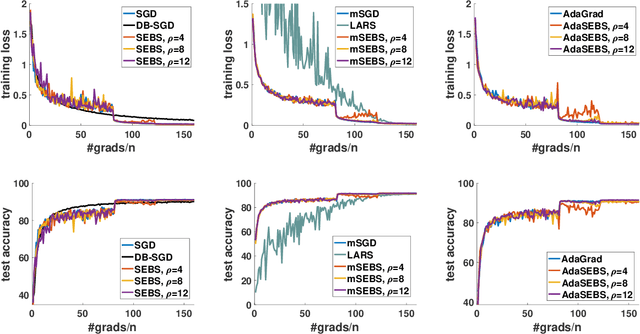
Existing research shows that the batch size can seriously affect the performance of stochastic gradient descent~(SGD) based learning, including training speed and generalization ability. A larger batch size typically results in less parameter updates. In distributed training, a larger batch size also results in less frequent communication. However, a larger batch size can make a generalization gap more easily. Hence, how to set a proper batch size for SGD has recently attracted much attention. Although some methods about setting batch size have been proposed, the batch size problem has still not been well solved. In this paper, we first provide theory to show that a proper batch size is related to the gap between initialization and optimum of the model parameter. Then based on this theory, we propose a novel method, called \underline{s}tagewise \underline{e}nlargement of \underline{b}atch \underline{s}ize~(\mbox{SEBS}), to set proper batch size for SGD. More specifically, \mbox{SEBS} adopts a multi-stage scheme, and enlarges the batch size geometrically by stage. We theoretically prove that, compared to classical stagewise SGD which decreases learning rate by stage, \mbox{SEBS} can reduce the number of parameter updates without increasing generalization error. SEBS is suitable for \mbox{SGD}, momentum \mbox{SGD} and AdaGrad. Empirical results on real data successfully verify the theories of \mbox{SEBS}. Furthermore, empirical results also show that SEBS can outperform other baselines.

Weight Normalization based Quantization for Deep Neural Network Compression

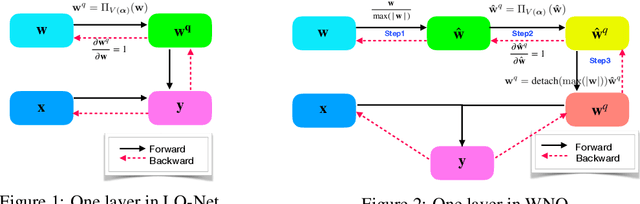
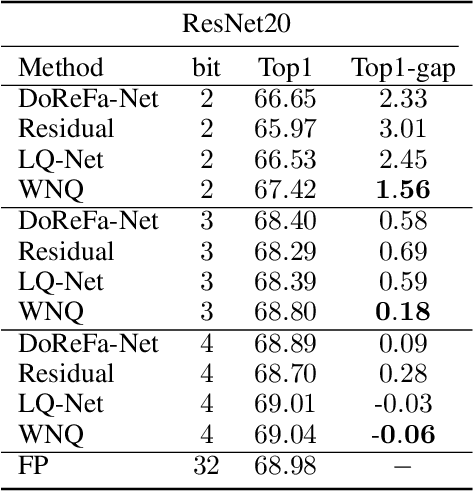
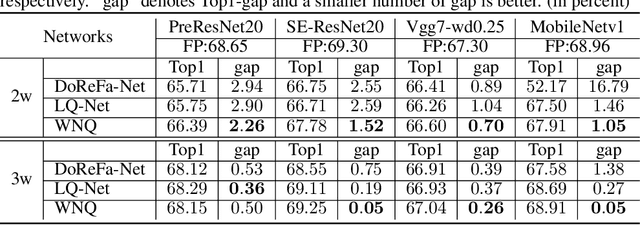
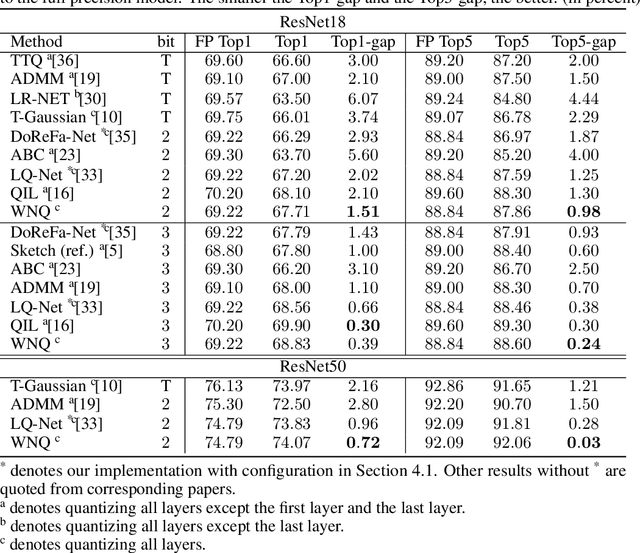
With the development of deep neural networks, the size of network models becomes larger and larger. Model compression has become an urgent need for deploying these network models to mobile or embedded devices. Model quantization is a representative model compression technique. Although a lot of quantization methods have been proposed, many of them suffer from a high quantization error caused by a long-tail distribution of network weights. In this paper, we propose a novel quantization method, called weight normalization based quantization (WNQ), for model compression. WNQ adopts weight normalization to avoid the long-tail distribution of network weights and subsequently reduces the quantization error. Experiments on CIFAR-100 and ImageNet show that WNQ can outperform other baselines to achieve state-of-the-art performance.

ADASS: Adaptive Sample Selection for Training Acceleration

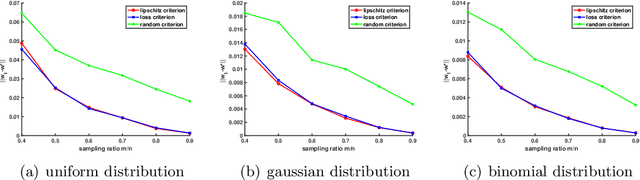
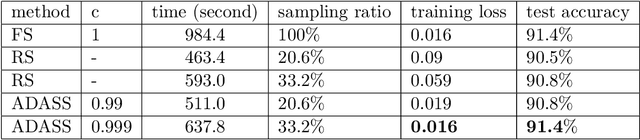
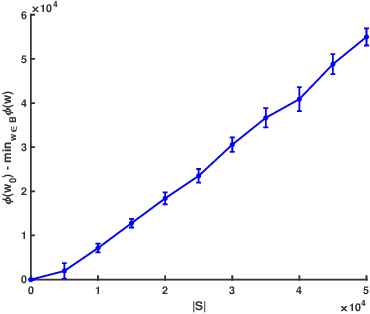
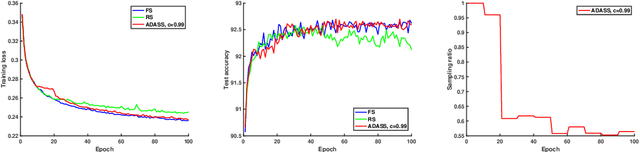
Stochastic gradient decent~(SGD) and its variants, including some accelerated variants, have become popular for training in machine learning. However, in all existing SGD and its variants, the sample size in each iteration~(epoch) of training is the same as the size of the full training set. In this paper, we propose a new method, called \underline{ada}ptive \underline{s}ample \underline{s}election~(ADASS), for training acceleration. During different epoches of training, ADASS only need to visit different training subsets which are adaptively selected from the full training set according to the Lipschitz constants of the loss functions on samples. It means that in ADASS the sample size in each epoch of training can be smaller than the size of the full training set, by discarding some samples. ADASS can be seamlessly integrated with existing optimization methods, such as SGD and momentum SGD, for training acceleration. Theoretical results show that the learning accuracy of ADASS is comparable to that of counterparts with full training set. Furthermore, empirical results on both shallow models and deep models also show that ADASS can accelerate the training process of existing methods without sacrificing accuracy.

Clustered Reinforcement Learning

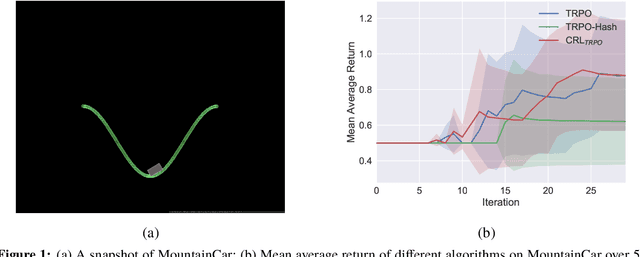
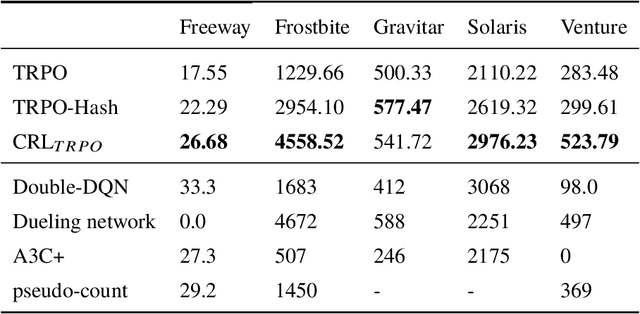
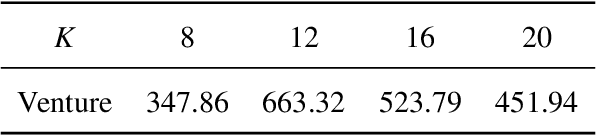
Exploration strategy design is one of the challenging problems in reinforcement learning~(RL), especially when the environment contains a large state space or sparse rewards. During exploration, the agent tries to discover novel areas or high reward~(quality) areas. In most existing methods, the novelty and quality in the neighboring area of the current state are not well utilized to guide the exploration of the agent. To tackle this problem, we propose a novel RL framework, called \underline{c}lustered \underline{r}einforcement \underline{l}earning~(CRL), for efficient exploration in RL. CRL adopts clustering to divide the collected states into several clusters, based on which a bonus reward reflecting both novelty and quality in the neighboring area~(cluster) of the current state is given to the agent. Experiments on a continuous control task and several \emph{Atari 2600} games show that CRL can outperform other state-of-the-art methods to achieve the best performance in most cases.

On the Convergence of Memory-Based Distributed SGD

Distributed stochastic gradient descent~(DSGD) has been widely used for optimizing large-scale machine learning models, including both convex and non-convex models. With the rapid growth of model size, huge communication cost has been the bottleneck of traditional DSGD. Recently, many communication compression methods have been proposed. Memory-based distributed stochastic gradient descent~(M-DSGD) is one of the efficient methods since each worker communicates a sparse vector in each iteration so that the communication cost is small. Recent works propose the convergence rate of M-DSGD when it adopts vanilla SGD. However, there is still a lack of convergence theory for M-DSGD when it adopts momentum SGD. In this paper, we propose a universal convergence analysis for M-DSGD by introducing \emph{transformation equation}. The transformation equation describes the relation between traditional DSGD and M-DSGD so that we can transform M-DSGD to its corresponding DSGD. Hence we get the convergence rate of M-DSGD with momentum for both convex and non-convex problems. Furthermore, we combine M-DSGD and stagewise learning that the learning rate of M-DSGD in each stage is a constant and is decreased by stage, instead of iteration. Using the transformation equation, we propose the convergence rate of stagewise M-DSGD which bridges the gap between theory and practice.

Global Momentum Compression for Sparse Communication in Distributed SGD

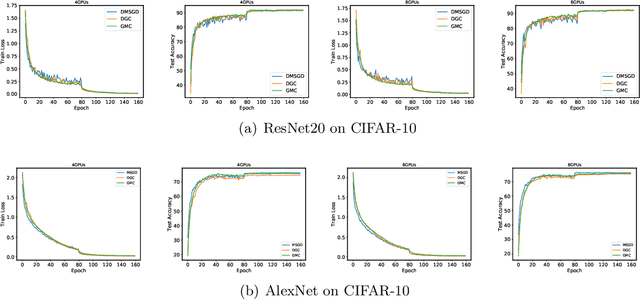
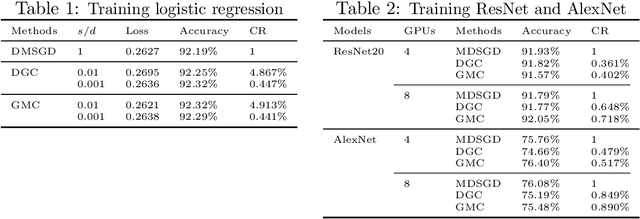
With the rapid growth of data, distributed stochastic gradient descent~(DSGD) has been widely used for solving large-scale machine learning problems. Due to the latency and limited bandwidth of network, communication has become the bottleneck of DSGD when we need to train large scale models, like deep neural networks. Communication compression with sparsified gradient, abbreviated as \emph{sparse communication}, has been widely used for reducing communication cost in DSGD. Recently, there has appeared one method, called deep gradient compression~(DGC), to combine memory gradient and momentum SGD for sparse communication. DGC has achieved promising performance in practise. However, the theory about the convergence of DGC is lack. In this paper, we propose a novel method, called \emph{\underline{g}}lobal \emph{\underline{m}}omentum \emph{\underline{c}}ompression~(GMC), for sparse communication in DSGD. GMC also combines memory gradient and momentum SGD. But different from DGC which adopts local momentum, GMC adopts global momentum. We theoretically prove the convergence rate of GMC for both convex and non-convex problems. To the best of our knowledge, this is the first work that proves the convergence of distributed momentum SGD~(DMSGD) with sparse communication and memory gradient. Empirical results show that, compared with the DMSGD counterpart without sparse communication, GMC can reduce the communication cost by approximately 100 fold without loss of generalization accuracy. GMC can also achieve comparable~(sometimes better) performance compared with DGC, with extra theoretical guarantee.

Deep Multi-Index Hashing for Person Re-Identification

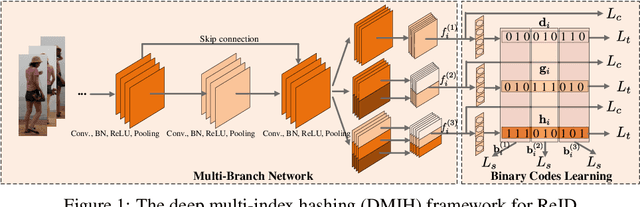
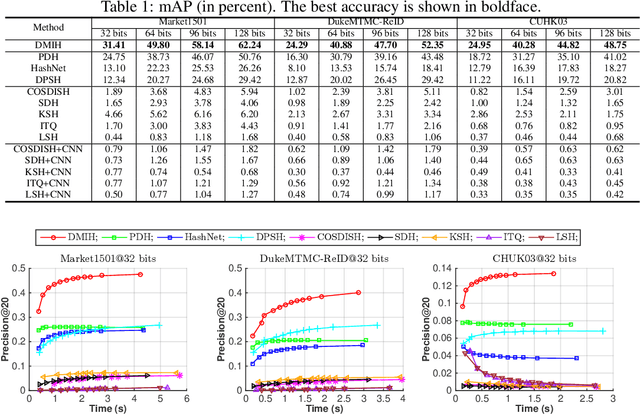
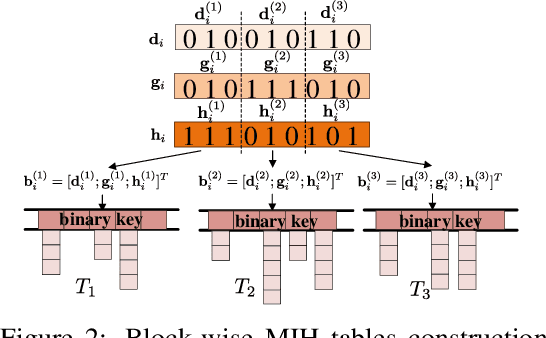
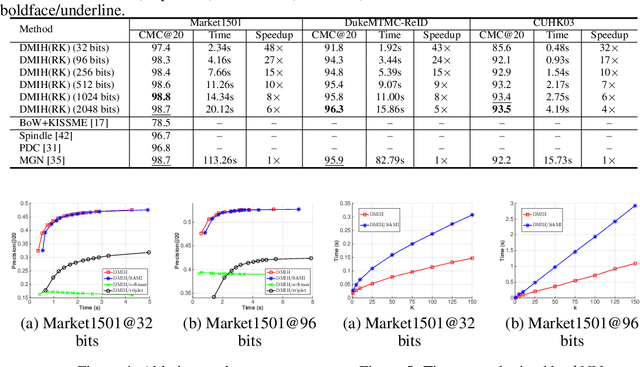
Traditional person re-identification (ReID) methods typically represent person images as real-valued features, which makes ReID inefficient when the gallery set is extremely large. Recently, some hashing methods have been proposed to make ReID more efficient. However, these hashing methods will deteriorate the accuracy in general, and the efficiency of them is still not high enough. In this paper, we propose a novel hashing method, called deep multi-index hashing (DMIH), to improve both efficiency and accuracy for ReID. DMIH seamlessly integrates multi-index hashing and multi-branch based networks into the same framework. Furthermore, a novel block-wise multi-index hashing table construction approach and a search-aware multi-index (SAMI) loss are proposed in DMIH to improve the search efficiency. Experiments on three widely used datasets show that DMIH can outperform other state-of-the-art baselines, including both hashing methods and real-valued methods, in terms of both efficiency and accuracy.

Collaborative Self-Attention for Recommender Systems

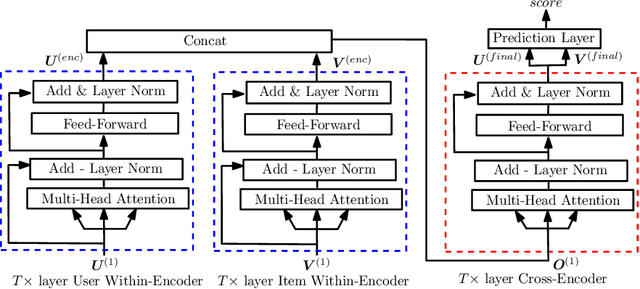
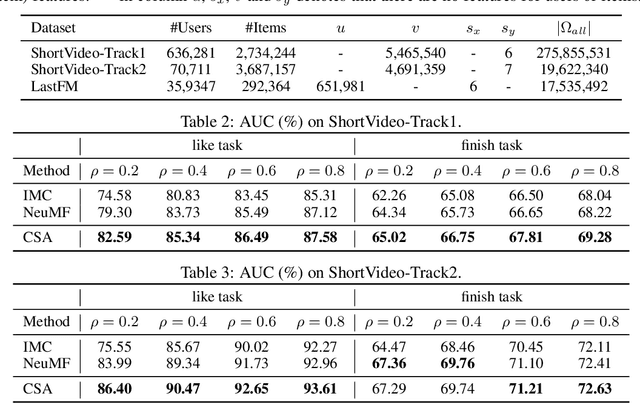
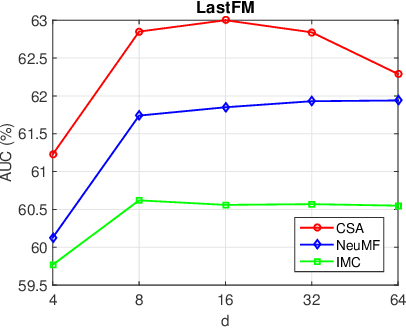
Recommender systems (RS), which have been an essential part in a wide range of applications, can be formulated as a matrix completion (MC) problem. To boost the performance of MC, matrix completion with side information, called inductive matrix completion (IMC), was further proposed. In real applications, the factorized version of IMC is more favored due to its efficiency of optimization and implementation. Regarding the factorized version, traditional IMC method can be interpreted as learning an individual representation for each feature, which is independent from each other. Moreover, representations for the same features are shared across all users/items. However, the independent characteristic for features and shared characteristic for the same features across all users/items may limit the expressiveness of the model. The limitation also exists in variants of IMC, such as deep learning based IMC models. To break the limitation, we generalize recent advances of self-attention mechanism to IMC and propose a context-aware model called collaborative self-attention (CSA), which can jointly learn context-aware representations for features and perform inductive matrix completion process. Extensive experiments on three large-scale datasets from real RS applications demonstrate effectiveness of CSA.