Embracing Diffraction: A Paradigm Shift in Wireless Sensing and Communication

Wireless signals are integral to modern society, enabling both communication and increasingly, environmental sensing. While various propagation models exist, ranging from empirical methods to full-wave simulations, the phenomenon of electromagnetic diffraction is often treated as a secondary effect or a correction factor. This paper positions diffraction as a fundamentally important and underutilized mechanism that is rich with information about the physical environment. Specifically, diffraction-inducing elements generate distinct signatures that are rich with information about their underlying properties such as their geometries. We then argue that by understanding and exploiting these relationships, diffraction can be harnessed strategically. We introduce a general optimization framework to formalize this concept, illustrating how diffraction can be leveraged for both inverse problems (sensing scene details such as object geometries from measured fields) and forward problems (shaping RF fields for communication objectives by configuring diffracting elements). Focusing primarily on edge diffraction and Keller's Geometrical Theory of Diffraction (GTD), we discuss specific applications in RF sensing for scene understanding and in communications for RF field programming, drawing upon recent work. Overall, this paper lays out a vision for systematically incorporating diffraction into the design and operation of future wireless systems, paving the way for enhanced sensing capabilities and more robust communication strategies.

Crowd Size Estimation for Non-Uniform Spatial Distributions with mmWave Radar

Sensing with RF signals such as mmWave radar has gained considerable interest in recent years. This is particularly relevant to 6G networks, which aim to integrate sensing and communication (ISAC) capabilities for enhanced functionality. The contextual information provided by such sensing, whether collected by standalone non-ISAC units or integrated within ISAC, can not only optimize cellular network assets but can also serve as a valuable tool for a wide range of applications beyond network optimization. In this context, we present a novel methodology for crowd size estimation using monostatic mmWave radar, which is capable of accurately counting large crowds that are unevenly distributed across space. Our estimation approach relies on the rigorous derivation of occlusion probabilities, which are then used to mathematically characterize the probability distributions that describe the number of agents visible to the radar as a function of the crowd size. We then estimate the true crowd size by comparing these derived mathematical models to the empirical distribution of the number of visible agents detected by the radar. This method requires minimal sensing capabilities (e.g., angle-of-arrival information is not needed), thus being well suited for either a dedicated mmWave radar or an ISAC system. Extensive numerical simulations validate our methodology, demonstrating strong performance across diverse spatial distributions and for crowd sizes of up to (and including) 30 agents. We achieve a mean absolute error (MAE) of 0.48 agents, significantly outperforming a baseline which assumes that the agents are uniformly distributed in the area. Overall, our approach holds significant promise for a variety of applications including network resource allocation, crowd management, and urban planning.

Optimization of Mobile Robotic Relay Operation for Minimal Average Wait Time

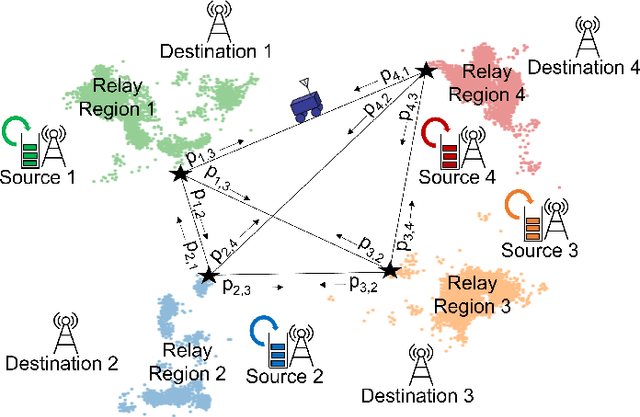
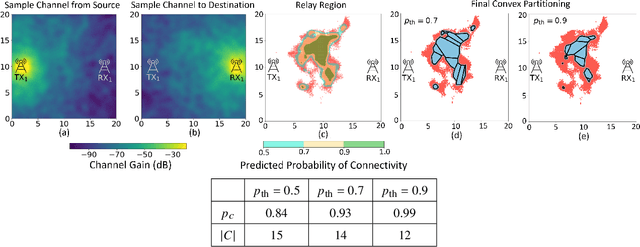
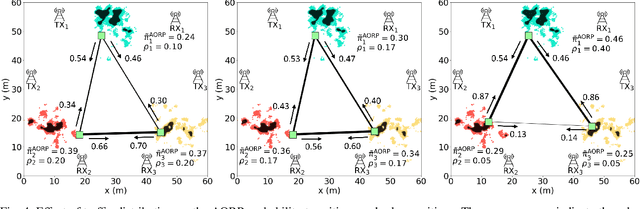
This paper considers trajectory planning for a mobile robot which persistently relays data between pairs of far-away communication nodes. Data accumulates stochastically at each source, and the robot must move to appropriate positions to enable data offload to the corresponding destination. The robot needs to minimize the average time that data waits at a source before being serviced. We are interested in finding optimal robotic routing policies consisting of 1) locations where the robot stops to relay (relay positions) and 2) conditional transition probabilities that determine the sequence in which the pairs are serviced. We first pose this problem as a non-convex problem that optimizes over both relay positions and transition probabilities. To find approximate solutions, we propose a novel algorithm which alternately optimizes relay positions and transition probabilities. For the former, we find efficient convex partitions of the non-convex relay regions, then formulate a mixed-integer second-order cone problem. For the latter, we find optimal transition probabilities via sequential least squares programming. We extensively analyze the proposed approach and mathematically characterize important system properties related to the robot's long-term energy consumption and service rate. Finally, through extensive simulation with real channel parameters, we verify the efficacy of our approach.