Split Conformal Prediction under Data Contamination

Conformal prediction is a non-parametric technique for constructing prediction intervals or sets from arbitrary predictive models under the assumption that the data is exchangeable. It is popular as it comes with theoretical guarantees on the marginal coverage of the prediction sets and the split conformal prediction variant has a very low computational cost compared to model training. We study the robustness of split conformal prediction in a data contamination setting, where we assume a small fraction of the calibration scores are drawn from a different distribution than the bulk. We quantify the impact of the corrupted data on the coverage and efficiency of the constructed sets when evaluated on "clean" test points, and verify our results with numerical experiments. Moreover, we propose an adjustment in the classification setting which we call Contamination Robust Conformal Prediction, and verify the efficacy of our approach using both synthetic and real datasets.

SteinGen: Generating Fidelitous and Diverse Graph Samples

Generating graphs that preserve characteristic structures while promoting sample diversity can be challenging, especially when the number of graph observations is small. Here, we tackle the problem of graph generation from only one observed graph. The classical approach of graph generation from parametric models relies on the estimation of parameters, which can be inconsistent or expensive to compute due to intractable normalisation constants. Generative modelling based on machine learning techniques to generate high-quality graph samples avoids parameter estimation but usually requires abundant training samples. Our proposed generating procedure, SteinGen, which is phrased in the setting of graphs as realisations of exponential random graph models, combines ideas from Stein's method and MCMC by employing Markovian dynamics which are based on a Stein operator for the target model. SteinGen uses the Glauber dynamics associated with an estimated Stein operator to generate a sample, and re-estimates the Stein operator from the sample after every sampling step. We show that on a class of exponential random graph models this novel "estimation and re-estimation" generation strategy yields high distributional similarity (high fidelity) to the original data, combined with high sample diversity.

Nonlinear Causal Discovery via Kernel Anchor Regression

Learning causal relationships is a fundamental problem in science. Anchor regression has been developed to address this problem for a large class of causal graphical models, though the relationships between the variables are assumed to be linear. In this work, we tackle the nonlinear setting by proposing kernel anchor regression (KAR). Beyond the natural formulation using a classic two-stage least square estimator, we also study an improved variant that involves nonparametric regression in three separate stages. We provide convergence results for the proposed KAR estimators and the identifiability conditions for KAR to learn the nonlinear structural equation models (SEM). Experimental results demonstrate the superior performances of the proposed KAR estimators over existing baselines.

On RKHS Choices for Assessing Graph Generators via Kernel Stein Statistics

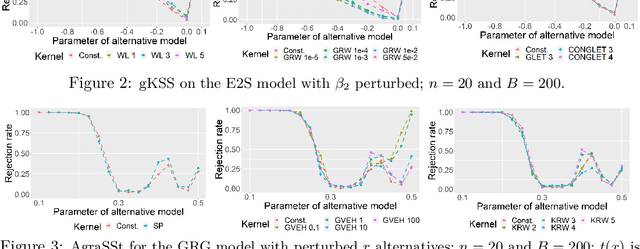
Score-based kernelised Stein discrepancy (KSD) tests have emerged as a powerful tool for the goodness of fit tests, especially in high dimensions; however, the test performance may depend on the choice of kernels in an underlying reproducing kernel Hilbert space (RKHS). Here we assess the effect of RKHS choice for KSD tests of random networks models, developed for exponential random graph models (ERGMs) in Xu and Reinert (2021)and for synthetic graph generators in Xu and Reinert (2022). We investigate the power performance and the computational runtime of the test in different scenarios, including both dense and sparse graph regimes. Experimental results on kernel performance for model assessment tasks are shown and discussed on synthetic and real-world network applications.

A Kernelised Stein Statistic for Assessing Implicit Generative Models

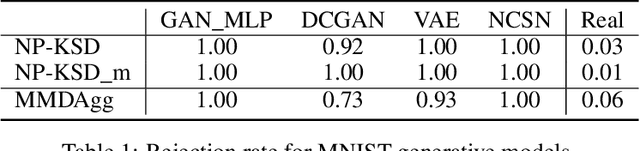
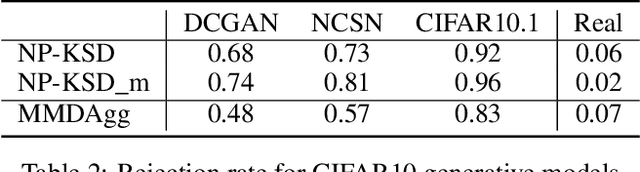
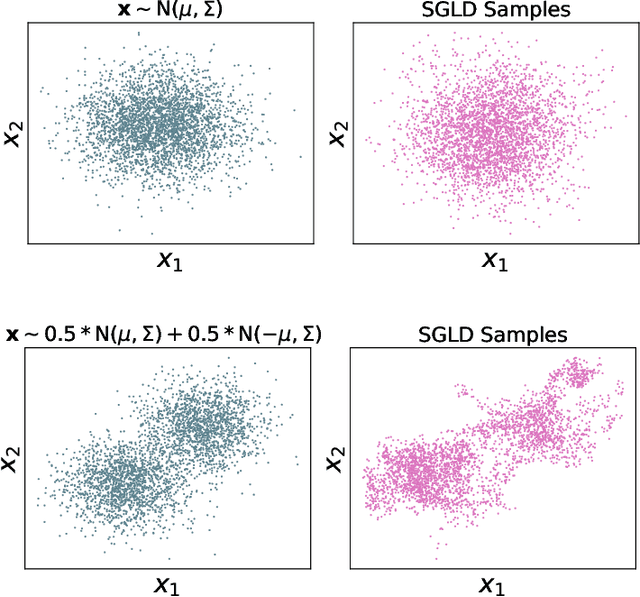
Synthetic data generation has become a key ingredient for training machine learning procedures, addressing tasks such as data augmentation, analysing privacy-sensitive data, or visualising representative samples. Assessing the quality of such synthetic data generators hence has to be addressed. As (deep) generative models for synthetic data often do not admit explicit probability distributions, classical statistical procedures for assessing model goodness-of-fit may not be applicable. In this paper, we propose a principled procedure to assess the quality of a synthetic data generator. The procedure is a kernelised Stein discrepancy (KSD)-type test which is based on a non-parametric Stein operator for the synthetic data generator of interest. This operator is estimated from samples which are obtained from the synthetic data generator and hence can be applied even when the model is only implicit. In contrast to classical testing, the sample size from the synthetic data generator can be as large as desired, while the size of the observed data, which the generator aims to emulate is fixed. Experimental results on synthetic distributions and trained generative models on synthetic and real datasets illustrate that the method shows improved power performance compared to existing approaches.

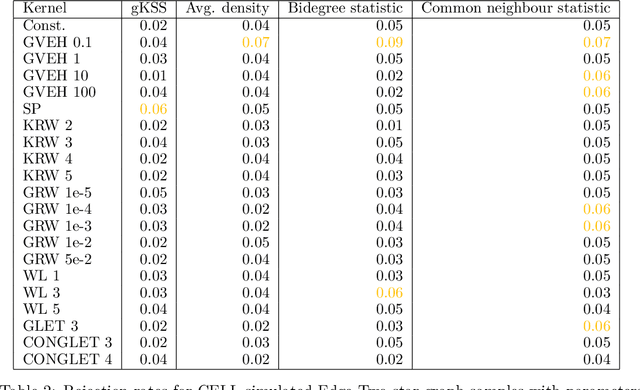
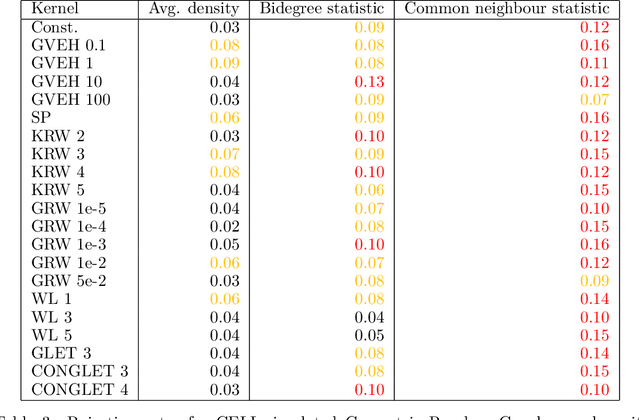
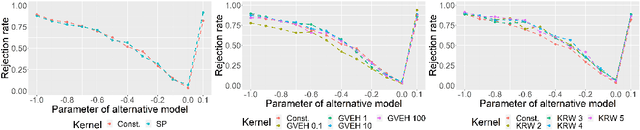
AgraSSt: Approximate Graph Stein Statistics for Interpretable Assessment of Implicit Graph Generators

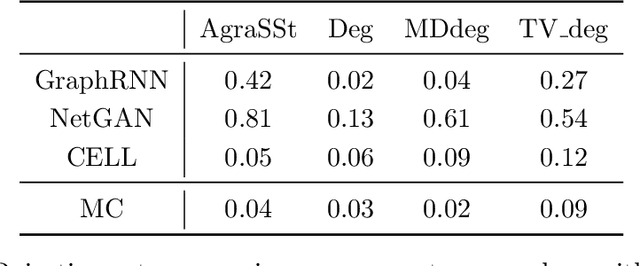
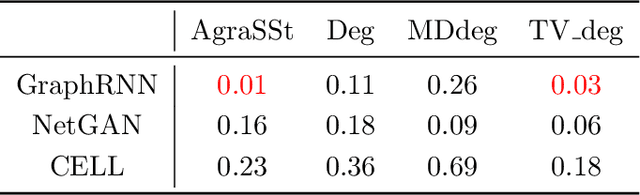
We propose and analyse a novel statistical procedure, coined AgraSSt, to assess the quality of graph generators that may not be available in explicit form. In particular, AgraSSt can be used to determine whether a learnt graph generating process is capable of generating graphs that resemble a given input graph. Inspired by Stein operators for random graphs, the key idea of AgraSSt is the construction of a kernel discrepancy based on an operator obtained from the graph generator. AgraSSt can provide interpretable criticisms for a graph generator training procedure and help identify reliable sample batches for downstream tasks. Using Stein`s method we give theoretical guarantees for a broad class of random graph models. We provide empirical results on both synthetic input graphs with known graph generation procedures, and real-world input graphs that the state-of-the-art (deep) generative models for graphs are trained on.

Generalised Kernel Stein Discrepancy(GKSD): A Unifying Approach for Non-parametric Goodness-of-fit Testing

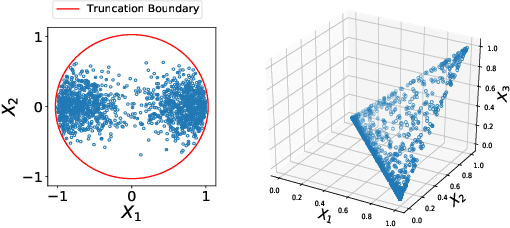
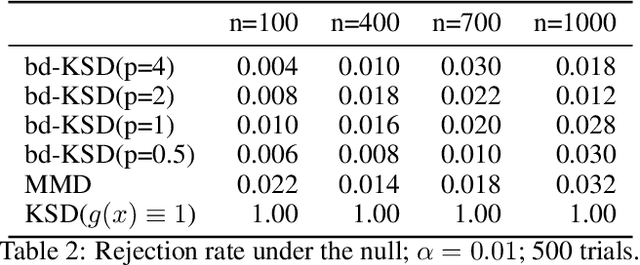
Non-parametric goodness-of-fit testing procedures based on kernel Stein discrepancies (KSD) are promising approaches to validate general unnormalised distributions in various scenarios. Existing works have focused on studying optimal kernel choices to boost test performances. However, the Stein operators are generally non-unique, while different choices of Stein operators can also have considerable effect on the test performances. In this work, we propose a unifying framework, the generalised kernel Stein discrepancy (GKSD), to theoretically compare and interpret different Stein operators in performing the KSD-based goodness-of-fit tests. We derive explicitly that how the proposed GKSD framework generalises existing Stein operators and their corresponding tests. In addition, we show thatGKSD framework can be used as a guide to develop kernel-based non-parametric goodness-of-fit tests for complex new data scenarios, e.g. truncated distributions or compositional data. Experimental results demonstrate that the proposed tests control type-I error well and achieve higher test power than existing approaches, including the test based on maximum-mean-discrepancy (MMD).

Meta Two-Sample Testing: Learning Kernels for Testing with Limited Data

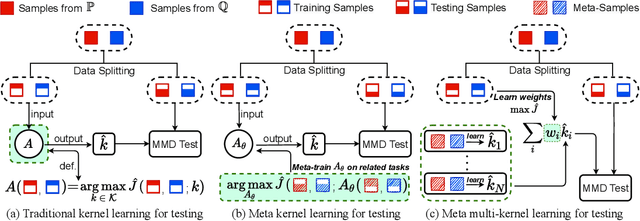
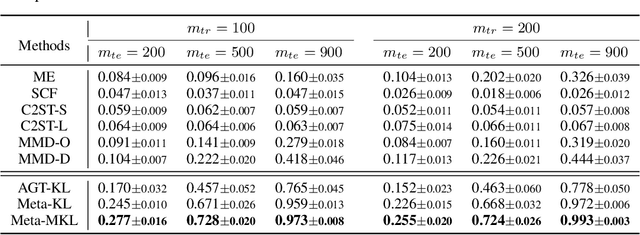
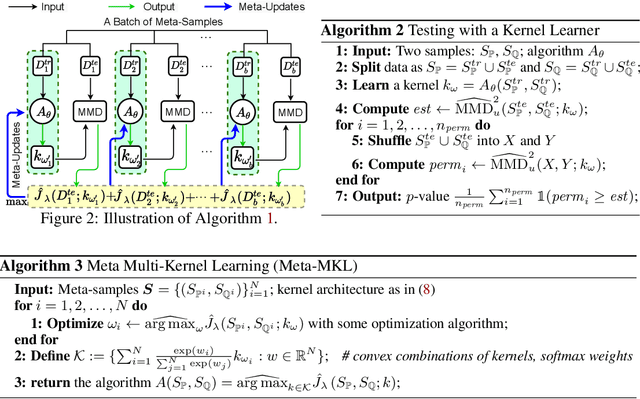
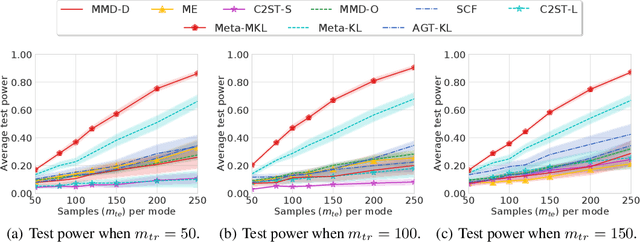
Modern kernel-based two-sample tests have shown great success in distinguishing complex, high-dimensional distributions with appropriate learned kernels. Previous work has demonstrated that this kernel learning procedure succeeds, assuming a considerable number of observed samples from each distribution. In realistic scenarios with very limited numbers of data samples, however, it can be challenging to identify a kernel powerful enough to distinguish complex distributions. We address this issue by introducing the problem of meta two-sample testing (M2ST), which aims to exploit (abundant) auxiliary data on related tasks to find an algorithm that can quickly identify a powerful test on new target tasks. We propose two specific algorithms for this task: a generic scheme which improves over baselines and amore tailored approach which performs even better. We provide both theoretical justification and empirical evidence that our proposed meta-testing schemes out-perform learning kernel-based tests directly from scarce observations, and identify when such schemes will be successful.

A Stein Goodness of fit Test for Exponential Random Graph Models

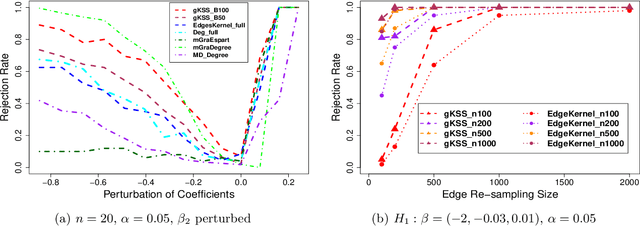
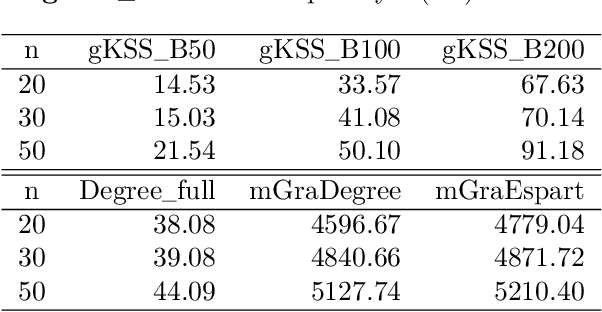
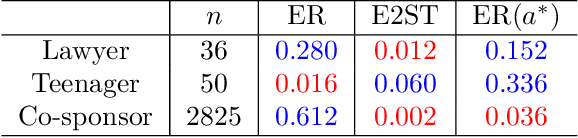
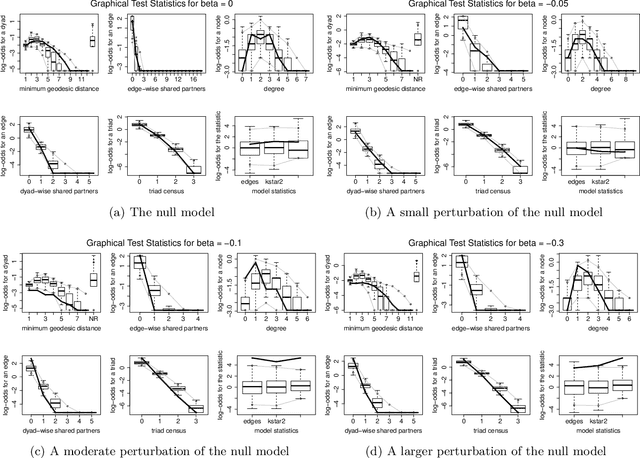
We propose and analyse a novel nonparametric goodness of fit testing procedure for exchangeable exponential random graph models (ERGMs) when a single network realisation is observed. The test determines how likely it is that the observation is generated from a target unnormalised ERGM density. Our test statistics are derived from a kernel Stein discrepancy, a divergence constructed via Steins method using functions in a reproducing kernel Hilbert space, combined with a discrete Stein operator for ERGMs. The test is a Monte Carlo test based on simulated networks from the target ERGM. We show theoretical properties for the testing procedure for a class of ERGMs. Simulation studies and real network applications are presented.

A kernel test for quasi-independence

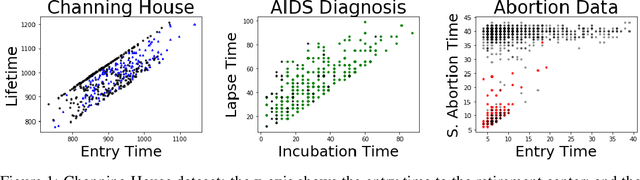
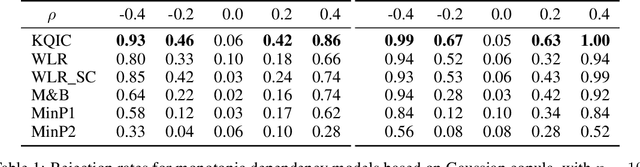
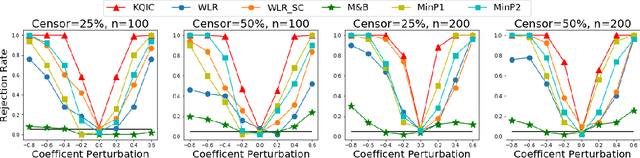
We consider settings in which the data of interest correspond to pairs of ordered times, e.g, the birth times of the first and second child, the times at which a new user creates an account and makes the first purchase on a website, and the entry and survival times of patients in a clinical trial. In these settings, the two times are not independent (the second occurs after the first), yet it is still of interest to determine whether there exists significant dependence {\em beyond} their ordering in time. We refer to this notion as "quasi-(in)dependence". For instance, in a clinical trial, to avoid biased selection, we might wish to verify that recruitment times are quasi-independent of survival times, where dependencies might arise due to seasonal effects. In this paper, we propose a nonparametric statistical test of quasi-independence. Our test considers a potentially infinite space of alternatives, making it suitable for complex data where the nature of the possible quasi-dependence is not known in advance. Standard parametric approaches are recovered as special cases, such as the classical conditional Kendall's tau, and log-rank tests. The tests apply in the right-censored setting: an essential feature in clinical trials, where patients can withdraw from the study. We provide an asymptotic analysis of our test-statistic, and demonstrate in experiments that our test obtains better power than existing approaches, while being more computationally efficient.