Random Tree Model of Meaningful Memory

Traditional studies of memory for meaningful narratives focus on specific stories and their semantic structures but do not address common quantitative features of recall across different narratives. We introduce a statistical ensemble of random trees to represent narratives as hierarchies of key points, where each node is a compressed representation of its descendant leaves, which are the original narrative segments. Recall is modeled as constrained by working memory capacity from this hierarchical structure. Our analytical solution aligns with observations from large-scale narrative recall experiments. Specifically, our model explains that (1) average recall length increases sublinearly with narrative length, and (2) individuals summarize increasingly longer narrative segments in each recall sentence. Additionally, the theory predicts that for sufficiently long narratives, a universal, scale-invariant limit emerges, where the fraction of a narrative summarized by a single recall sentence follows a distribution independent of narrative length.

Hierarchical Working Memory and a New Magic Number

The extremely limited working memory span, typically around four items, contrasts sharply with our everyday experience of processing much larger streams of sensory information concurrently. This disparity suggests that working memory can organize information into compact representations such as chunks, yet the underlying neural mechanisms remain largely unknown. Here, we propose a recurrent neural network model for chunking within the framework of the synaptic theory of working memory. We showed that by selectively suppressing groups of stimuli, the network can maintain and retrieve the stimuli in chunks, hence exceeding the basic capacity. Moreover, we show that our model can dynamically construct hierarchical representations within working memory through hierarchical chunking. A consequence of this proposed mechanism is a new limit on the number of items that can be stored and subsequently retrieved from working memory, depending only on the basic working memory capacity when chunking is not invoked. Predictions from our model were confirmed by analyzing single-unit responses in epileptic patients and memory experiments with verbal material. Our work provides a novel conceptual and analytical framework for understanding the on-the-fly organization of information in the brain that is crucial for cognition.

Advantage of Quantum Neural Networks as Quantum Information Decoders

A promising strategy to protect quantum information from noise-induced errors is to encode it into the low-energy states of a topological quantum memory device. However, readout errors from such memory under realistic settings is less understood. We study the problem of decoding quantum information encoded in the groundspaces of topological stabilizer Hamiltonians in the presence of generic perturbations, such as quenched disorder. We first prove that the standard stabilizer-based error correction and decoding schemes work adequately well in such perturbed quantum codes by showing that the decoding error diminishes exponentially in the distance of the underlying unperturbed code. We then prove that Quantum Neural Network (QNN) decoders provide an almost quadratic improvement on the readout error. Thus, we demonstrate provable advantage of using QNNs for decoding realistic quantum error-correcting codes, and our result enables the exploration of a wider range of non-stabilizer codes in the near-term laboratory settings.

Non-equilibrium physics: from spin glasses to machine and neural learning

Disordered many-body systems exhibit a wide range of emergent phenomena across different scales. These complex behaviors can be utilized for various information processing tasks such as error correction, learning, and optimization. Despite the empirical success of utilizing these systems for intelligent tasks, the underlying principles that govern their emergent intelligent behaviors remain largely unknown. In this thesis, we aim to characterize such emergent intelligence in disordered systems through statistical physics. We chart a roadmap for our efforts in this thesis based on two axes: learning mechanisms (long-term memory vs. working memory) and learning dynamics (artificial vs. natural). Throughout our journey, we uncover relationships between learning mechanisms and physical dynamics that could serve as guiding principles for designing intelligent systems. We hope that our investigation into the emergent intelligence of seemingly disparate learning systems can expand our current understanding of intelligence beyond neural systems and uncover a wider range of computational substrates suitable for AI applications.

Many-body localized hidden Born machine

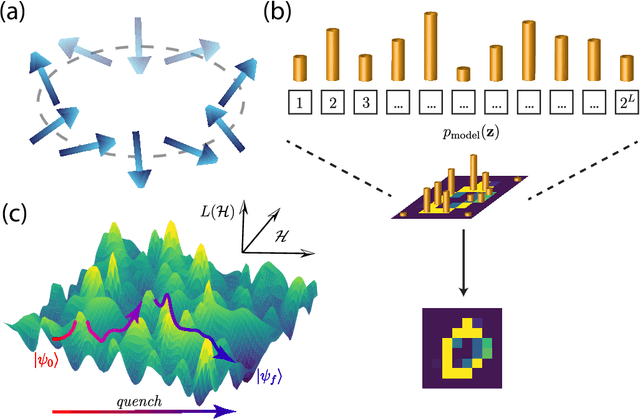
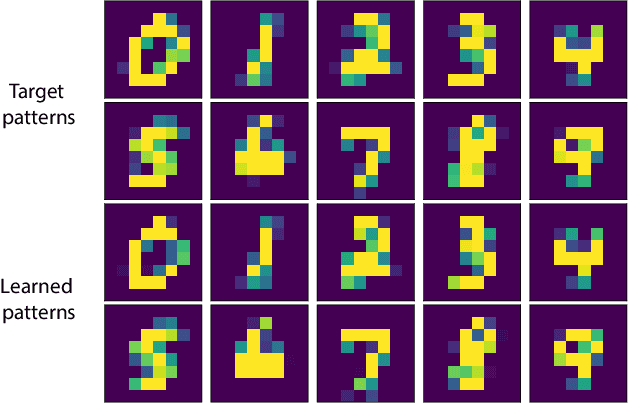
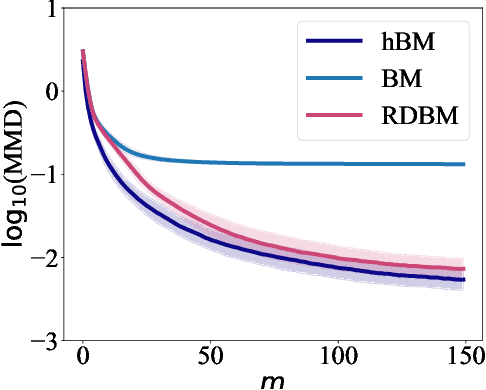
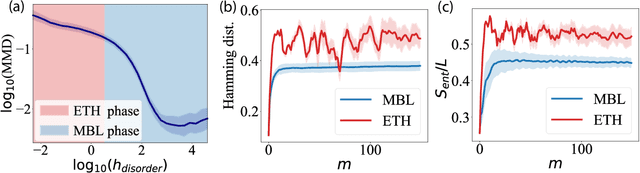
Born Machines are quantum-inspired generative models that leverage the probabilistic nature of quantum states. Here, we present a new architecture called many-body localized (MBL) hidden Born machine that uses both MBL dynamics and hidden units as learning resources. We theoretically prove that MBL Born machines possess more expressive power than classical models, and the introduction of hidden units boosts its learning power. We numerically demonstrate that the MBL hidden Born machine is capable of learning a toy dataset consisting of patterns of MNIST handwritten digits, quantum data obtained from quantum many-body states, and non-local parity data. In order to understand the mechanism behind learning, we track physical quantities such as von Neumann entanglement entropy and Hamming distance during learning, and compare the learning outcomes in the MBL, thermal, and Anderson localized phases. We show that the superior learning power of the MBL phase relies importantly on both localization and interaction. Our architecture and algorithm provide novel strategies of utilizing quantum many-body systems as learning resources, and reveal a powerful connection between disorder, interaction, and learning in quantum systems.

A theory of learning with constrained weight-distribution

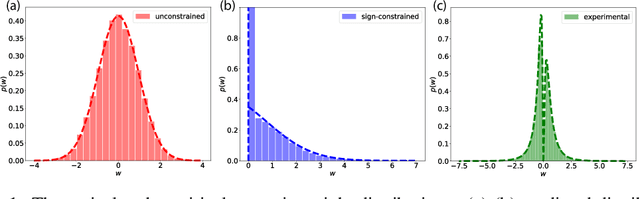
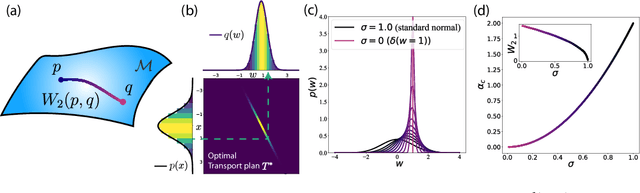
A central question in computational neuroscience is how structure determines function in neural networks. The emerging high-quality large-scale connectomic datasets raise the question of what general functional principles can be gleaned from structural information such as the distribution of excitatory/inhibitory synapse types and the distribution of synaptic weights. Motivated by this question, we developed a statistical mechanical theory of learning in neural networks that incorporates structural information as constraints. We derived an analytical solution for the memory capacity of the perceptron, a basic feedforward model of supervised learning, with constraint on the distribution of its weights. Our theory predicts that the reduction in capacity due to the constrained weight-distribution is related to the Wasserstein distance between the imposed distribution and that of the standard normal distribution. To test the theoretical predictions, we use optimal transport theory and information geometry to develop an SGD-based algorithm to find weights that simultaneously learn the input-output task and satisfy the distribution constraint. We show that training in our algorithm can be interpreted as geodesic flows in the Wasserstein space of probability distributions. We further developed a statistical mechanical theory for teacher-student perceptron rule learning and ask for the best way for the student to incorporate prior knowledge of the rule. Our theory shows that it is beneficial for the learner to adopt different prior weight distributions during learning, and shows that distribution-constrained learning outperforms unconstrained and sign-constrained learning. Our theory and algorithm provide novel strategies for incorporating prior knowledge about weights into learning, and reveal a powerful connection between structure and function in neural networks.

A Closer Look at Disentangling in $β$-VAE

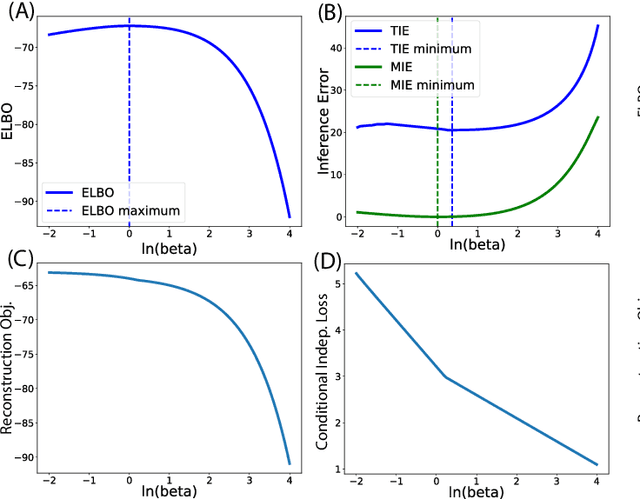
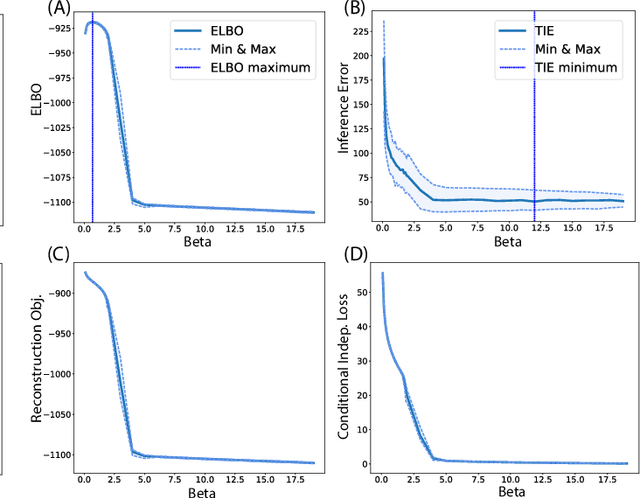
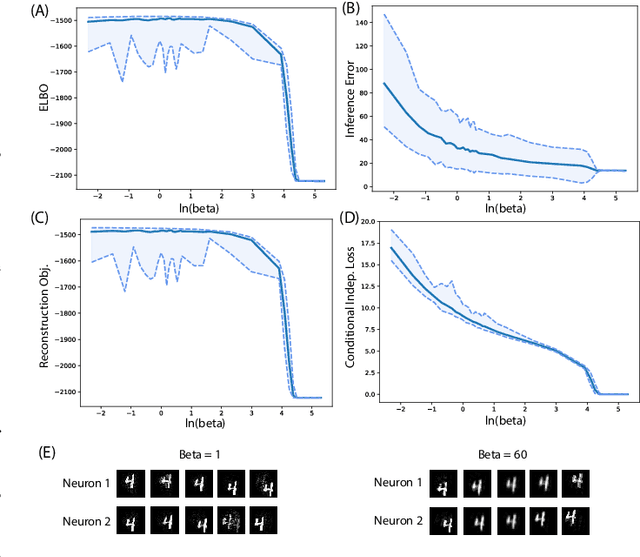
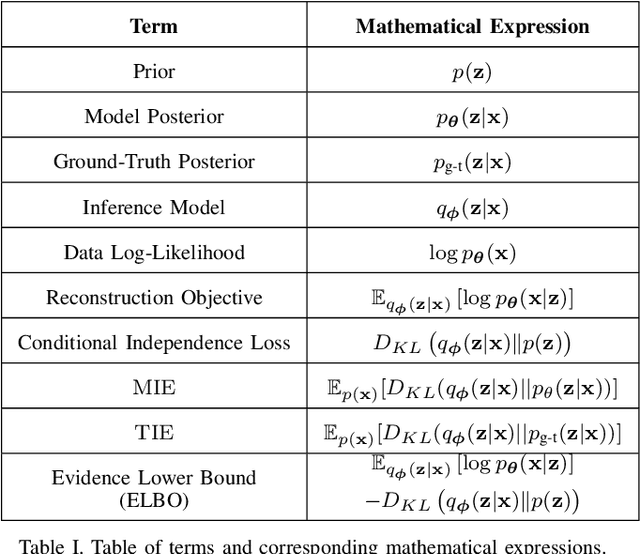
In many data analysis tasks, it is beneficial to learn representations where each dimension is statistically independent and thus disentangled from the others. If data generating factors are also statistically independent, disentangled representations can be formed by Bayesian inference of latent variables. We examine a generalization of the Variational Autoencoder (VAE), $\beta$-VAE, for learning such representations using variational inference. $\beta$-VAE enforces conditional independence of its bottleneck neurons controlled by its hyperparameter $\beta$. This condition is in general not compatible with the statistical independence of latents. By providing analytical and numerical arguments, we show that this incompatibility leads to a non-monotonic inference performance in $\beta$-VAE with a finite optimal $\beta$.