Optimal Estimation of Change in a Population of Parameters

Paired estimation of change in parameters of interest over a population plays a central role in several application domains including those in the social sciences, epidemiology, medicine and biology. In these domains, the size of the population under study is often very large, however, the number of observations available per individual in the population is very small (\emph{sparse observations}) which makes the problem challenging. Consider the setting with $N$ independent individuals, each with unknown parameters $(p_i, q_i)$ drawn from some unknown distribution on $[0, 1]^2$. We observe $X_i \sim \text{Bin}(t, p_i)$ before an event and $Y_i \sim \text{Bin}(t, q_i)$ after the event. Provided these paired observations, $\{(X_i, Y_i) \}_{i=1}^N$, our goal is to accurately estimate the \emph{distribution of the change in parameters}, $\delta_i := q_i - p_i$, over the population and properties of interest like the \emph{$\ell_1$-magnitude of the change} with sparse observations ($t\ll N$). We provide \emph{information theoretic lower bounds} on the error in estimating the distribution of change and the $\ell_1$-magnitude of change. Furthermore, we show that the following two step procedure achieves the optimal error bounds: first, estimate the full joint distribution of the paired parameters using the maximum likelihood estimator (MLE) and then estimate the distribution of change and the $\ell_1$-magnitude of change using the joint MLE. Notably, and perhaps surprisingly, these error bounds are of the same order as the minimax optimal error bounds for learning the \emph{full} joint distribution itself (in Wasserstein-1 distance); in other words, estimating the magnitude of the change of parameters over the population is, in a minimax sense, as difficult as estimating the full joint distribution itself.

Maximum Likelihood Estimation for Learning Populations of Parameters

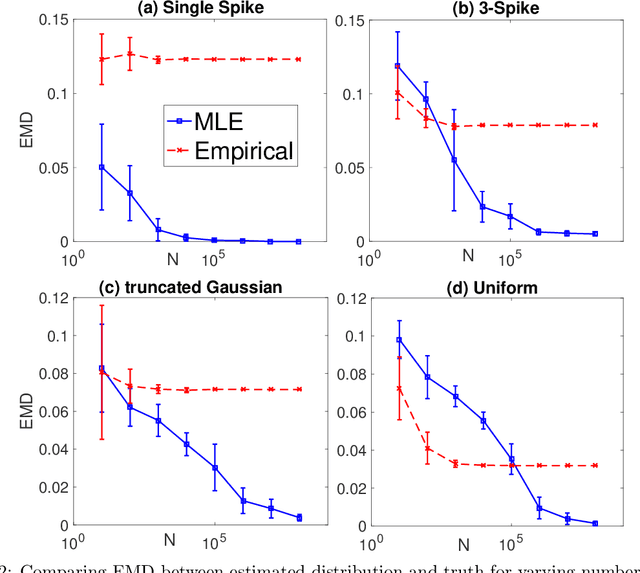
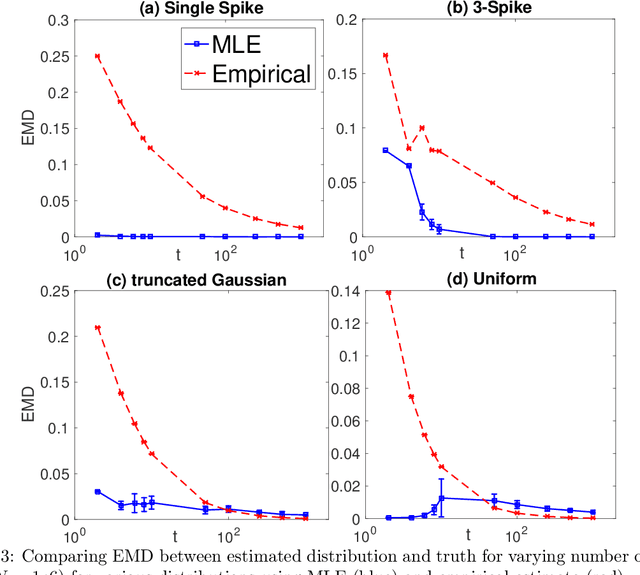
Consider a setting with $N$ independent individuals, each with an unknown parameter, $p_i \in [0, 1]$ drawn from some unknown distribution $P^\star$. After observing the outcomes of $t$ independent Bernoulli trials, i.e., $X_i \sim \text{Binomial}(t, p_i)$ per individual, our objective is to accurately estimate $P^\star$. This problem arises in numerous domains, including the social sciences, psychology, health-care, and biology, where the size of the population under study is usually large while the number of observations per individual is often limited. Our main result shows that, in the regime where $t \ll N$, the maximum likelihood estimator (MLE) is both statistically minimax optimal and efficiently computable. Precisely, for sufficiently large $N$, the MLE achieves the information theoretic optimal error bound of $\mathcal{O}(\frac{1}{t})$ for $t < c\log{N}$, with regards to the earth mover's distance (between the estimated and true distributions). More generally, in an exponentially large interval of $t$ beyond $c \log{N}$, the MLE achieves the minimax error bound of $\mathcal{O}(\frac{1}{\sqrt{t\log N}})$. In contrast, regardless of how large $N$ is, the naive "plug-in" estimator for this problem only achieves the sub-optimal error of $\Theta(\frac{1}{\sqrt{t}})$.

Efficient Algorithms and Lower Bounds for Robust Linear Regression

We study the problem of high-dimensional linear regression in a robust model where an $\epsilon$-fraction of the samples can be adversarially corrupted. We focus on the fundamental setting where the covariates of the uncorrupted samples are drawn from a Gaussian distribution $\mathcal{N}(0, \Sigma)$ on $\mathbb{R}^d$. We give nearly tight upper bounds and computational lower bounds for this problem. Specifically, our main contributions are as follows: For the case that the covariance matrix is known to be the identity, we give a sample near-optimal and computationally efficient algorithm that outputs a candidate hypothesis vector $\widehat{\beta}$ which approximates the unknown regression vector $\beta$ within $\ell_2$-norm $O(\epsilon \log(1/\epsilon) \sigma)$, where $\sigma$ is the standard deviation of the random observation noise. An error of $\Omega (\epsilon \sigma)$ is information-theoretically necessary, even with infinite sample size. Prior work gave an algorithm for this problem with sample complexity $\tilde{\Omega}(d^2/\epsilon^2)$ whose error guarantee scales with the $\ell_2$-norm of $\beta$. For the case of unknown covariance, we show that we can efficiently achieve the same error guarantee as in the known covariance case using an additional $\tilde{O}(d^2/\epsilon^2)$ unlabeled examples. On the other hand, an error of $O(\epsilon \sigma)$ can be information-theoretically attained with $O(d/\epsilon^2)$ samples. We prove a Statistical Query (SQ) lower bound providing evidence that this quadratic tradeoff in the sample size is inherent. More specifically, we show that any polynomial time SQ learning algorithm for robust linear regression (in Huber's contamination model) with estimation complexity $O(d^{2-c})$, where $c>0$ is an arbitrarily small constant, must incur an error of $\Omega(\sqrt{\epsilon} \sigma)$.

Estimating Learnability in the Sublinear Data Regime

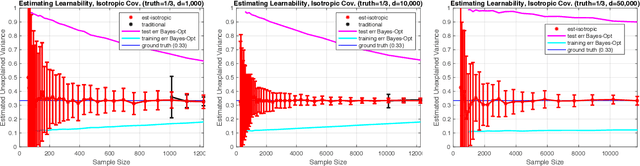
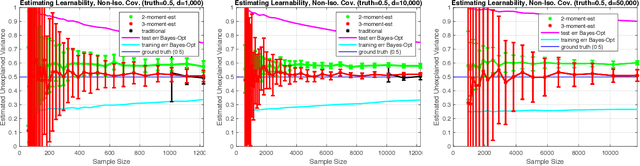
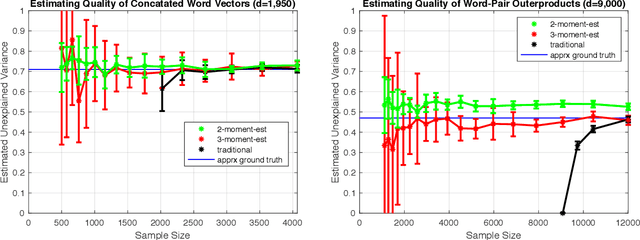
We consider the problem of estimating how well a model class is capable of fitting a distribution of labeled data. We show that it is often possible to accurately estimate this "learnability" even when given an amount of data that is too small to reliably learn any accurate model. Our first result applies to the setting where the data is drawn from a $d$-dimensional distribution with isotropic covariance, and the label of each datapoint is an arbitrary noisy function of the datapoint. In this setting, we show that with $O(\sqrt{d})$ samples, one can accurately estimate the fraction of the variance of the label that can be explained via the best linear function of the data. We extend these techniques to the setting of binary classification, where we show that in an analogous setting, the prediction error of the best linear classifier can be accurately estimated given $O(\sqrt{d})$ labeled samples. Note that in both the linear regression and binary classification settings, even if there is no noise in the labels, a sample size linear in the dimension, $d$, is required to \emph{learn} any function correlated with the underlying model. We further extend our estimation approach to the setting where the data distribution has an (unknown) arbitrary covariance matrix, allowing these techniques to be applied to settings where the model class consists of a linear function applied to a nonlinear embedding of the data. Finally, we demonstrate the practical viability of these approaches on synthetic and real data. This ability to estimate the explanatory value of a set of features (or dataset), even in the regime in which there is too little data to realize that explanatory value, may be relevant to the scientific and industrial settings for which data collection is expensive and there are many potentially relevant feature sets that could be collected.

Recovering Structured Probability Matrices

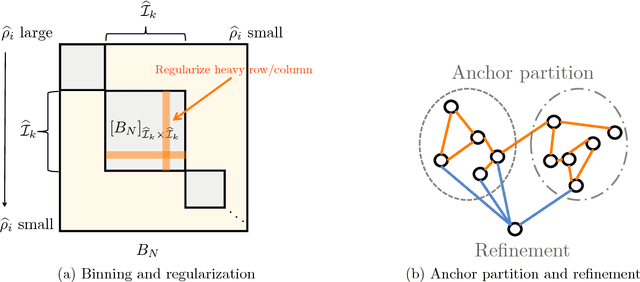
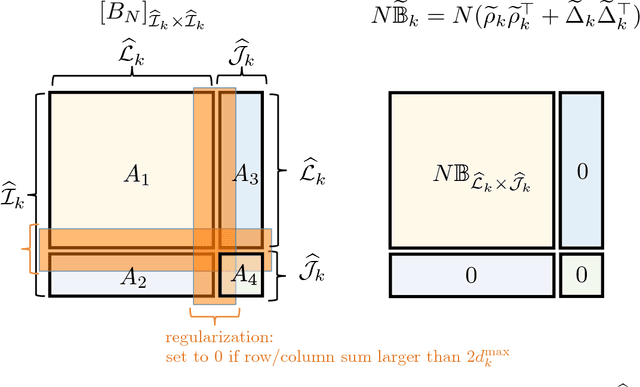
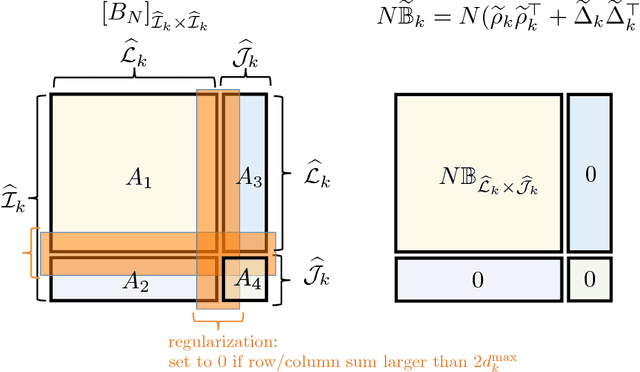
We consider the problem of accurately recovering a matrix B of size M by M , which represents a probability distribution over M2 outcomes, given access to an observed matrix of "counts" generated by taking independent samples from the distribution B. How can structural properties of the underlying matrix B be leveraged to yield computationally efficient and information theoretically optimal reconstruction algorithms? When can accurate reconstruction be accomplished in the sparse data regime? This basic problem lies at the core of a number of questions that are currently being considered by different communities, including building recommendation systems and collaborative filtering in the sparse data regime, community detection in sparse random graphs, learning structured models such as topic models or hidden Markov models, and the efforts from the natural language processing community to compute "word embeddings". Our results apply to the setting where B has a low rank structure. For this setting, we propose an efficient algorithm that accurately recovers the underlying M by M matrix using Theta(M) samples. This result easily translates to Theta(M) sample algorithms for learning topic models and learning hidden Markov Models. These linear sample complexities are optimal, up to constant factors, in an extremely strong sense: even testing basic properties of the underlying matrix (such as whether it has rank 1 or 2) requires Omega(M) samples. We provide an even stronger lower bound where distinguishing whether a sequence of observations were drawn from the uniform distribution over M observations versus being generated by an HMM with two hidden states requires Omega(M) observations. This precludes sublinear-sample hypothesis tests for basic properties, such as identity or uniformity, as well as sublinear sample estimators for quantities such as the entropy rate of HMMs.

Learning Populations of Parameters

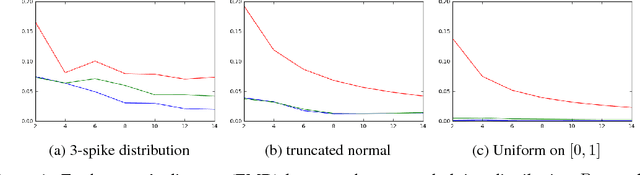
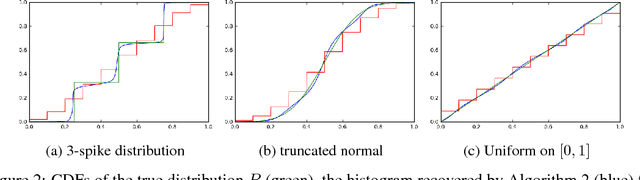
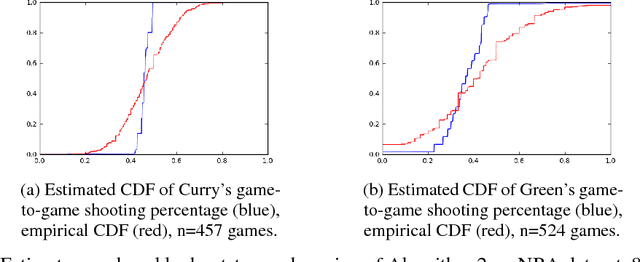
Consider the following estimation problem: there are $n$ entities, each with an unknown parameter $p_i \in [0,1]$, and we observe $n$ independent random variables, $X_1,\ldots,X_n$, with $X_i \sim $ Binomial$(t, p_i)$. How accurately can one recover the "histogram" (i.e. cumulative density function) of the $p_i$'s? While the empirical estimates would recover the histogram to earth mover distance $\Theta(\frac{1}{\sqrt{t}})$ (equivalently, $\ell_1$ distance between the CDFs), we show that, provided $n$ is sufficiently large, we can achieve error $O(\frac{1}{t})$ which is information theoretically optimal. We also extend our results to the multi-dimensional parameter case, capturing settings where each member of the population has multiple associated parameters. Beyond the theoretical results, we demonstrate that the recovery algorithm performs well in practice on a variety of datasets, providing illuminating insights into several domains, including politics, sports analytics, and variation in the gender ratio of offspring.

Spectrum Estimation from Samples

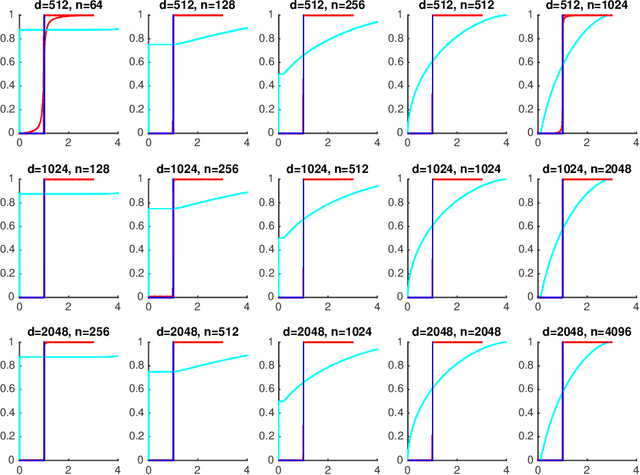
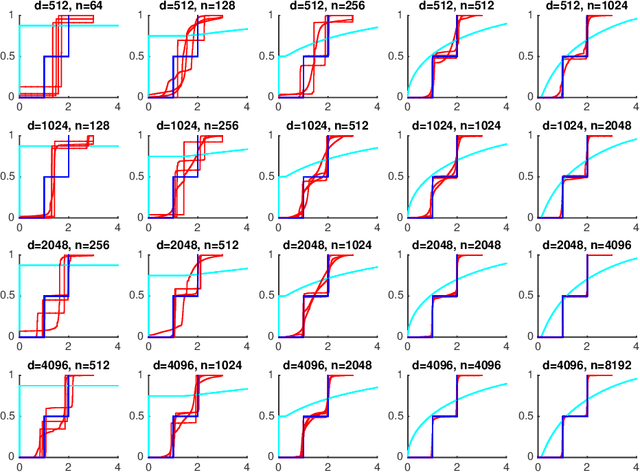
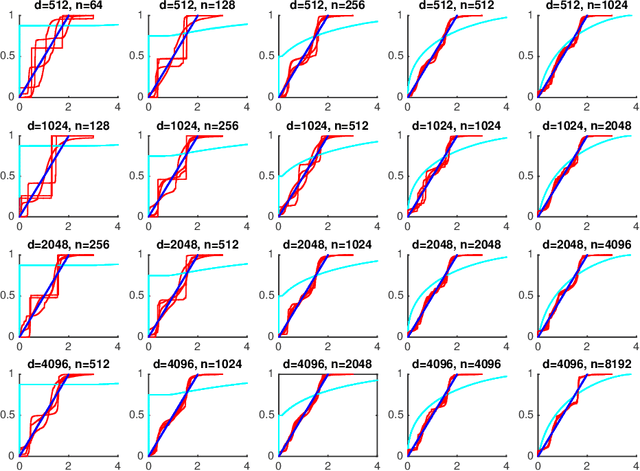
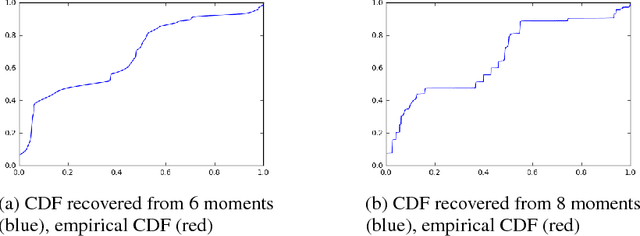
We consider the problem of approximating the set of eigenvalues of the covariance matrix of a multivariate distribution (equivalently, the problem of approximating the "population spectrum"), given access to samples drawn from the distribution. The eigenvalues of the covariance of a distribution contain basic information about the distribution, including the presence or lack of structure in the distribution, the effective dimensionality of the distribution, and the applicability of higher-level machine learning and multivariate statistical tools. We consider this fundamental recovery problem in the regime where the number of samples is comparable, or even sublinear in the dimensionality of the distribution in question. First, we propose a theoretically optimal and computationally efficient algorithm for recovering the moments of the eigenvalues of the population covariance matrix. We then leverage this accurate moment recovery, via a Wasserstein distance argument, to show that the vector of eigenvalues can be accurately recovered. We provide finite--sample bounds on the expected error of the recovered eigenvalues, which imply that our estimator is asymptotically consistent as the dimensionality of the distribution and sample size tend towards infinity, even in the sublinear sample regime where the ratio of the sample size to the dimensionality tends to zero. In addition to our theoretical results, we show that our approach performs well in practice for a broad range of distributions and sample sizes.