Low-discrepancy Sampling in the Expanded Dimensional Space: An Acceleration Technique for Particle Swarm Optimization

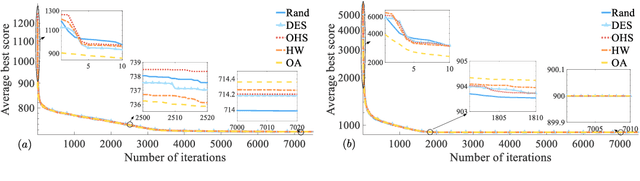
Compared with random sampling, low-discrepancy sampling is more effective in covering the search space. However, the existing research cannot definitely state whether the impact of a low-discrepancy sample on particle swarm optimization (PSO) is positive or negative. Using Niderreiter's theorem, this study completes an error analysis of PSO, which reveals that the error bound of PSO at each iteration depends on the dispersion of the sample set in an expanded dimensional space. Based on this error analysis, an acceleration technique for PSO-type algorithms is proposed with low-discrepancy sampling in the expanded dimensional space. The acceleration technique can generate a low-discrepancy sample set with a smaller dispersion, compared with a random sampling, in the expanded dimensional space; it also reduces the error at each iteration, and hence improves the convergence speed. The acceleration technique is combined with the standard PSO and the comprehensive learning particle swarm optimization, and the performance of the improved algorithm is compared with the original algorithm. The experimental results show that the two improved algorithms have significantly faster convergence speed under the same accuracy requirement.

Updating velocities in heterogeneous comprehensive learning particle swarm optimization with low-discrepancy sequences

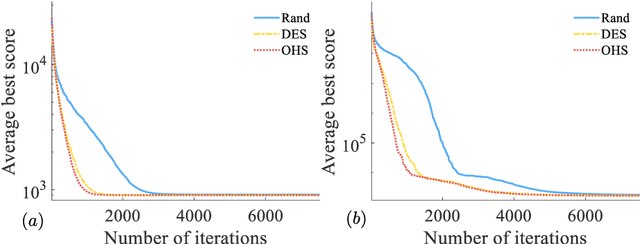
Heterogeneous comprehensive learning particle swarm optimization (HCLPSO) is a type of evolutionary algorithm with enhanced exploration and exploitation capabilities. The low-discrepancy sequence (LDS) is more uniform in covering the search space than random sequences. In this paper, making use of the good uniformity of LDS to improve HCLPSO is researched. Numerical experiments are performed to show that it is impossible to effectively improve the search ability of HCLPSO by only using LDS to generate the initial population. However, if we properly choose some random sequences from the HCLPSO velocities updating formula and replace them with the deterministic LDS, we can obtain a more efficient algorithm. Compared with the original HCLPSO under the same accuracy requirement, the HCLPSO updating the velocities with the deterministic LDS can significantly reduce the iterations required for finding the optimal solution, without decreasing the success rate.