Primal-dual algorithm for contextual stochastic combinatorial optimization

This paper introduces a novel approach to contextual stochastic optimization, integrating operations research and machine learning to address decision-making under uncertainty. Traditional methods often fail to leverage contextual information, which underscores the necessity for new algorithms. In this study, we utilize neural networks with combinatorial optimization layers to encode policies. Our goal is to minimize the empirical risk, which is estimated from past data on uncertain parameters and contexts. To that end, we present a surrogate learning problem and a generic primal-dual algorithm that is applicable to various combinatorial settings in stochastic optimization. Our approach extends classic Fenchel-Young loss results and introduces a new regularization method using sparse perturbations on the distribution simplex. This allows for tractable updates in the original space and can accommodate diverse objective functions. We demonstrate the linear convergence of our algorithm under certain conditions and provide a bound on the non-optimality of the resulting policy in terms of the empirical risk. Experiments on a contextual stochastic minimum weight spanning tree problem show that our algorithm is efficient and scalable, achieving performance comparable to imitation learning of solutions computed using an expensive Lagrangian-based heuristic.

Efficient Smoothed Concomitant Lasso Estimation for High Dimensional Regression

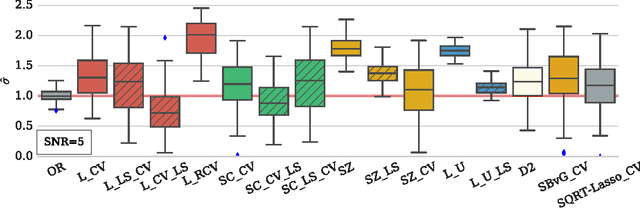
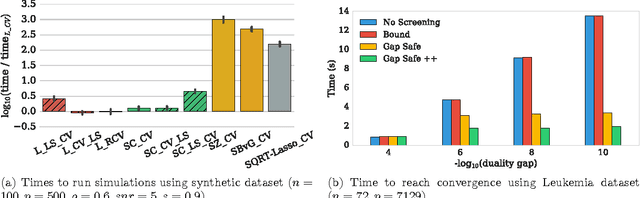
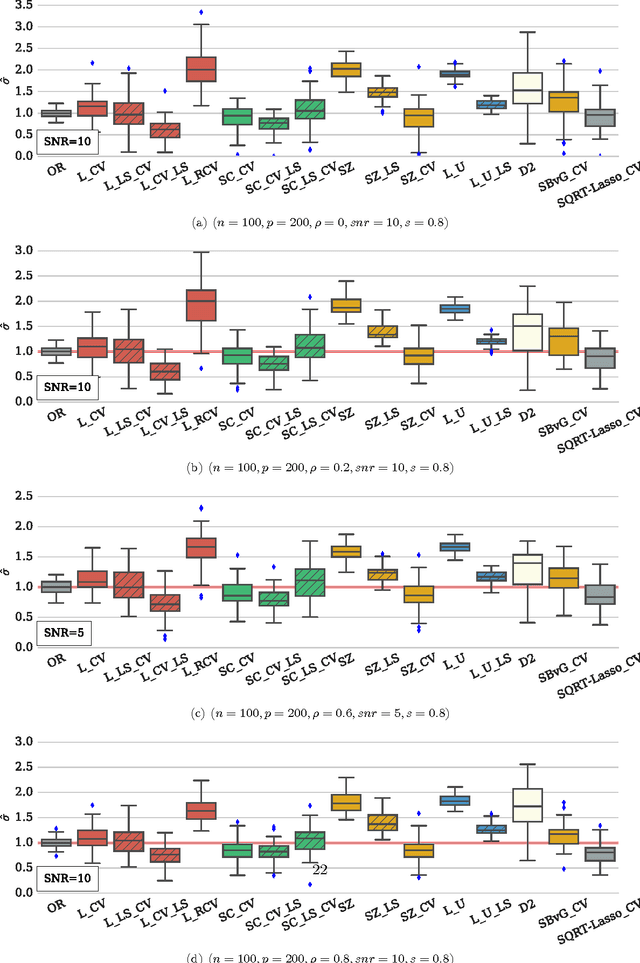
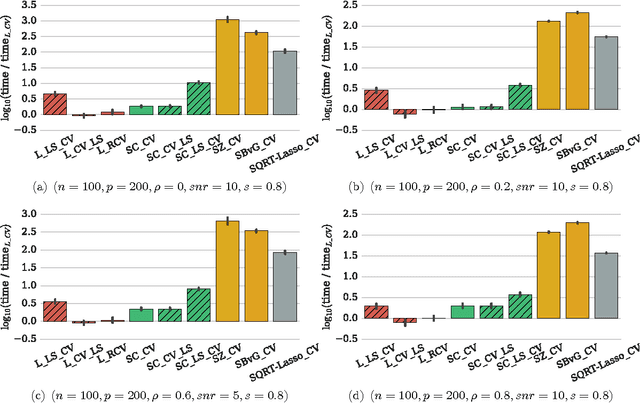
In high dimensional settings, sparse structures are crucial for efficiency, both in term of memory, computation and performance. It is customary to consider $\ell_1$ penalty to enforce sparsity in such scenarios. Sparsity enforcing methods, the Lasso being a canonical example, are popular candidates to address high dimension. For efficiency, they rely on tuning a parameter trading data fitting versus sparsity. For the Lasso theory to hold this tuning parameter should be proportional to the noise level, yet the latter is often unknown in practice. A possible remedy is to jointly optimize over the regression parameter as well as over the noise level. This has been considered under several names in the literature: Scaled-Lasso, Square-root Lasso, Concomitant Lasso estimation for instance, and could be of interest for confidence sets or uncertainty quantification. In this work, after illustrating numerical difficulties for the Smoothed Concomitant Lasso formulation, we propose a modification we coined Smoothed Concomitant Lasso, aimed at increasing numerical stability. We propose an efficient and accurate solver leading to a computational cost no more expansive than the one for the Lasso. We leverage on standard ingredients behind the success of fast Lasso solvers: a coordinate descent algorithm, combined with safe screening rules to achieve speed efficiency, by eliminating early irrelevant features.