Primal-dual algorithm for contextual stochastic combinatorial optimization

This paper introduces a novel approach to contextual stochastic optimization, integrating operations research and machine learning to address decision-making under uncertainty. Traditional methods often fail to leverage contextual information, which underscores the necessity for new algorithms. In this study, we utilize neural networks with combinatorial optimization layers to encode policies. Our goal is to minimize the empirical risk, which is estimated from past data on uncertain parameters and contexts. To that end, we present a surrogate learning problem and a generic primal-dual algorithm that is applicable to various combinatorial settings in stochastic optimization. Our approach extends classic Fenchel-Young loss results and introduces a new regularization method using sparse perturbations on the distribution simplex. This allows for tractable updates in the original space and can accommodate diverse objective functions. We demonstrate the linear convergence of our algorithm under certain conditions and provide a bound on the non-optimality of the resulting policy in terms of the empirical risk. Experiments on a contextual stochastic minimum weight spanning tree problem show that our algorithm is efficient and scalable, achieving performance comparable to imitation learning of solutions computed using an expensive Lagrangian-based heuristic.

Learning with Combinatorial Optimization Layers: a Probabilistic Approach

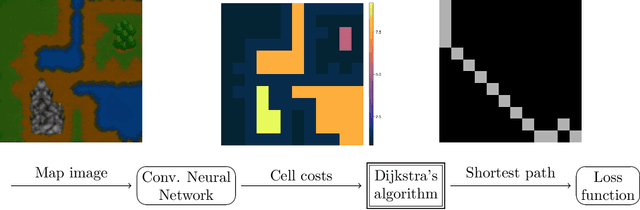
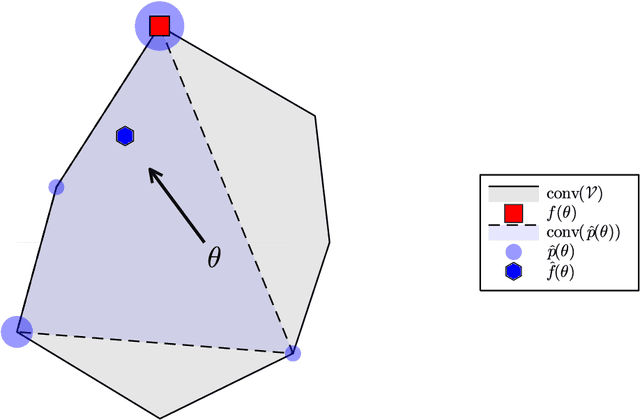
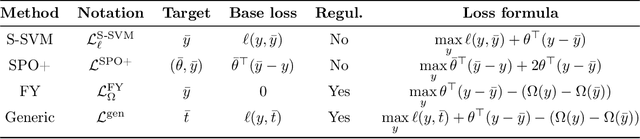
Combinatorial optimization (CO) layers in machine learning (ML) pipelines are a powerful tool to tackle data-driven decision tasks, but they come with two main challenges. First, the solution of a CO problem often behaves as a piecewise constant function of its objective parameters. Given that ML pipelines are typically trained using stochastic gradient descent, the absence of slope information is very detrimental. Second, standard ML losses do not work well in combinatorial settings. A growing body of research addresses these challenges through diverse methods. Unfortunately, the lack of well-maintained implementations slows down the adoption of CO layers. In this paper, building upon previous works, we introduce a probabilistic perspective on CO layers, which lends itself naturally to approximate differentiation and the construction of structured losses. We recover many approaches from the literature as special cases, and we also derive new ones. Based on this unifying perspective, we present InferOpt.jl, an open-source Julia package that 1) allows turning any CO oracle with a linear objective into a differentiable layer, and 2) defines adequate losses to train pipelines containing such layers. Our library works with arbitrary optimization algorithms, and it is fully compatible with Julia's ML ecosystem. We demonstrate its abilities using a pathfinding problem on video game maps.