Input-sensitive dense-sparse primitive compositions for GNN acceleration

Graph neural networks (GNN) have become an important class of neural network models that have gained popularity in domains such as social and financial network analysis. Different phases of GNN computations can be modeled using both dense and sparse matrix operations. There have been many frameworks and optimization techniques proposed in the literature to accelerate GNNs. However, getting consistently high performance across many input graphs with different sparsity patterns and GNN embedding sizes has remained difficult. In this paper, we propose different algebraic reassociations of GNN computations that lead to novel dense and sparse matrix primitive selections and compositions. We show that the profitability of these compositions depends on the input graph, embedding size, and the target hardware. We developed SENSEi, a system that uses a data-driven adaptive strategy to select the best composition given the input graph and GNN embedding sizes. Our evaluations on a wide range of graphs and embedding sizes show that SENSEi achieves geomean speedups of $1.105\times$ (up to $2.959\times$) and $1.187\times$ (up to $1.99\times$) on graph convolutional networks and geomean speedups of $2.307\times$ (up to $35.866\times$) and $1.44\times$ (up to $5.69\times$) on graph attention networks on CPUs and GPUs respectively over the widely used Deep Graph Library. Further, we show that the compositions yield notable synergistic performance benefits on top of other established sparse optimizations such as sparse matrix tiling by evaluating against a well-tuned baseline.

Accelerating Genetic Programming using GPUs

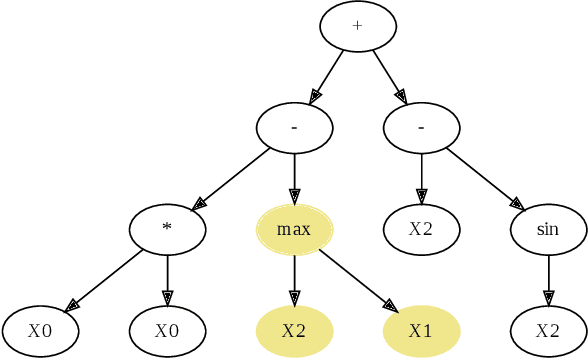
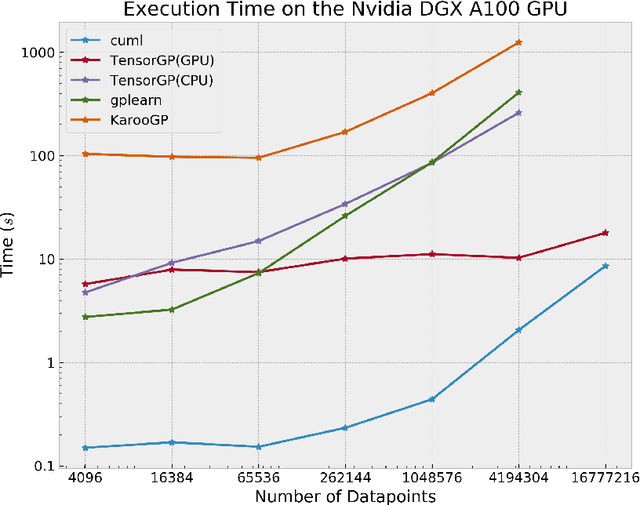
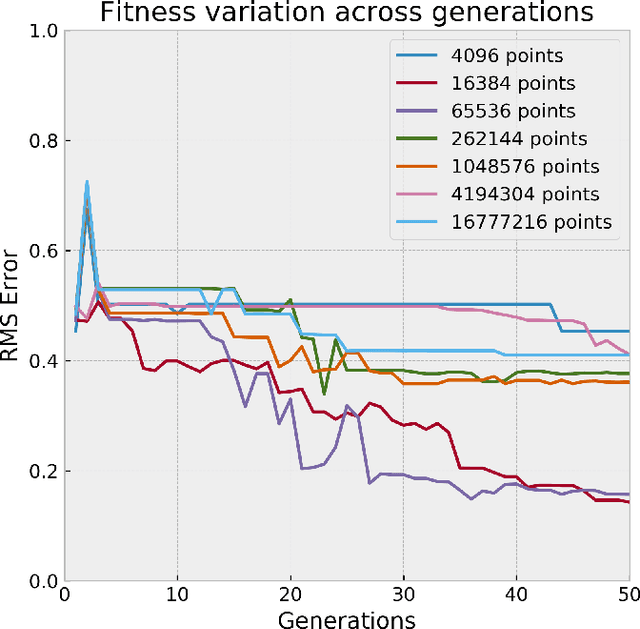
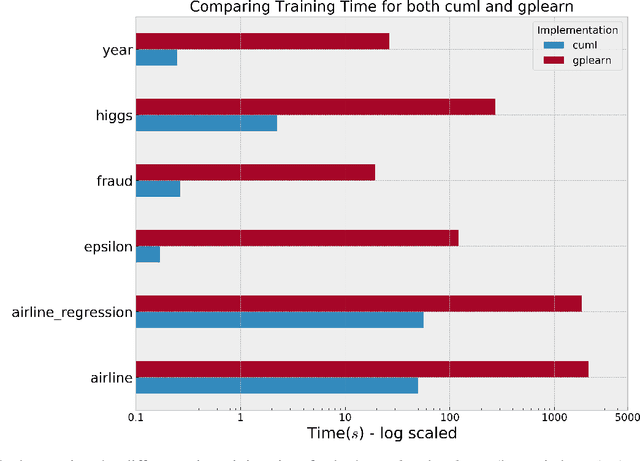
Genetic Programming (GP), an evolutionary learning technique, has multiple applications in machine learning such as curve fitting, data modelling, feature selection, classification etc. GP has several inherent parallel steps, making it an ideal candidate for GPU based parallelization. This paper describes a GPU accelerated stack-based variant of the generational GP algorithm which can be used for symbolic regression and binary classification. The selection and evaluation steps of the generational GP algorithm are parallelized using CUDA. We introduce representing candidate solution expressions as prefix lists, which enables evaluation using a fixed-length stack in GPU memory. CUDA based matrix vector operations are also used for computation of the fitness of population programs. We evaluate our algorithm on synthetic datasets for the Pagie Polynomial (ranging in size from $4096$ to $16$ million points), profiling training times of our algorithm with other standard symbolic regression libraries viz. gplearn, TensorGP and KarooGP. In addition, using $6$ large-scale regression and classification datasets usually used for comparing gradient boosting algorithms, we run performance benchmarks on our algorithm and gplearn, profiling the training time, test accuracy, and loss. On an NVIDIA DGX-A100 GPU, our algorithm outperforms all the previously listed frameworks, and in particular, achieves average speedups of $119\times$ and $40\times$ against gplearn on the synthetic and large scale datasets respectively.