Veronika Strnadova-Neeley
Geodesic Learning via Unsupervised Decision Forests
Jul 05, 2019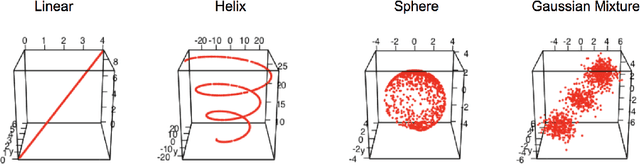
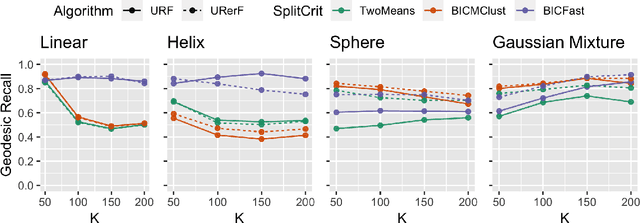
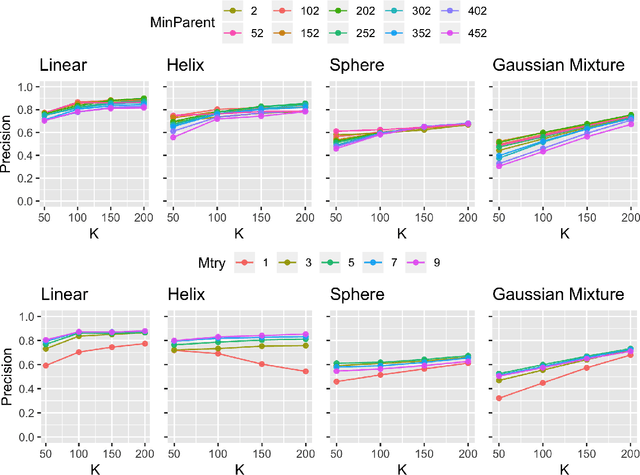
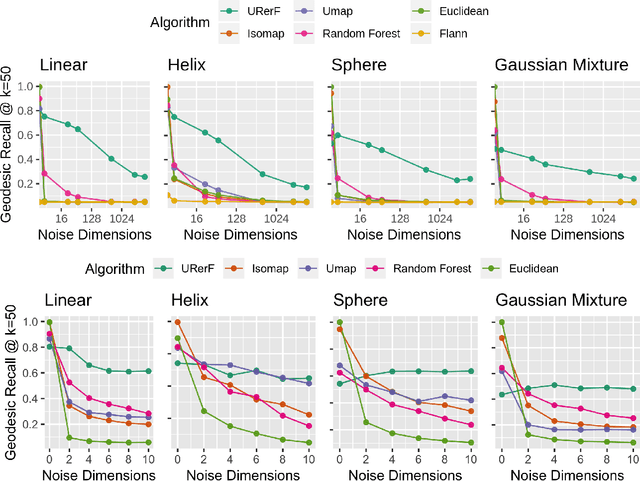
Abstract:Geodesic distance is the shortest path between two points in a Riemannian manifold. Manifold learning algorithms, such as Isomap, seek to learn a manifold that preserves geodesic distances. However, such methods operate on the ambient dimensionality, and are therefore fragile to noise dimensions. We developed an unsupervised random forest method (URerF) to approximately learn geodesic distances in linear and nonlinear manifolds with noise. URerF operates on low-dimensional sparse linear combinations of features, rather than the full observed dimensionality. To choose the optimal split in a computationally efficient fashion, we developed a fast Bayesian Information Criterion statistic for Gaussian mixture models. We introduce geodesic precision-recall curves which quantify performance relative to the true latent manifold. Empirical results on simulated and real data demonstrate that URerF is robust to high-dimensional noise, where as other methods, such as Isomap, UMAP, and FLANN, quickly deteriorate in such settings. In particular, URerF is able to estimate geodesic distances on a real connectome dataset better than other approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge