Vasilis Syrgkanis
Adversarial Estimation of Riesz Representers
Dec 30, 2020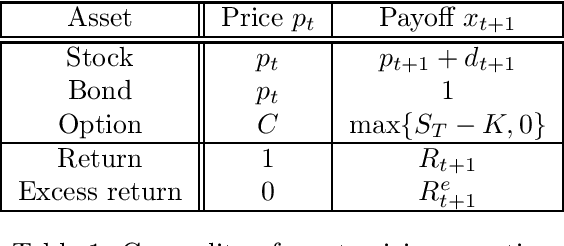
Abstract:We provide an adversarial approach to estimating Riesz representers of linear functionals within arbitrary function spaces. We prove oracle inequalities based on the localized Rademacher complexity of the function space used to approximate the Riesz representer and the approximation error. These inequalities imply fast finite sample mean-squared-error rates for many function spaces of interest, such as high-dimensional sparse linear functions, neural networks and reproducing kernel Hilbert spaces. Our approach offers a new way of estimating Riesz representers with a plethora of recently introduced machine learning techniques. We show how our estimator can be used in the context of de-biasing structural/causal parameters in semi-parametric models, for automated orthogonalization of moment equations and for estimating the stochastic discount factor in the context of asset pricing.
Asymptotics of the Empirical Bootstrap Method Beyond Asymptotic Normality
Nov 23, 2020Abstract:One of the most commonly used methods for forming confidence intervals for statistical inference is the empirical bootstrap, which is especially expedient when the limiting distribution of the estimator is unknown. However, despite its ubiquitous role, its theoretical properties are still not well understood for non-asymptotically normal estimators. In this paper, under stability conditions, we establish the limiting distribution of the empirical bootstrap estimator, derive tight conditions for it to be asymptotically consistent, and quantify the speed of convergence. Moreover, we propose three alternative ways to use the bootstrap method to build confidence intervals with coverage guarantees. Finally, we illustrate the generality and tightness of our results by a series of examples, including uniform confidence bands, two-sample kernel tests, minmax stochastic programs and the empirical risk of stacked estimators.
Bid Prediction in Repeated Auctions with Learning
Jul 26, 2020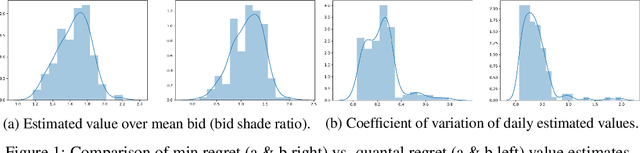
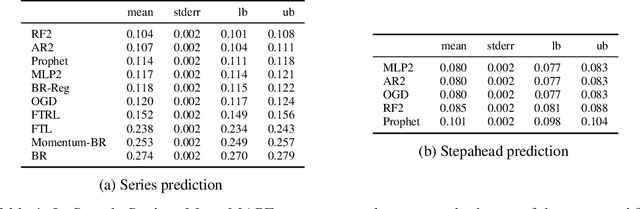
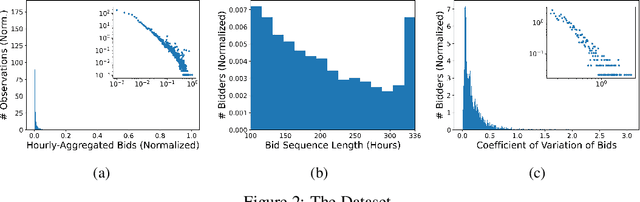
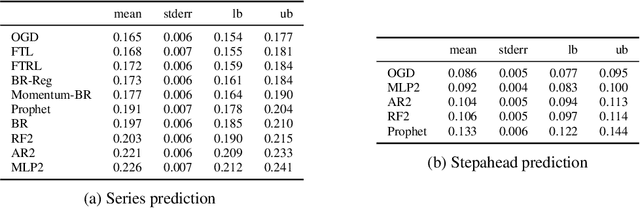
Abstract:We consider the problem of bid prediction in repeated auctions and evaluate the performance of econometric methods for learning agents using a dataset from a mainstream sponsored search auction marketplace. Sponsored search auctions is a billion dollar industry and the main source of revenue of several tech giants. A critical problem in optimizing such marketplaces is understanding how bidders will react to changes in the auction design. We propose the use of no-regret based econometrics for bid prediction, modelling players as no-regret learners with respect to a utility function, unknown to the analyst. We apply these methods in a real-world dataset from the BingAds sponsored search auction marketplace and show that no-regret econometric methods perform comparable to state-of-the-art time-series machine learning methods when there is no co-variate shift, but significantly out-perform machine learning methods when there is a co-variate shift between the training and test periods. This portrays the importance of using structural econometric approaches in predicting how players will respond to changes in the market. Moreover, we show that among structural econometric methods, approaches based on no-regret learning out-perform more traditional, equilibrium-based, econometric methods that assume that players continuously best-respond to competition.
Minimax Estimation of Conditional Moment Models
Jun 12, 2020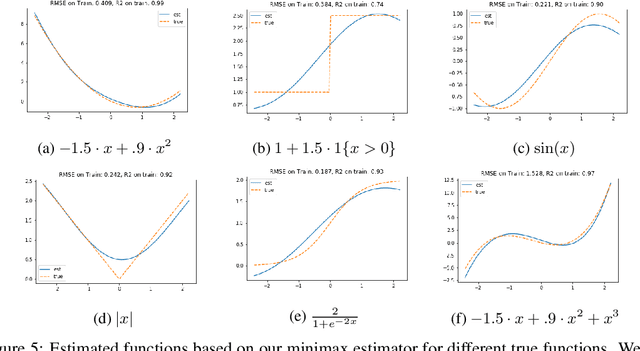
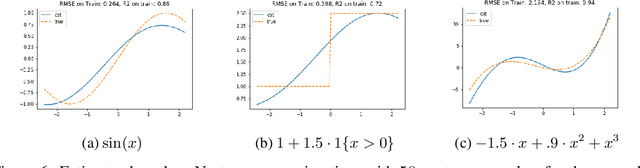
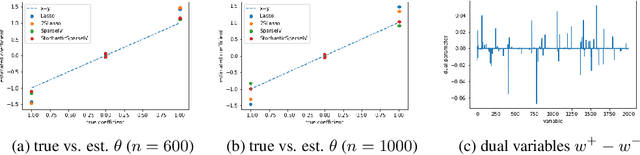
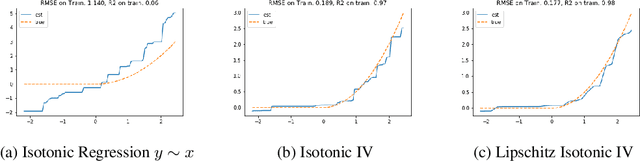
Abstract:We develop an approach for estimating models described via conditional moment restrictions, with a prototypical application being non-parametric instrumental variable regression. We introduce a min-max criterion function, under which the estimation problem can be thought of as solving a zero-sum game between a modeler who is optimizing over the hypothesis space of the target model and an adversary who identifies violating moments over a test function space. We analyze the statistical estimation rate of the resulting estimator for arbitrary hypothesis spaces, with respect to an appropriate analogue of the mean squared error metric, for ill-posed inverse problems. We show that when the minimax criterion is regularized with a second moment penalty on the test function and the test function space is sufficiently rich, then the estimation rate scales with the critical radius of the hypothesis and test function spaces, a quantity which typically gives tight fast rates. Our main result follows from a novel localized Rademacher analysis of statistical learning problems defined via minimax objectives. We provide applications of our main results for several hypothesis spaces used in practice such as: reproducing kernel Hilbert spaces, high dimensional sparse linear functions, spaces defined via shape constraints, ensemble estimators such as random forests, and neural networks. For each of these applications we provide computationally efficient optimization methods for solving the corresponding minimax problem (e.g. stochastic first-order heuristics for neural networks). In several applications, we show how our modified mean squared error rate, combined with conditions that bound the ill-posedness of the inverse problem, lead to mean squared error rates. We conclude with an extensive experimental analysis of the proposed methods.
Double/Debiased Machine Learning for Dynamic Treatment Effects
Feb 17, 2020
Abstract:We consider the estimation of treatment effects in settings when multiple treatments are assigned over time and treatments can have a causal effect on future outcomes. We formulate the problem as a linear state space Markov process with a high dimensional state and propose an extension of the double/debiased machine learning framework to estimate the dynamic effects of treatments. Our method allows the use of arbitrary machine learning methods to control for the high dimensional state, subject to a mean square error guarantee, while still allowing parametric estimation and construction of confidence intervals for the dynamic treatment effect parameters of interest. Our method is based on a sequential regression peeling process, which we show can be equivalently interpreted as a Neyman orthogonal moment estimator. This allows us to show root-n asymptotic normality of the estimated causal effects.
Machine Learning Estimation of Heterogeneous Treatment Effects with Instruments
Jun 06, 2019
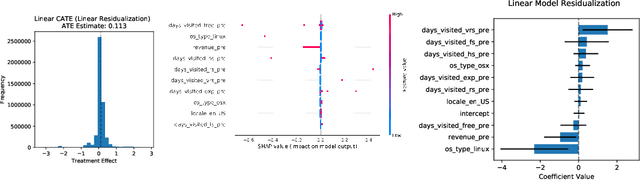
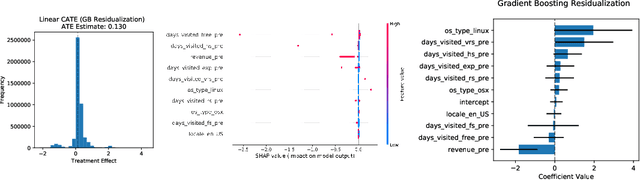
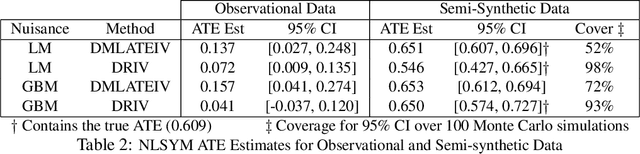
Abstract:We consider the estimation of heterogeneous treatment effects with arbitrary machine learning methods in the presence of unobserved confounders with the aid of a valid instrument. Such settings arise in A/B tests with an intent-to-treat structure, where the experimenter randomizes over which user will receive a recommendation to take an action, and we are interested in the effect of the downstream action. We develop a statistical learning approach to the estimation of heterogeneous effects, reducing the problem to the minimization of an appropriate loss function that depends on a set of auxiliary models (each corresponding to a separate prediction task). The reduction enables the use of all recent algorithmic advances (e.g. neural nets, forests). We show that the estimated effect model is robust to estimation errors in the auxiliary models, by showing that the loss satisfies a Neyman orthogonality criterion. Our approach can be used to estimate projections of the true effect model on simpler hypothesis spaces. When these spaces are parametric, then the parameter estimates are asymptotically normal, which enables construction of confidence sets. We applied our method to estimate the effect of membership on downstream webpage engagement on TripAdvisor, using as an instrument an intent-to-treat A/B test among 4 million TripAdvisor users, where some users received an easier membership sign-up process. We also validate our method on synthetic data and on public datasets for the effects of schooling on income.
Semi-Parametric Efficient Policy Learning with Continuous Actions
May 24, 2019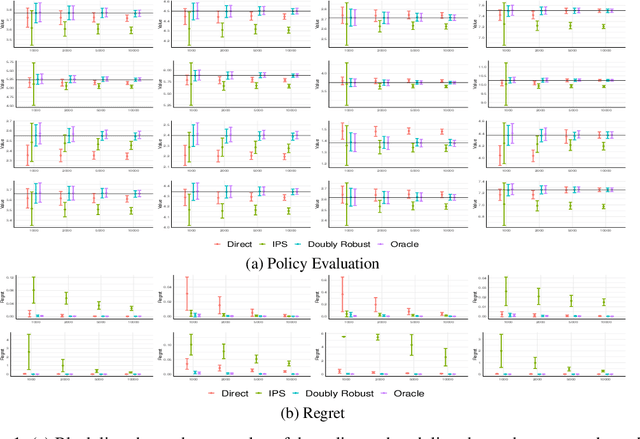
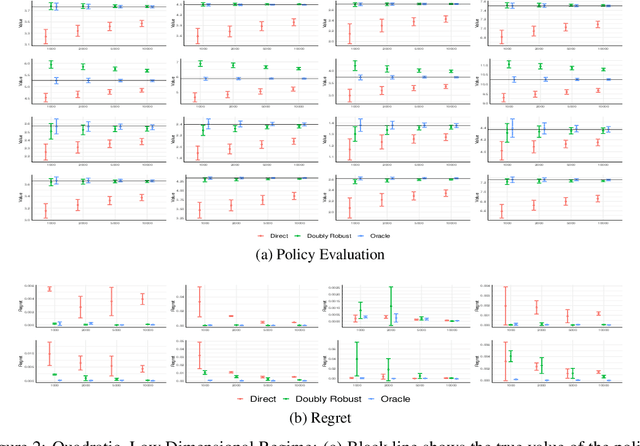
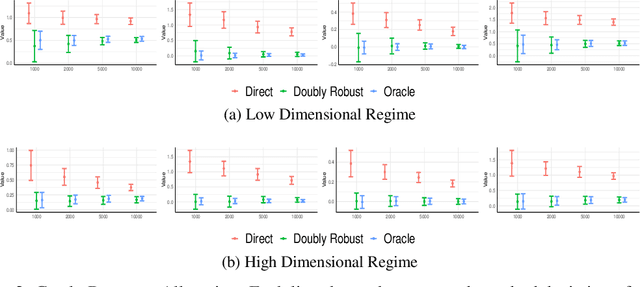
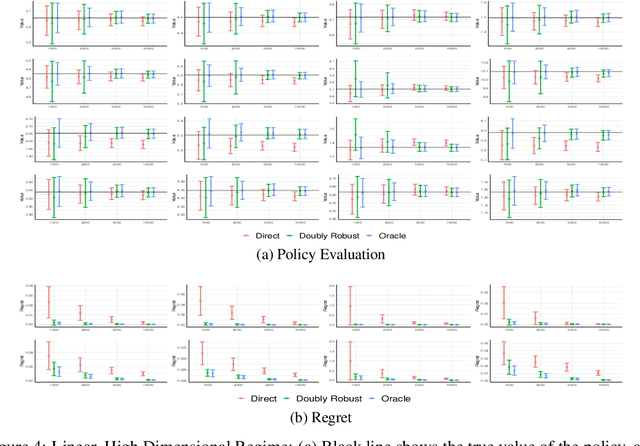
Abstract:We consider off-policy evaluation and optimization with continuous action spaces. We focus on observational data where the data collection policy is unknown and needs to be estimated. We take a semi-parametric approach where the value function takes a known parametric form in the treatment, but we are agnostic on how it depends on the observed contexts. We propose a doubly robust off-policy estimate for this setting and show that off-policy optimization based on this estimate is robust to estimation errors of the policy function or the regression model. Our results also apply if the model does not satisfy our semi-parametric form, but rather we measure regret in terms of the best projection of the true value function to this functional space. Our work extends prior approaches of policy optimization from observational data that only considered discrete actions. We provide an experimental evaluation of our method in a synthetic data example motivated by optimal personalized pricing and costly resource allocation.
Orthogonal Statistical Learning
Jan 25, 2019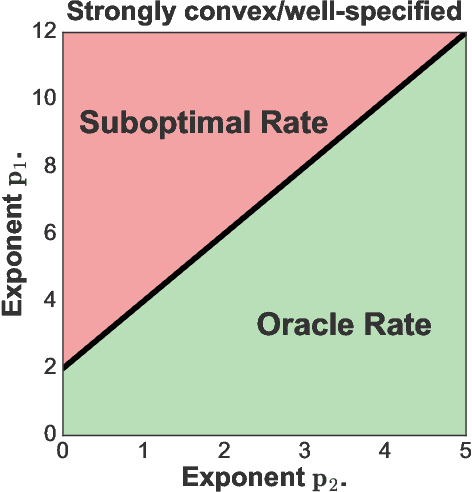
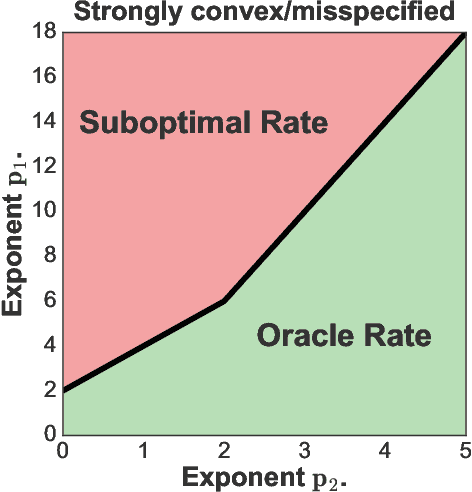
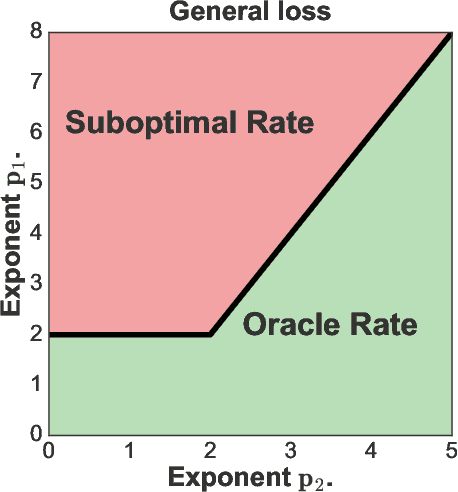
Abstract:We provide excess risk guarantees for statistical learning in the presence of an unknown nuisance component. We analyze a two-stage sample splitting meta-algorithm that takes as input two arbitrary estimation algorithms: one for the target model and one for the nuisance model. We show that if the population risk satisfies a condition called Neyman orthogonality, the impact of the first stage error on the excess risk bound achieved by the meta-algorithm is of second order. Our general theorem is agnostic to the particular algorithms used for the target and nuisance and only makes an assumption on their individual performance. This enables the use of a plethora of existing results from statistical learning and machine learning literature to give new guarantees for learning with a nuisance component. Moreover, by focusing on excess risk rather than parameter estimation, we can give guarantees under weaker assumptions than in previous works and accommodate the case where the target parameter belongs to a complex nonparametric class. When the nuisance and target parameters belong to arbitrary classes, we characterize conditions on the metric entropy such that oracle rates---rates of the same order as if we knew the nuisance model---are achieved. We also analyze the rates achieved by specific estimation algorithms such as variance-penalized empirical risk minimization, neural network estimation and sparse high-dimensional linear model estimation. We highlight the applicability of our results via four applications of primary importance: 1) heterogeneous treatment effect estimation, 2) offline policy optimization, 3) domain adaptation, and 4) learning with missing data.
Non-Parametric Inference Adaptive to Intrinsic Dimension
Jan 11, 2019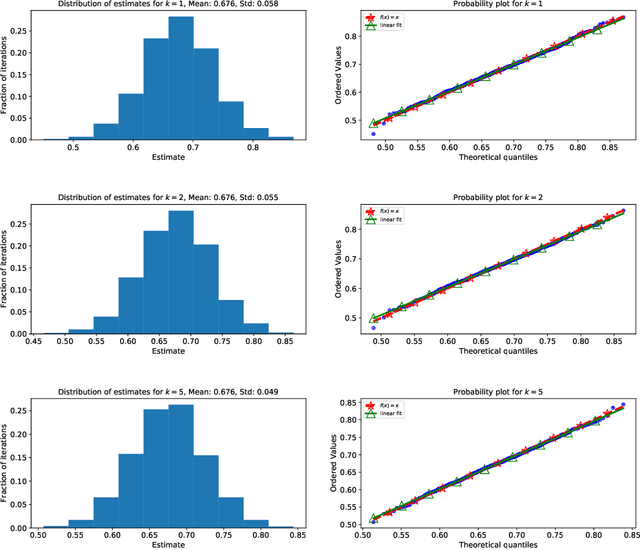
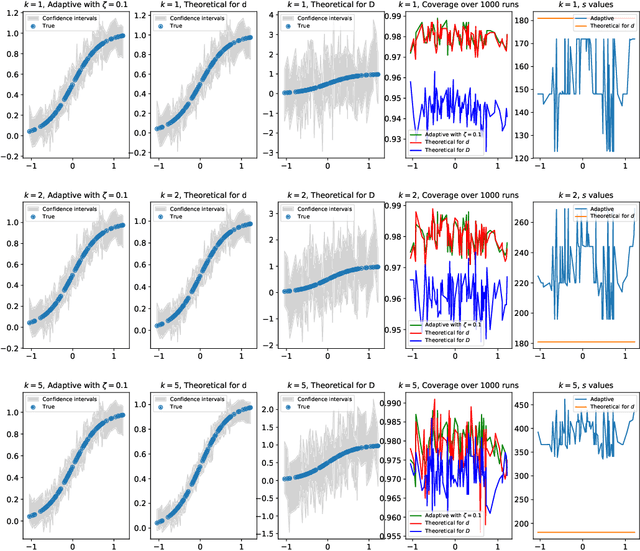
Abstract:We consider non-parametric estimation and inference of conditional moment models in high dimensions. We show that even when the dimension $D$ of the conditioning variable is larger than the sample size $n$, estimation and inference is feasible as long as the distribution of the conditioning variable has small intrinsic dimension $d$, as measured by the doubling dimension. Our estimation is based on a sub-sampled ensemble of the $k$-nearest neighbors $Z$-estimator. We show that if the intrinsic dimension of the co-variate distribution is equal to $d$, then the finite sample estimation error of our estimator is of order $n^{-1/(d+2)}$ and our estimate is $n^{1/(d+2)}$-asymptotically normal, irrespective of $D$. We discuss extensions and applications to heterogeneous treatment effect estimation.
Orthogonal Machine Learning: Power and Limitations
Aug 01, 2018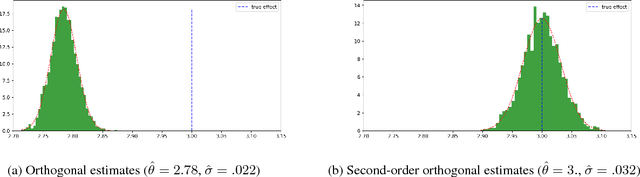
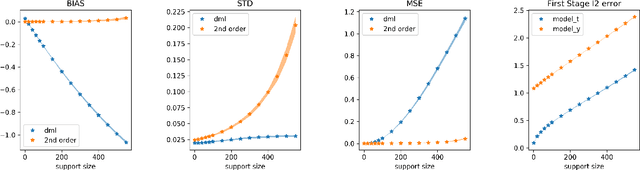
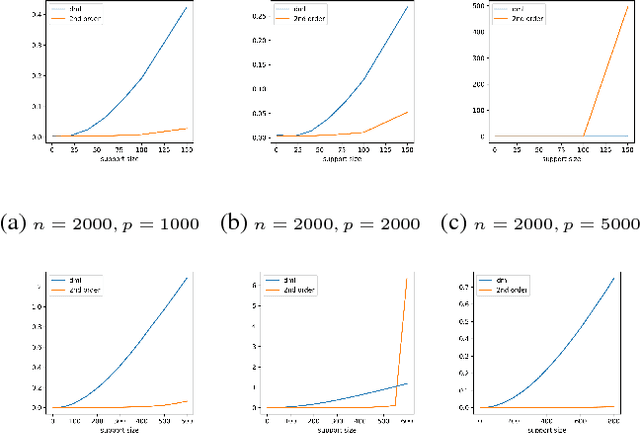
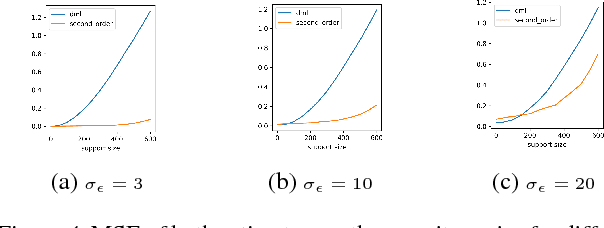
Abstract:Double machine learning provides $\sqrt{n}$-consistent estimates of parameters of interest even when high-dimensional or nonparametric nuisance parameters are estimated at an $n^{-1/4}$ rate. The key is to employ Neyman-orthogonal moment equations which are first-order insensitive to perturbations in the nuisance parameters. We show that the $n^{-1/4}$ requirement can be improved to $n^{-1/(2k+2)}$ by employing a $k$-th order notion of orthogonality that grants robustness to more complex or higher-dimensional nuisance parameters. In the partially linear regression setting popular in causal inference, we show that we can construct second-order orthogonal moments if and only if the treatment residual is not normally distributed. Our proof relies on Stein's lemma and may be of independent interest. We conclude by demonstrating the robustness benefits of an explicit doubly-orthogonal estimation procedure for treatment effect.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge