Varun Kanade
Online Optimization of Smoothed Piecewise Constant Functions
May 20, 2016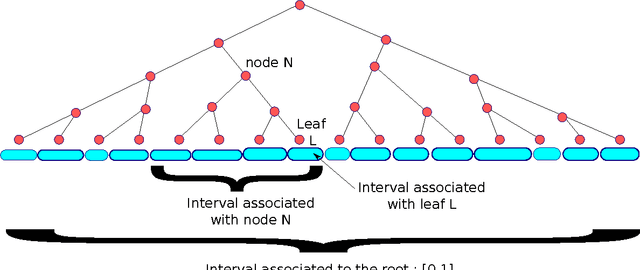
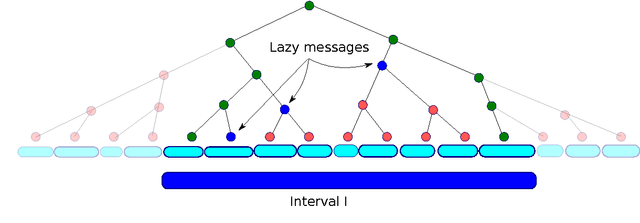
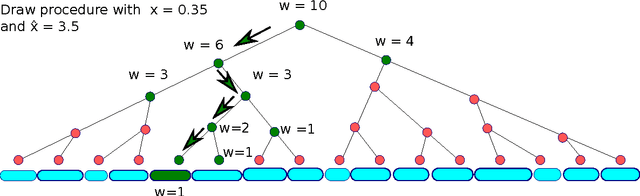
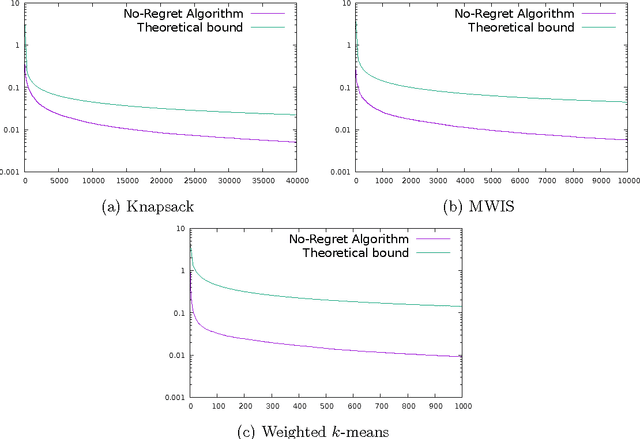
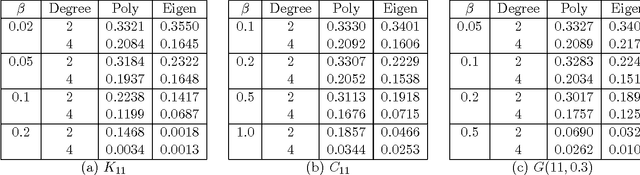
Abstract:We study online optimization of smoothed piecewise constant functions over the domain [0, 1). This is motivated by the problem of adaptively picking parameters of learning algorithms as in the recently introduced framework by Gupta and Roughgarden (2016). Majority of the machine learning literature has focused on Lipschitz-continuous functions or functions with bounded gradients. 1 This is with good reason---any learning algorithm suffers linear regret even against piecewise constant functions that are chosen adversarially, arguably the simplest of non-Lipschitz continuous functions. The smoothed setting we consider is inspired by the seminal work of Spielman and Teng (2004) and the recent work of Gupta and Roughgarden---in this setting, the sequence of functions may be chosen by an adversary, however, with some uncertainty in the location of discontinuities. We give algorithms that achieve sublinear regret in the full information and bandit settings.
MCMC Learning
Jun 12, 2015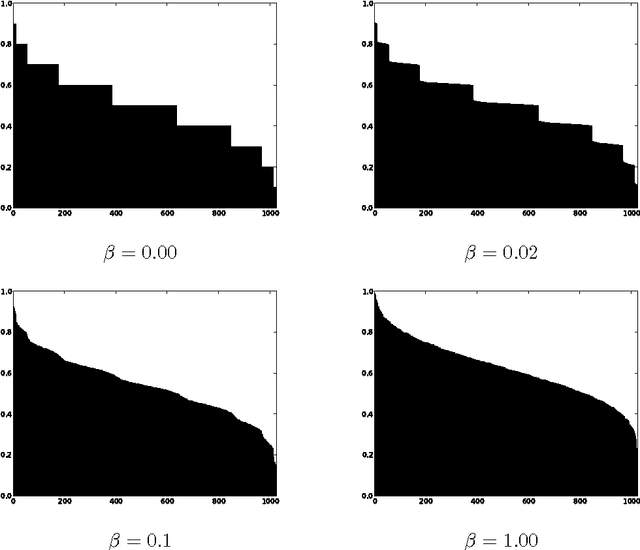


Abstract:The theory of learning under the uniform distribution is rich and deep, with connections to cryptography, computational complexity, and the analysis of boolean functions to name a few areas. This theory however is very limited due to the fact that the uniform distribution and the corresponding Fourier basis are rarely encountered as a statistical model. A family of distributions that vastly generalizes the uniform distribution on the Boolean cube is that of distributions represented by Markov Random Fields (MRF). Markov Random Fields are one of the main tools for modeling high dimensional data in many areas of statistics and machine learning. In this paper we initiate the investigation of extending central ideas, methods and algorithms from the theory of learning under the uniform distribution to the setup of learning concepts given examples from MRF distributions. In particular, our results establish a novel connection between properties of MCMC sampling of MRFs and learning under the MRF distribution.
Learning with a Drifting Target Concept
May 20, 2015Abstract:We study the problem of learning in the presence of a drifting target concept. Specifically, we provide bounds on the error rate at a given time, given a learner with access to a history of independent samples labeled according to a target concept that can change on each round. One of our main contributions is a refinement of the best previous results for polynomial-time algorithms for the space of linear separators under a uniform distribution. We also provide general results for an algorithm capable of adapting to a variable rate of drift of the target concept. Some of the results also describe an active learning variant of this setting, and provide bounds on the number of queries for the labels of points in the sequence sufficient to obtain the stated bounds on the error rates.
Attribute-Efficient Evolvability of Linear Functions
Apr 03, 2014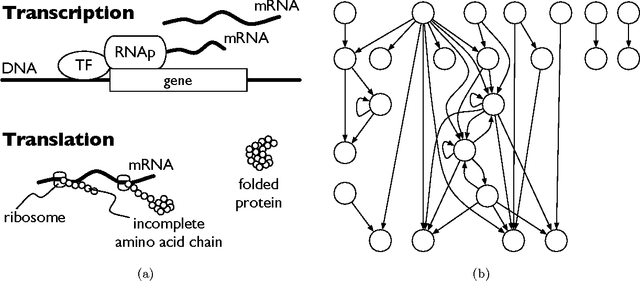
Abstract:In a seminal paper, Valiant (2006) introduced a computational model for evolution to address the question of complexity that can arise through Darwinian mechanisms. Valiant views evolution as a restricted form of computational learning, where the goal is to evolve a hypothesis that is close to the ideal function. Feldman (2008) showed that (correlational) statistical query learning algorithms could be framed as evolutionary mechanisms in Valiant's model. P. Valiant (2012) considered evolvability of real-valued functions and also showed that weak-optimization algorithms that use weak-evaluation oracles could be converted to evolutionary mechanisms. In this work, we focus on the complexity of representations of evolutionary mechanisms. In general, the reductions of Feldman and P. Valiant may result in intermediate representations that are arbitrarily complex (polynomial-sized circuits). We argue that biological constraints often dictate that the representations have low complexity, such as constant depth and fan-in circuits. We give mechanisms for evolving sparse linear functions under a large class of smooth distributions. These evolutionary algorithms are attribute-efficient in the sense that the size of the representations and the number of generations required depend only on the sparsity of the target function and the accuracy parameter, but have no dependence on the total number of attributes.
Distribution-Independent Reliable Learning
Feb 20, 2014
Abstract:We study several questions in the reliable agnostic learning framework of Kalai et al. (2009), which captures learning tasks in which one type of error is costlier than others. A positive reliable classifier is one that makes no false positive errors. The goal in the positive reliable agnostic framework is to output a hypothesis with the following properties: (i) its false positive error rate is at most $\epsilon$, (ii) its false negative error rate is at most $\epsilon$ more than that of the best positive reliable classifier from the class. A closely related notion is fully reliable agnostic learning, which considers partial classifiers that are allowed to predict "unknown" on some inputs. The best fully reliable partial classifier is one that makes no errors and minimizes the probability of predicting "unknown", and the goal in fully reliable learning is to output a hypothesis that is almost as good as the best fully reliable partial classifier from a class. For distribution-independent learning, the best known algorithms for PAC learning typically utilize polynomial threshold representations, while the state of the art agnostic learning algorithms use point-wise polynomial approximations. We show that one-sided polynomial approximations, an intermediate notion between polynomial threshold representations and point-wise polynomial approximations, suffice for learning in the reliable agnostic settings. We then show that majorities can be fully reliably learned and disjunctions of majorities can be positive reliably learned, through constructions of appropriate one-sided polynomial approximations. Our fully reliable algorithm for majorities provides the first evidence that fully reliable learning may be strictly easier than agnostic learning. Our algorithms also satisfy strong attribute-efficiency properties, and provide smooth tradeoffs between sample complexity and running time.
Learning using Local Membership Queries
Apr 17, 2013



Abstract:We introduce a new model of membership query (MQ) learning, where the learning algorithm is restricted to query points that are \emph{close} to random examples drawn from the underlying distribution. The learning model is intermediate between the PAC model (Valiant, 1984) and the PAC+MQ model (where the queries are allowed to be arbitrary points). Membership query algorithms are not popular among machine learning practitioners. Apart from the obvious difficulty of adaptively querying labelers, it has also been observed that querying \emph{unnatural} points leads to increased noise from human labelers (Lang and Baum, 1992). This motivates our study of learning algorithms that make queries that are close to examples generated from the data distribution. We restrict our attention to functions defined on the $n$-dimensional Boolean hypercube and say that a membership query is local if its Hamming distance from some example in the (random) training data is at most $O(\log(n))$. We show the following results in this model: (i) The class of sparse polynomials (with coefficients in R) over $\{0,1\}^n$ is polynomial time learnable under a large class of \emph{locally smooth} distributions using $O(\log(n))$-local queries. This class also includes the class of $O(\log(n))$-depth decision trees. (ii) The class of polynomial-sized decision trees is polynomial time learnable under product distributions using $O(\log(n))$-local queries. (iii) The class of polynomial size DNF formulas is learnable under the uniform distribution using $O(\log(n))$-local queries in time $n^{O(\log(\log(n)))}$. (iv) In addition we prove a number of results relating the proposed model to the traditional PAC model and the PAC+MQ model.
Distributed Non-Stochastic Experts
Nov 14, 2012

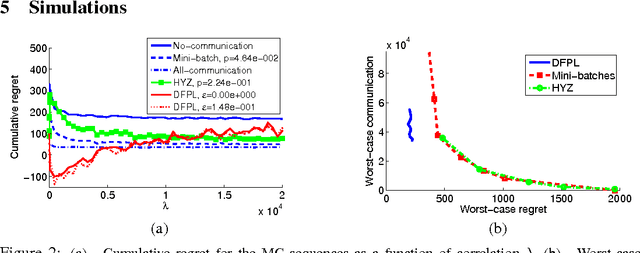
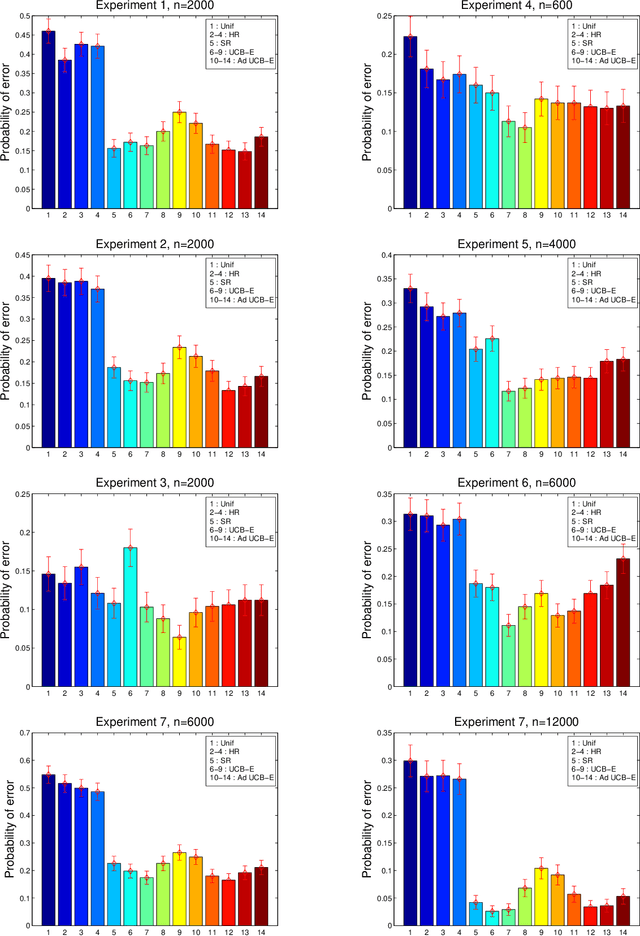
Abstract:We consider the online distributed non-stochastic experts problem, where the distributed system consists of one coordinator node that is connected to $k$ sites, and the sites are required to communicate with each other via the coordinator. At each time-step $t$, one of the $k$ site nodes has to pick an expert from the set ${1, ..., n}$, and the same site receives information about payoffs of all experts for that round. The goal of the distributed system is to minimize regret at time horizon $T$, while simultaneously keeping communication to a minimum. The two extreme solutions to this problem are: (i) Full communication: This essentially simulates the non-distributed setting to obtain the optimal $O(\sqrt{\log(n)T})$ regret bound at the cost of $T$ communication. (ii) No communication: Each site runs an independent copy : the regret is $O(\sqrt{log(n)kT})$ and the communication is 0. This paper shows the difficulty of simultaneously achieving regret asymptotically better than $\sqrt{kT}$ and communication better than $T$. We give a novel algorithm that for an oblivious adversary achieves a non-trivial trade-off: regret $O(\sqrt{k^{5(1+\epsilon)/6} T})$ and communication $O(T/k^{\epsilon})$, for any value of $\epsilon \in (0, 1/5)$. We also consider a variant of the model, where the coordinator picks the expert. In this model, we show that the label-efficient forecaster of Cesa-Bianchi et al. (2005) already gives us strategy that is near optimal in regret vs communication trade-off.
Efficient Learning of Generalized Linear and Single Index Models with Isotonic Regression
Apr 11, 2011


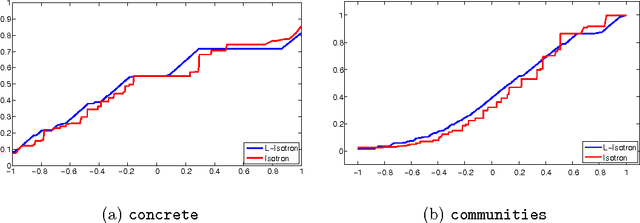
Abstract:Generalized Linear Models (GLMs) and Single Index Models (SIMs) provide powerful generalizations of linear regression, where the target variable is assumed to be a (possibly unknown) 1-dimensional function of a linear predictor. In general, these problems entail non-convex estimation procedures, and, in practice, iterative local search heuristics are often used. Kalai and Sastry (2009) recently provided the first provably efficient method for learning SIMs and GLMs, under the assumptions that the data are in fact generated under a GLM and under certain monotonicity and Lipschitz constraints. However, to obtain provable performance, the method requires a fresh sample every iteration. In this paper, we provide algorithms for learning GLMs and SIMs, which are both computationally and statistically efficient. We also provide an empirical study, demonstrating their feasibility in practice.
Evolution with Drifting Targets
May 19, 2010


Abstract:We consider the question of the stability of evolutionary algorithms to gradual changes, or drift, in the target concept. We define an algorithm to be resistant to drift if, for some inverse polynomial drift rate in the target function, it converges to accuracy 1 -- \epsilon , with polynomial resources, and then stays within that accuracy indefinitely, except with probability \epsilon , at any one time. We show that every evolution algorithm, in the sense of Valiant (2007; 2009), can be converted using the Correlational Query technique of Feldman (2008), into such a drift resistant algorithm. For certain evolutionary algorithms, such as for Boolean conjunctions, we give bounds on the rates of drift that they can resist. We develop some new evolution algorithms that are resistant to significant drift. In particular, we give an algorithm for evolving linear separators over the spherically symmetric distribution that is resistant to a drift rate of O(\epsilon /n), and another algorithm over the more general product normal distributions that resists a smaller drift rate. The above translation result can be also interpreted as one on the robustness of the notion of evolvability itself under changes of definition. As a second result in that direction we show that every evolution algorithm can be converted to a quasi-monotonic one that can evolve from any starting point without the performance ever dipping significantly below that of the starting point. This permits the somewhat unnatural feature of arbitrary performance degradations to be removed from several known robustness translations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge