A Learning Theoretic Perspective on Local Explainability

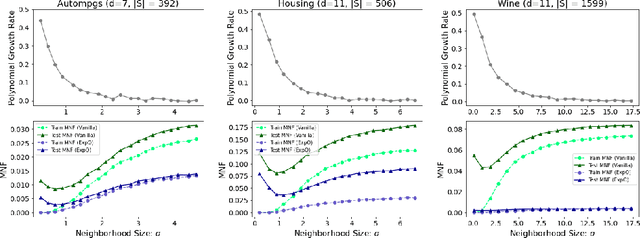
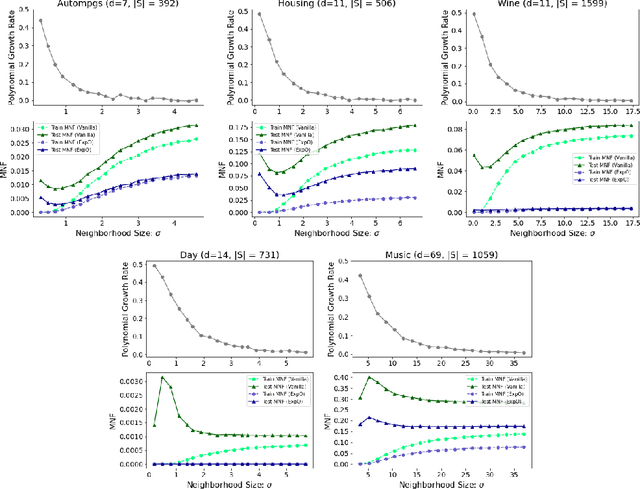
In this paper, we explore connections between interpretable machine learning and learning theory through the lens of local approximation explanations. First, we tackle the traditional problem of performance generalization and bound the test-time accuracy of a model using a notion of how locally explainable it is. Second, we explore the novel problem of explanation generalization which is an important concern for a growing class of finite sample-based local approximation explanations. Finally, we validate our theoretical results empirically and show that they reflect what can be seen in practice.

Understanding the Failure Modes of Out-of-Distribution Generalization

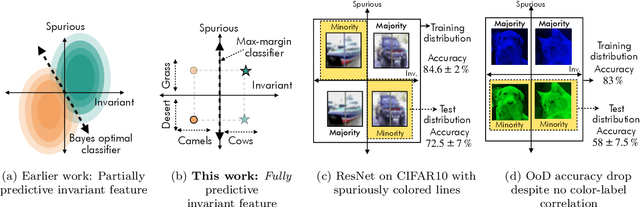
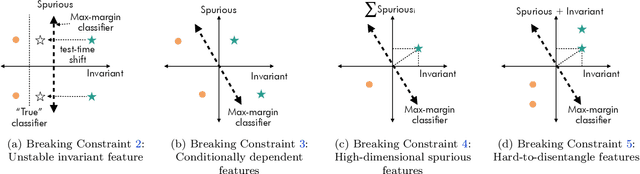
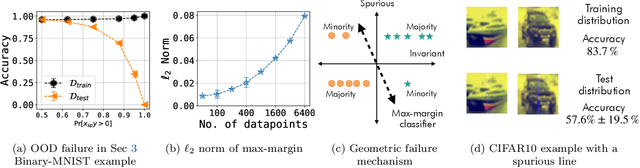
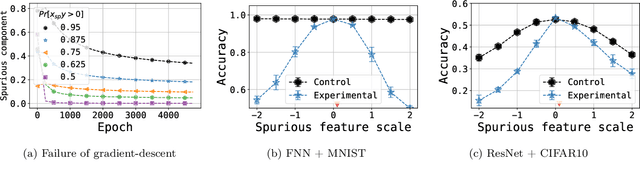
Empirical studies suggest that machine learning models often rely on features, such as the background, that may be spuriously correlated with the label only during training time, resulting in poor accuracy during test-time. In this work, we identify the fundamental factors that give rise to this behavior, by explaining why models fail this way {\em even} in easy-to-learn tasks where one would expect these models to succeed. In particular, through a theoretical study of gradient-descent-trained linear classifiers on some easy-to-learn tasks, we uncover two complementary failure modes. These modes arise from how spurious correlations induce two kinds of skews in the data: one geometric in nature, and another, statistical in nature. Finally, we construct natural modifications of image classification datasets to understand when these failure modes can arise in practice. We also design experiments to isolate the two failure modes when training modern neural networks on these datasets.

Provably Safe PAC-MDP Exploration Using Analogies

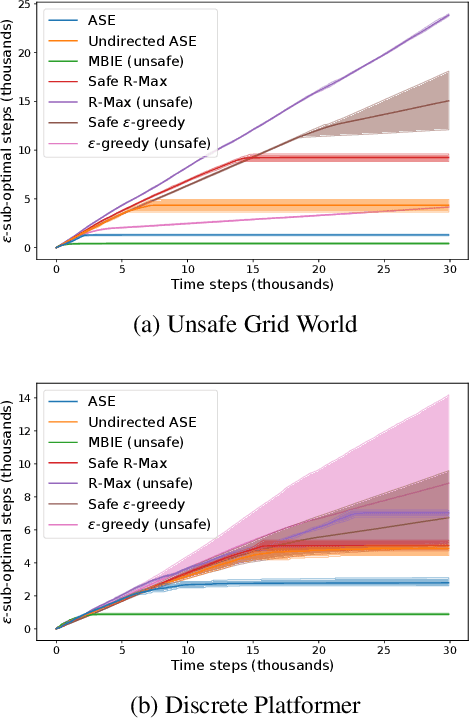
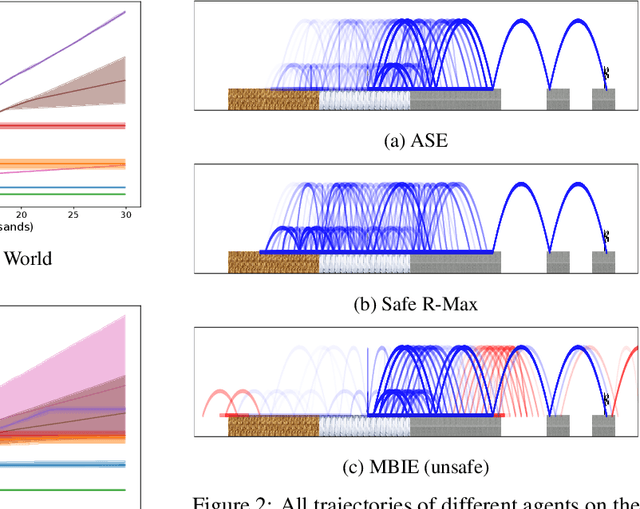
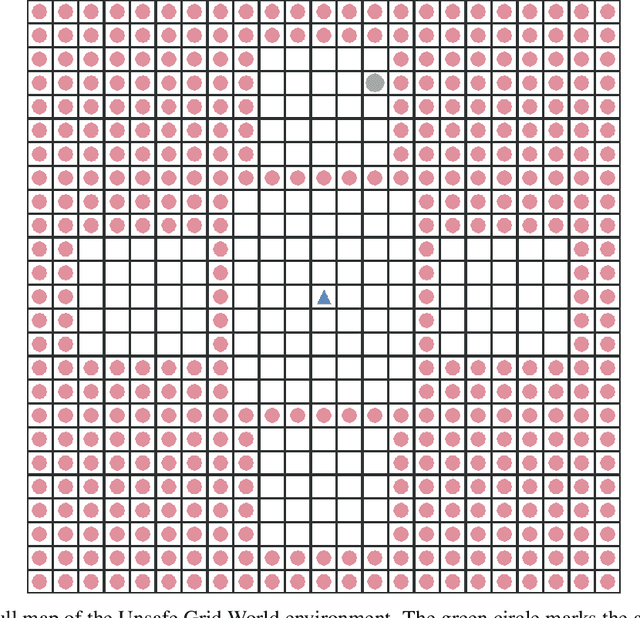
A key challenge in applying reinforcement learning to safety-critical domains is understanding how to balance exploration (needed to attain good performance on the task) with safety (needed to avoid catastrophic failure). Although a growing line of work in reinforcement learning has investigated this area of "safe exploration," most existing techniques either 1) do not guarantee safety during the actual exploration process; and/or 2) limit the problem to a priori known and/or deterministic transition dynamics with strong smoothness assumptions. Addressing this gap, we propose Analogous Safe-state Exploration (ASE), an algorithm for provably safe exploration in MDPs with unknown, stochastic dynamics. Our method exploits analogies between state-action pairs to safely learn a near-optimal policy in a PAC-MDP sense. Additionally, ASE also guides exploration towards the most task-relevant states, which empirically results in significant improvements in terms of sample efficiency, when compared to existing methods.

Deterministic PAC-Bayesian generalization bounds for deep networks via generalizing noise-resilience

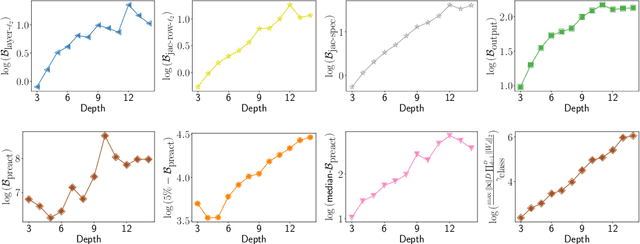
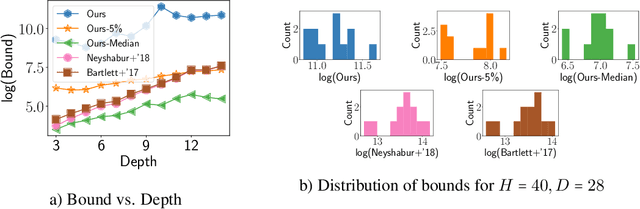
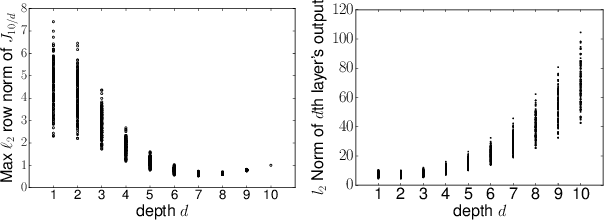
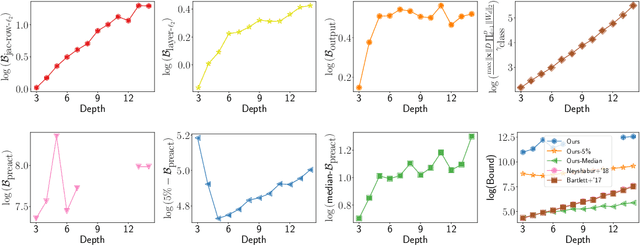
The ability of overparameterized deep networks to generalize well has been linked to the fact that stochastic gradient descent (SGD) finds solutions that lie in flat, wide minima in the training loss -- minima where the output of the network is resilient to small random noise added to its parameters. So far this observation has been used to provide generalization guarantees only for neural networks whose parameters are either \textit{stochastic} or \textit{compressed}. In this work, we present a general PAC-Bayesian framework that leverages this observation to provide a bound on the original network learned -- a network that is deterministic and uncompressed. What enables us to do this is a key novelty in our approach: our framework allows us to show that if on training data, the interactions between the weight matrices satisfy certain conditions that imply a wide training loss minimum, these conditions themselves {\em generalize} to the interactions between the matrices on test data, thereby implying a wide test loss minimum. We then apply our general framework in a setup where we assume that the pre-activation values of the network are not too small (although we assume this only on the training data). In this setup, we provide a generalization guarantee for the original (deterministic, uncompressed) network, that does not scale with product of the spectral norms of the weight matrices -- a guarantee that would not have been possible with prior approaches.

Uniform convergence may be unable to explain generalization in deep learning

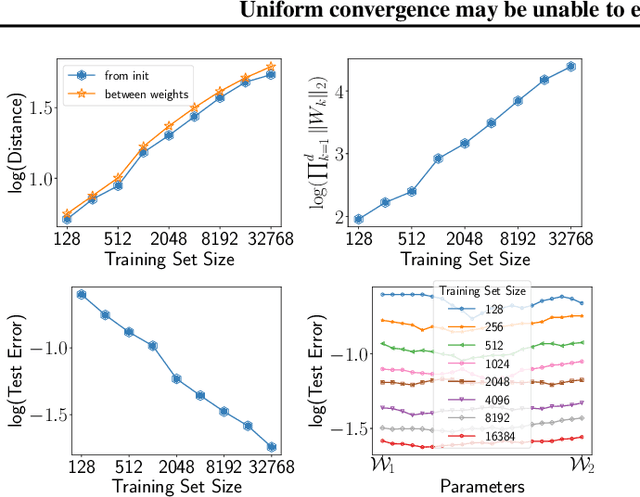
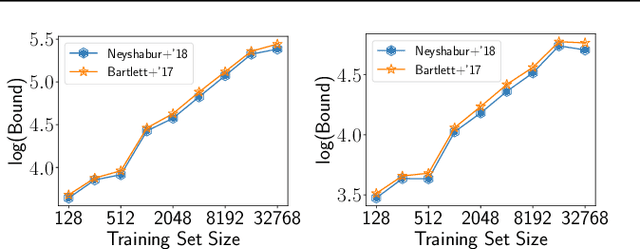
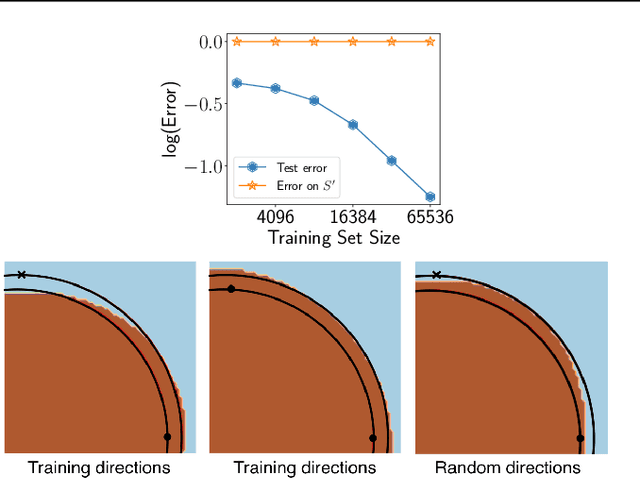
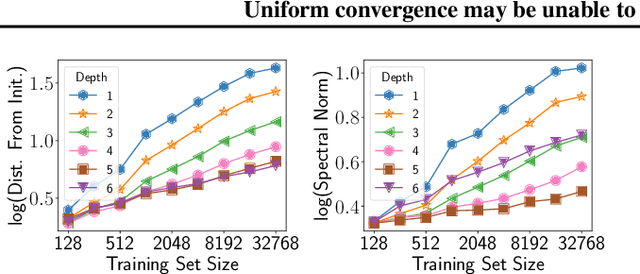
We cast doubt on the power of uniform convergence-based generalization bounds to provide a complete picture of why overparameterized deep networks generalize well. While it is well-known that many existing bounds are numerically large, through a variety of experiments, we first bring to light another crucial and more concerning aspect of these bounds: in practice, these bounds can {\em increase} with the dataset size. Guided by our observations, we then present examples of overparameterized linear classifiers and neural networks trained by stochastic gradient descent (SGD) where uniform convergence provably cannot `explain generalization,' even if we take into account implicit regularization {\em to the fullest extent possible}. More precisely, even if we consider only the set of classifiers output by SGD that have test errors less than some small $\epsilon$, applying (two-sided) uniform convergence on this set of classifiers yields a generalization guarantee that is larger than $1-\epsilon$ and is therefore nearly vacuous.

Generalization in Deep Networks: The Role of Distance from Initialization

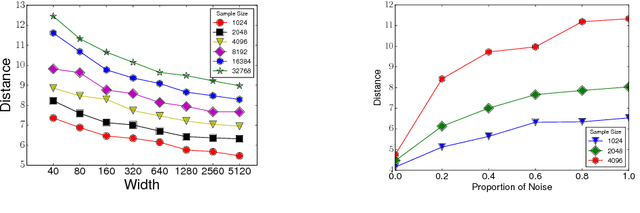
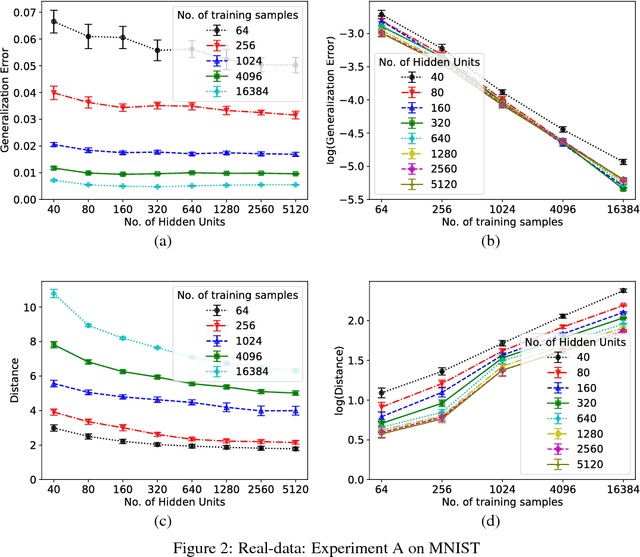
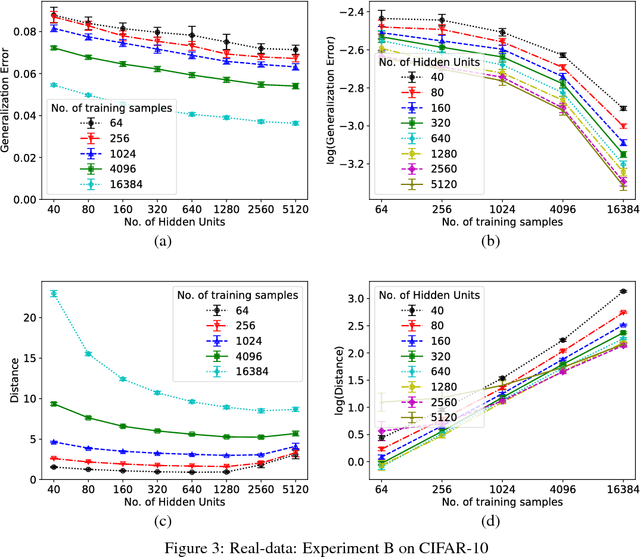
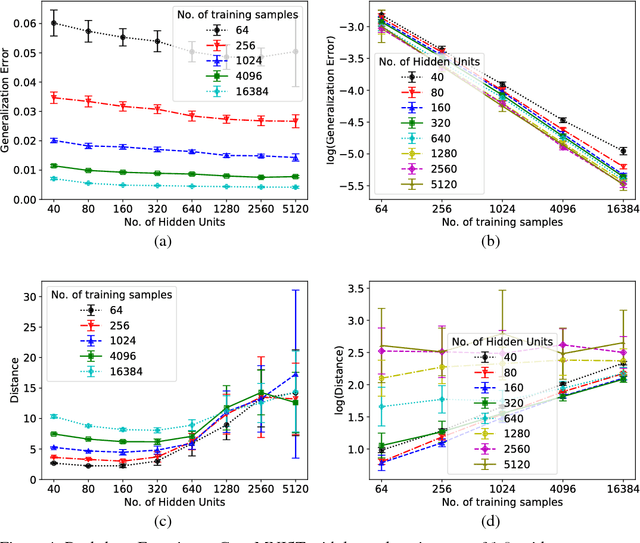
Why does training deep neural networks using stochastic gradient descent (SGD) result in a generalization error that does not worsen with the number of parameters in the network? To answer this question, we advocate a notion of effective model capacity that is dependent on {\em a given random initialization of the network} and not just the training algorithm and the data distribution. We provide empirical evidences that demonstrate that the model capacity of SGD-trained deep networks is in fact restricted through implicit regularization of {\em the $\ell_2$ distance from the initialization}. We also provide theoretical arguments that further highlight the need for initialization-dependent notions of model capacity. We leave as open questions how and why distance from initialization is regularized, and whether it is sufficient to explain generalization.

Learning-Theoretic Foundations of Algorithm Configuration for Combinatorial Partitioning Problems

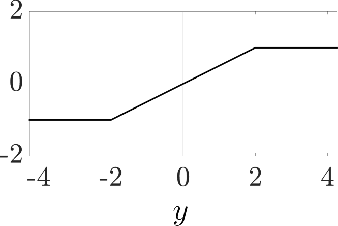
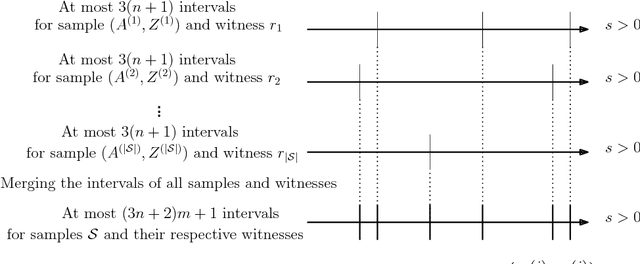
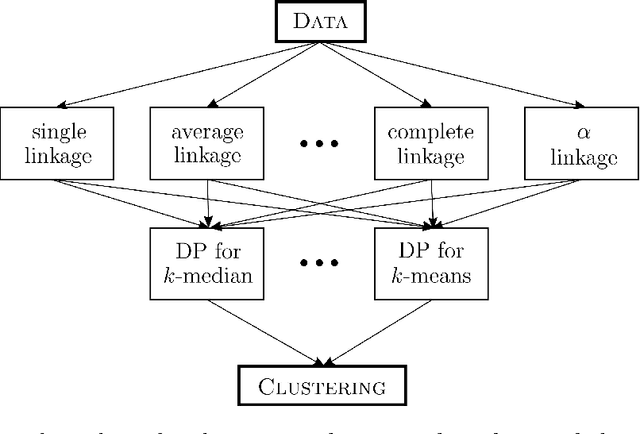
Max-cut, clustering, and many other partitioning problems that are of significant importance to machine learning and other scientific fields are NP-hard, a reality that has motivated researchers to develop a wealth of approximation algorithms and heuristics. Although the best algorithm to use typically depends on the specific application domain, a worst-case analysis is often used to compare algorithms. This may be misleading if worst-case instances occur infrequently, and thus there is a demand for optimization methods which return the algorithm configuration best suited for the given application's typical inputs. We address this problem for clustering, max-cut, and other partitioning problems, such as integer quadratic programming, by designing computationally efficient and sample efficient learning algorithms which receive samples from an application-specific distribution over problem instances and learn a partitioning algorithm with high expected performance. Our algorithms learn over common integer quadratic programming and clustering algorithm families: SDP rounding algorithms and agglomerative clustering algorithms with dynamic programming. For our sample complexity analysis, we provide tight bounds on the pseudodimension of these algorithm classes, and show that surprisingly, even for classes of algorithms parameterized by a single parameter, the pseudo-dimension is superconstant. In this way, our work both contributes to the foundations of algorithm configuration and pushes the boundaries of learning theory, since the algorithm classes we analyze consist of multi-stage optimization procedures and are significantly more complex than classes typically studied in learning theory.

On Adversarial Risk and Training

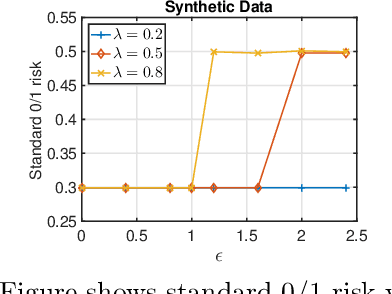
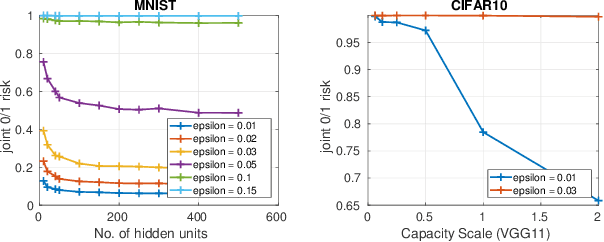
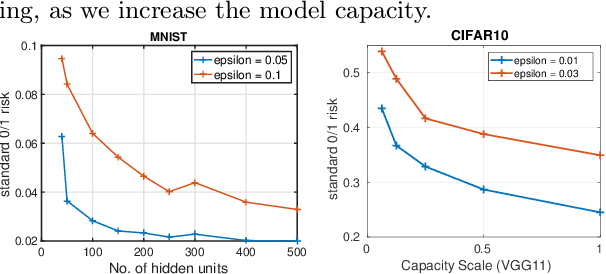
In this work we formally define the notions of adversarial perturbations, adversarial risk and adversarial training and analyze their properties. Our analysis provides several interesting insights into adversarial risk, adversarial training, and their relation to the classification risk, "traditional" training. We also show that adversarial training can result in models with better classification accuracy and can result in better explainable models than traditional training. Although adversarial training is computationally expensive, our results and insights suggest that one should prefer adversarial training over traditional risk minimization for learning complex models from data.

Gradient descent GAN optimization is locally stable

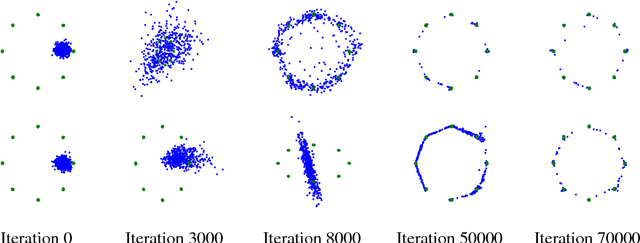
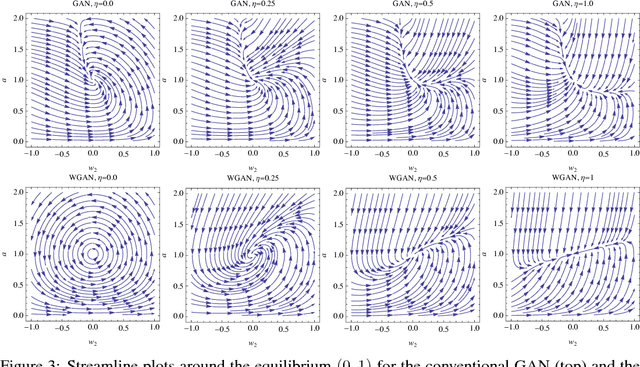
Despite the growing prominence of generative adversarial networks (GANs), optimization in GANs is still a poorly understood topic. In this paper, we analyze the "gradient descent" form of GAN optimization i.e., the natural setting where we simultaneously take small gradient steps in both generator and discriminator parameters. We show that even though GAN optimization does not correspond to a convex-concave game (even for simple parameterizations), under proper conditions, equilibrium points of this optimization procedure are still \emph{locally asymptotically stable} for the traditional GAN formulation. On the other hand, we show that the recently proposed Wasserstein GAN can have non-convergent limit cycles near equilibrium. Motivated by this stability analysis, we propose an additional regularization term for gradient descent GAN updates, which \emph{is} able to guarantee local stability for both the WGAN and the traditional GAN, and also shows practical promise in speeding up convergence and addressing mode collapse.

Lifelong Learning in Costly Feature Spaces

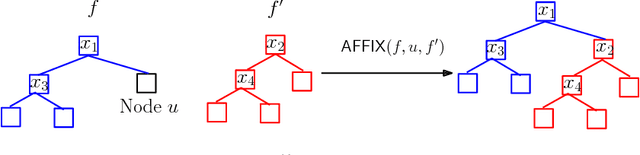
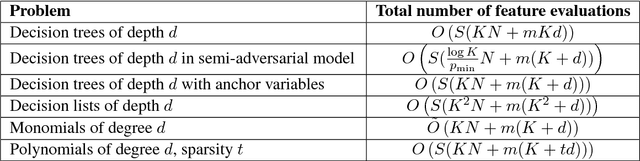
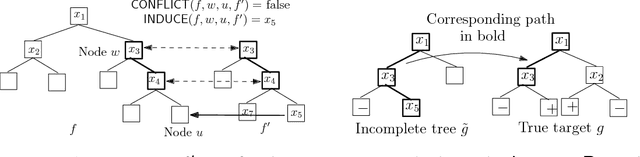
An important long-term goal in machine learning systems is to build learning agents that, like humans, can learn many tasks over their lifetime, and moreover use information from these tasks to improve their ability to do so efficiently. In this work, our goal is to provide new theoretical insights into the potential of this paradigm. In particular, we propose a lifelong learning framework that adheres to a novel notion of resource efficiency that is critical in many real-world domains where feature evaluations are costly. That is, our learner aims to reuse information from previously learned related tasks to learn future tasks in a feature-efficient manner. Furthermore, we consider novel combinatorial ways in which learning tasks can relate. Specifically, we design lifelong learning algorithms for two structurally different and widely used families of target functions: decision trees/lists and monomials/polynomials. We also provide strong feature-efficiency guarantees for these algorithms; in fact, we show that in order to learn future targets, we need only slightly more feature evaluations per training example than what is needed to predict on an arbitrary example using those targets. We also provide algorithms with guarantees in an agnostic model where not all the targets are related to each other. Finally, we also provide lower bounds on the performance of a lifelong learner in these models, which are in fact tight under some conditions.