Horseshoe Mixtures-of-Experts (HS-MoE)

Horseshoe mixtures-of-experts (HS-MoE) models provide a Bayesian framework for sparse expert selection in mixture-of-experts architectures. We combine the horseshoe prior's adaptive global-local shrinkage with input-dependent gating, yielding data-adaptive sparsity in expert usage. Our primary methodological contribution is a particle learning algorithm for sequential inference, in which the filter is propagated forward in time while tracking only sufficient statistics. We also discuss how HS-MoE relates to modern mixture-of-experts layers in large language models, which are deployed under extreme sparsity constraints (e.g., activating a small number of experts per token out of a large pool).

Generative Bayesian Hyperparameter Tuning

\noindent Hyper-parameter selection is a central practical problem in modern machine learning, governing regularization strength, model capacity, and robustness choices. Cross-validation is often computationally prohibitive at scale, while fully Bayesian hyper-parameter learning can be difficult due to the cost of posterior sampling. We develop a generative perspective on hyper-parameter tuning that combines two ideas: (i) optimization-based approximations to Bayesian posteriors via randomized, weighted objectives (weighted Bayesian bootstrap), and (ii) amortization of repeated optimization across many hyper-parameter settings by learning a transport map from hyper-parameters (including random weights) to the corresponding optimizer. This yields a ``generator look-up table'' for estimators, enabling rapid evaluation over grids or continuous ranges of hyper-parameters and supporting both predictive tuning objectives and approximate Bayesian uncertainty quantification. We connect this viewpoint to weighted $M$-estimation, envelope/auxiliary-variable representations that reduce non-quadratic losses to weighted least squares, and recent generative samplers for weighted $M$-estimators.

Bayesian Double Descent

Double descent is a phenomenon of over-parameterized statistical models. Our goal is to view double descent from a Bayesian perspective. Over-parameterized models such as deep neural networks have an interesting re-descending property in their risk characteristics. This is a recent phenomenon in machine learning and has been the subject of many studies. As the complexity of the model increases, there is a U-shaped region corresponding to the traditional bias-variance trade-off, but then as the number of parameters equals the number of observations and the model becomes one of interpolation, the risk can become infinite and then, in the over-parameterized region, it re-descends -- the double descent effect. We show that this has a natural Bayesian interpretation. Moreover, we show that it is not in conflict with the traditional Occam's razor that Bayesian models possess, in that they tend to prefer simpler models when possible. We illustrate the approach with an example of Bayesian model selection in neural networks. Finally, we conclude with directions for future research.

Kolmogorov GAM Networks are all you need!

Kolmogorov GAM (K-GAM) networks are shown to be an efficient architecture for training and inference. They are an additive model with an embedding that is independent of the function of interest. They provide an alternative to the transformer architecture. They are the machine learning version of Kolmogorov's Superposition Theorem (KST) which provides an efficient representations of a multivariate function. Such representations have use in machine learning for encoding dictionaries (a.k.a. "look-up" tables). KST theory also provides a representation based on translates of the K\"oppen function. The goal of our paper is to interpret this representation in a machine learning context for applications in Artificial Intelligence (AI). Our architecture is equivalent to a topological embedding which is independent of the function together with an additive layer that uses a Generalized Additive Model (GAM). This provides a class of learning procedures with far fewer parameters than current deep learning algorithms. Implementation can be parallelizable which makes our algorithms computationally attractive. To illustrate our methodology, we use the Iris data from statistical learning. We also show that our additive model with non-linear embedding provides an alternative to transformer architectures which from a statistical viewpoint are kernel smoothers. Additive KAN models therefore provide a natural alternative to transformers. Finally, we conclude with directions for future research.

Generative Bayesian Computation for Maximum Expected Utility

Generative Bayesian Computation (GBC) methods are developed to provide an efficient computational solution for maximum expected utility (MEU). We propose a density-free generative method based on quantiles that naturally calculates expected utility as a marginal of quantiles. Our approach uses a deep quantile neural estimator to directly estimate distributional utilities. Generative methods assume only the ability to simulate from the model and parameters and as such are likelihood-free. A large training dataset is generated from parameters and output together with a base distribution. Our method a number of computational advantages primarily being density-free with an efficient estimator of expected utility. A link with the dual theory of expected utility and risk taking is also discussed. To illustrate our methodology, we solve an optimal portfolio allocation problem with Bayesian learning and a power utility (a.k.a. fractional Kelly criterion). Finally, we conclude with directions for future research.

Deep Learning: A Tutorial

Our goal is to provide a review of deep learning methods which provide insight into structured high-dimensional data. Rather than using shallow additive architectures common to most statistical models, deep learning uses layers of semi-affine input transformations to provide a predictive rule. Applying these layers of transformations leads to a set of attributes (or, features) to which probabilistic statistical methods can be applied. Thus, the best of both worlds can be achieved: scalable prediction rules fortified with uncertainty quantification, where sparse regularization finds the features.

The Value of Chess Squares

Valuing chess squares and determining the placement of pieces on the board are the main objectives of our study. With the emergence of chess AI, it has become possible to accurately assess the worth of positions in a game of chess. The conventional approach assigns fixed values to pieces $(\symking=\infty, \symqueen=9, \symrook=5, \symbishop=3, \symknight=3, \sympawn=1)$. We enhance this analysis by introducing marginal valuations for both pieces and squares. We demonstrate our method by examining the positioning of Knights and Bishops, and also provide valuable insights into the valuation of pawns. Notably, Nimzowitsch was among the pioneers in advocating for the significance of Pawn structure and valuation. Finally, we conclude by suggesting potential avenues for future research.

Quantum Bayes AI

Quantum Bayesian AI (Q-B) is an emerging field that levers the computational gains available in Quantum computing. The promise is an exponential speed-up in many Bayesian algorithms. Our goal is to apply these methods directly to statistical and machine learning problems. We provide a duality between classical and quantum probability for calculating of posterior quantities of interest. Our framework unifies MCMC, Deep Learning and Quantum Learning calculations from the viewpoint from von Neumann's principle of quantum measurement. Quantum embeddings and neural gates are also an important part of data encoding and feature selection. There is a natural duality with well-known kernel methods in statistical learning. We illustrate the behaviour of quantum algorithms on two simple classification algorithms. Finally, we conclude with directions for future research.

Bayesian Calibration for Activity Based Models

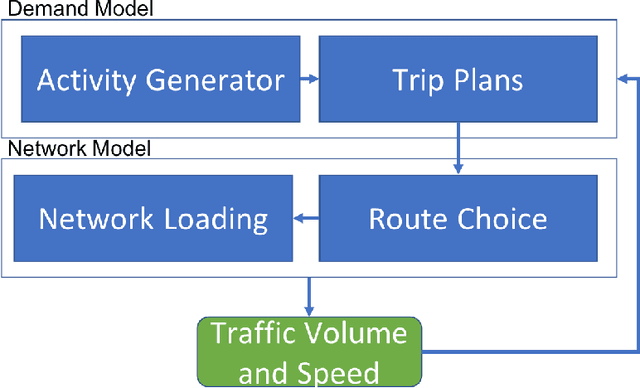
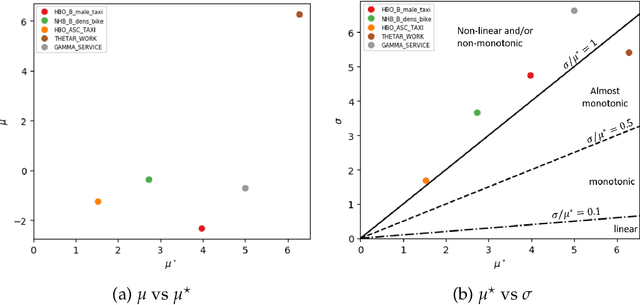
We consider the problem of calibration and uncertainty analysis for activity-based transportation simulators. ABMs rely on statistical models of traveler's behavior to predict travel patterns in a metropolitan area. Input parameters are typically estimated from traveler's surveys using maximum likelihood. We develop an approach that uses Gaussian process emulator to calibrate an activity-based model of a metropolitan transplantation system. Our approach extends traditional emulators to handle high-dimensional and non-stationary nature of the transportation simulator. Our methodology is applied to transportation simulator of Bloomington, Illinois. We calibrate key parameters of the model and compare to the ad-hoc calibration process.

Deep Generative Models for Vehicle Speed Trajectories

Generating realistic vehicle speed trajectories is a crucial component in evaluating vehicle fuel economy and in predictive control of self-driving cars. Traditional generative models rely on Markov chain methods and can produce accurate synthetic trajectories but are subject to the curse of dimensionality. They do not allow to include conditional input variables into the generation process. In this paper, we show how extensions to deep generative models allow accurate and scalable generation. Proposed architectures involve recurrent and feed-forward layers and are trained using adversarial techniques. Our models are shown to perform well on generating vehicle trajectories using a model trained on GPS data from Chicago metropolitan area.