Generative Bayesian Hyperparameter Tuning

\noindent Hyper-parameter selection is a central practical problem in modern machine learning, governing regularization strength, model capacity, and robustness choices. Cross-validation is often computationally prohibitive at scale, while fully Bayesian hyper-parameter learning can be difficult due to the cost of posterior sampling. We develop a generative perspective on hyper-parameter tuning that combines two ideas: (i) optimization-based approximations to Bayesian posteriors via randomized, weighted objectives (weighted Bayesian bootstrap), and (ii) amortization of repeated optimization across many hyper-parameter settings by learning a transport map from hyper-parameters (including random weights) to the corresponding optimizer. This yields a ``generator look-up table'' for estimators, enabling rapid evaluation over grids or continuous ranges of hyper-parameters and supporting both predictive tuning objectives and approximate Bayesian uncertainty quantification. We connect this viewpoint to weighted $M$-estimation, envelope/auxiliary-variable representations that reduce non-quadratic losses to weighted least squares, and recent generative samplers for weighted $M$-estimators.

Efficient sampling for Gaussian linear regression with arbitrary priors

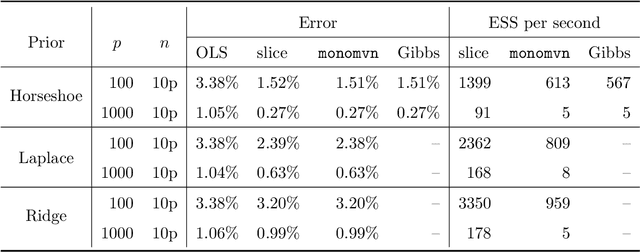
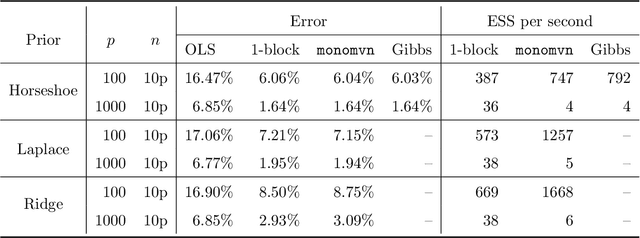
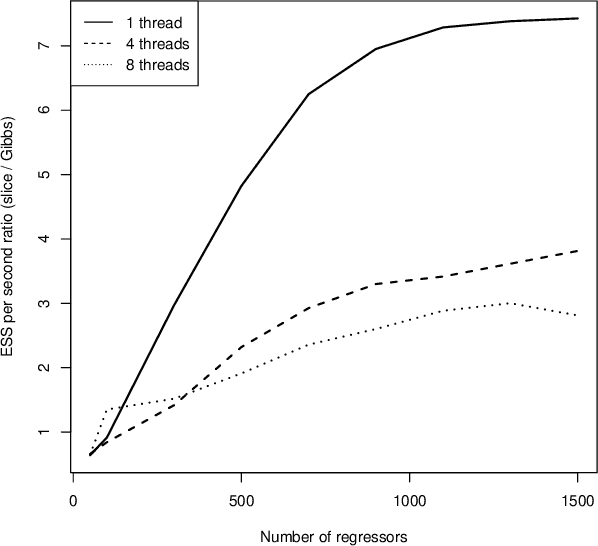
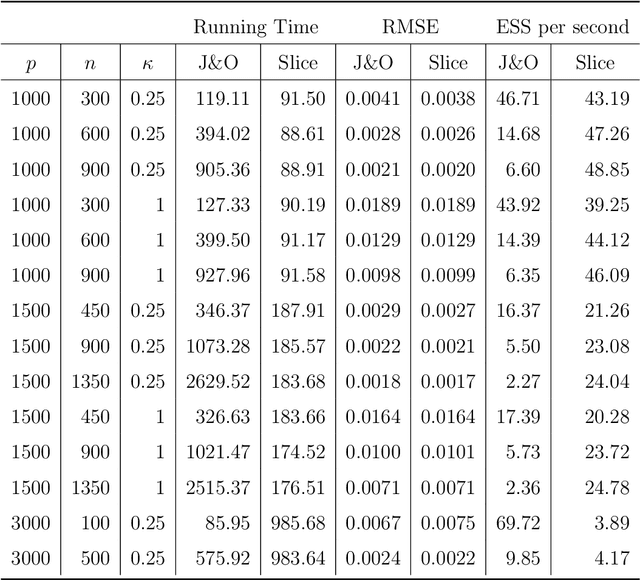
This paper develops a slice sampler for Bayesian linear regression models with arbitrary priors. The new sampler has two advantages over current approaches. One, it is faster than many custom implementations that rely on auxiliary latent variables, if the number of regressors is large. Two, it can be used with any prior with a density function that can be evaluated up to a normalizing constant, making it ideal for investigating the properties of new shrinkage priors without having to develop custom sampling algorithms. The new sampler takes advantage of the special structure of the linear regression likelihood, allowing it to produce better effective sample size per second than common alternative approaches.