A-TPT: Angular Diversity Calibration Properties for Test-Time Prompt Tuning of Vision-Language Models

Test-time prompt tuning (TPT) has emerged as a promising technique for adapting large vision-language models (VLMs) to unseen tasks without relying on labeled data. However, the lack of dispersion between textual features can hurt calibration performance, which raises concerns about VLMs' reliability, trustworthiness, and safety. Current TPT approaches primarily focus on improving prompt calibration by either maximizing average textual feature dispersion or enforcing orthogonality constraints to encourage angular separation. However, these methods may not always have optimal angular separation between class-wise textual features, which implies overlooking the critical role of angular diversity. To address this, we propose A-TPT, a novel TPT framework that introduces angular diversity to encourage uniformity in the distribution of normalized textual features induced by corresponding learnable prompts. This uniformity is achieved by maximizing the minimum pairwise angular distance between features on the unit hypersphere. We show that our approach consistently surpasses state-of-the-art TPT methods in reducing the aggregate average calibration error while maintaining comparable accuracy through extensive experiments with various backbones on different datasets. Notably, our approach exhibits superior zero-shot calibration performance on natural distribution shifts and generalizes well to medical datasets. We provide extensive analyses, including theoretical aspects, to establish the grounding of A-TPT. These results highlight the potency of promoting angular diversity to achieve well-dispersed textual features, significantly improving VLM calibration during test-time adaptation. Our code will be made publicly available.

Resilient Sparse Array Radar with the Aid of Deep Learning

In this paper, we address the problem of direction of arrival (DOA) estimation for multiple targets in the presence of sensor failures in a sparse array. Generally, sparse arrays are known with very high-resolution capabilities, where N physical sensors can resolve up to $\mathcal{O}(N^2)$ uncorrelated sources. However, among the many configurations introduced in the literature, the arrays that provide the largest hole-free co-array are the most susceptible to sensor failures. We propose here two machine learning (ML) methods to mitigate the effect of sensor failures and maintain the DOA estimation performance and resolution. The first method enhances the conventional spatial smoothing using deep neural network (DNN), while the second one is an end-to-end data-driven method. Numerical results show that both approaches can significantly improve the performance of MRA with two failed sensors. The data-driven method can maintain the performance of the array with no failures at high signal-tonoise ratio (SNR). Moreover, both approaches can even perform better than the original array at low SNR thanks to the denoising effect of the proposed DNN

Deep Unfolding of Iteratively Reweighted ADMM for Wireless RF Sensing

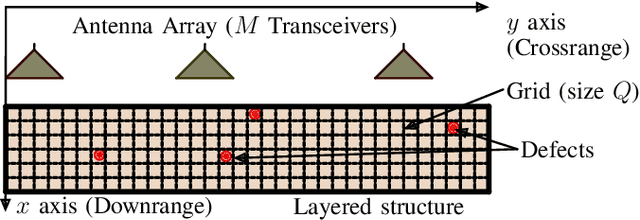
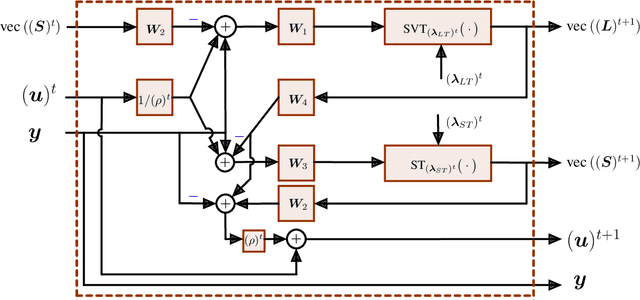
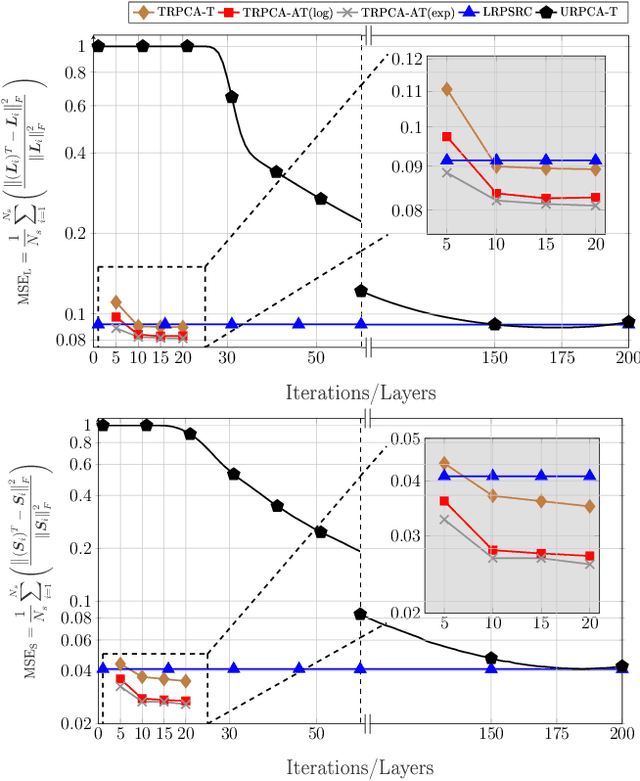
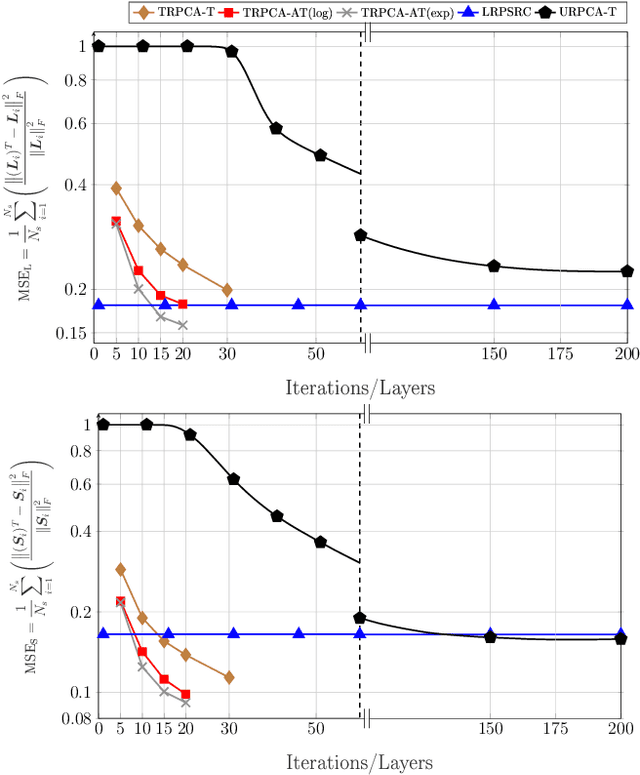
We address the detection of material defects, which are inside a layered material structure using compressive sensing based multiple-output (MIMO) wireless radar. Here, the strong clutter due to the reflection of the layered structure's surface often makes the detection of the defects challenging. Thus, sophisticated signal separation methods are required for improved defect detection. In many scenarios, the number of defects that we are interested in is limited and the signaling response of the layered structure can be modeled as a low-rank structure. Therefore, we propose joint rank and sparsity minimization for defect detection. In particular, we propose a non-convex approach based on the iteratively reweighted nuclear and $\ell_1-$norm (a double-reweighted approach) to obtain a higher accuracy compared to the conventional nuclear norm and $\ell_1-$norm minimization. To this end, an iterative algorithm is designed to estimate the low-rank and sparse contributions. Further, we propose deep learning to learn the parameters of the algorithm (i.e., algorithm unfolding) to improve the accuracy and the speed of convergence of the algorithm. Our numerical results show that the proposed approach outperforms the conventional approaches in terms of mean square errors of the recovered low-rank and sparse components and the speed of convergence.